Vantieghems Theorem for Primality Test
Last Updated :
23 Aug, 2022
Vantieghems Theorem is a necessary and sufficient condition for a number to be prime. It states that for a natural number n to be prime, the product of 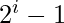 where
where 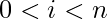 , is congruent to
, is congruent to 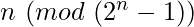 .
.
In other words, a number n is prime if and only if.
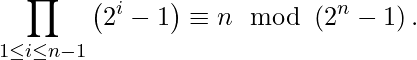
Examples:
- For n = 3, final product is (21 – 1) * (22 – 1) = 1*3 = 3. 3 is congruent to 3 mod 7. We get 3 mod 7 from expression 3 * (mod (23 – 1)), therefore 3 is prime.
- For n = 5, final product is 1*3*7*15 = 315. 315 is congruent to 5(mod 31), therefore 5 is prime.
- For n = 7, final product is 1*3*7*15*31*63 = 615195. 615195 is congruent to 7(mod 127), therefore 7 is prime.
- For n = 4, final product 1*3*7 = 21. 21 is not congruent to 4(mod 15), therefore 4 is composite.
Another way to state above theorem is, if 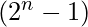 divides
divides 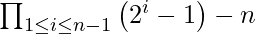 , then n is prime.
, then n is prime.
C++
#include <bits/stdc++.h>
using namespace std;
void checkVantieghemsTheorem(int limit)
{
long long unsigned prod = 1;
for (long long unsigned n = 2; n < limit; n++) {
if (((prod - n) % ((1LL << n) - 1)) == 0)
cout << n << " is prime\n";
prod *= ((1LL << n) - 1);
}
}
int main()
{
checkVantieghemsTheorem(10);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void checkVantieghemsTheorem(int limit)
{
long prod = 1;
for (long n = 2; n < limit; n++)
{
if (((prod - n < 0 ? 0 : prod - n) % ((1 << n) - 1)) == 0)
System.out.print(n + " is prime\n");
prod *= ((1 << n) - 1);
}
}
public static void main(String []args)
{
checkVantieghemsTheorem(10);
}
}
|
Python3
def checkVantieghemsTheorem(limit):
prod = 1
for n in range(2, limit):
if n == 2:
print(2, "is prime")
if (((prod - n) % ((1 << n) - 1)) == 0):
print(n, "is prime")
prod *= ((1 << n) - 1)
checkVantieghemsTheorem(10)
|
C#
using System;
class GFG
{
static void checkVantieghemsTheorem(int limit)
{
long prod = 1;
for (long n = 2; n < limit; n++)
{
if (((prod - n < 0 ? 0 : prod - n) % ((1 << (int)n) - 1)) == 0)
Console.Write(n + " is prime\n");
prod *= ((1 << (int)n) - 1);
}
}
public static void Main()
{
checkVantieghemsTheorem(10);
}
}
|
Javascript
<script>
function checkVantieghemsTheorem( limit)
{
let prod = 1;
for (let n = 2; n < limit; n++) {
if (n == 2)
document.write(2 + " is prime" + "</br>");
if (((prod - n) % ((1 << n) - 1)) == 0)
document.write( n + " is prime" + "</br>");
prod *= ((1 << n) - 1);
}
}
checkVantieghemsTheorem(10);
</script>
|
Output: 2 is prime
3 is prime
5 is prime
7 is prime
Time Complexity : O(limit)
Auxiliary Space: O(1)
The above code does not work for values of n higher than 11. It causes overflow in prod evaluation.
Share your thoughts in the comments
Please Login to comment...