Lucas Primality Test
Last Updated :
29 Jul, 2022
A number p greater than one is prime if and only if the only divisors of p are 1 and p. First few prime numbers are 2, 3, 5, 7, 11, 13, …
The Lucas test is a primality test for a natural number n, it can test primality of any kind of number.
It follows from Fermat’s Little Theorem: If p is prime and a is an integer, then a^p is congruent to a (mod p )
Lucas’ Test : A positive number n
is prime if there exists an integer a (1 < a < n) such that :
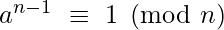
And for every prime factor q of (n-1),

Examples :
Input : n = 7
Output : 7 is Prime
Explanation : let's take a = 3,
then 3^6 % 7 = 729 % 7 = 1 (1st
condition satisfied). Prime factors
of 6 are 2 and 3,
3^(6/2) % 7 = 3^3 % 7 = 27 % 7 = 6
3^(6/3) % 7 = 3^2 % 7 = 9 % 7 = 2
Hence, 7 is Prime
Input : n = 9
Output : 9 is composite
Explanation : Let's take a = 2,
then 2^8 % 9 = 256 % 9 = 4
Hence 9 is composite
lucasTest(n):
If n is even
return composite
Else
Find all prime factors of n-1
for i=2 to n-1
pick 'a' randomly in range [2, n-1]
if a^(n-1) % n not equal 1:
return composite
else
// for all q, prime factors of (n-1)
if a^(n-1)/q % n not equal 1
return prime
Return probably prime
Problems Associated with Lucas’s test are :
- Knowing all of the prime factors of n-1
- Finding an appropriate choice for a
C++
#include <bits/stdc++.h>
using namespace std;
void primeFactors(int n, vector<int>& factors)
{
if (n % 2 == 0)
factors.push_back(2);
while (n % 2 == 0)
n = n / 2;
for (int i = 3; i <= sqrt(n); i += 2) {
if (n % i == 0)
factors.push_back(i);
while (n % i == 0)
n = n / i;
}
if (n > 2)
factors.push_back(n);
}
int power(int n, int r, int q)
{
int total = n;
for (int i = 1; i < r; i++)
total = (total * n) % q;
return total;
}
string lucasTest(int n)
{
if (n == 1)
return "neither prime nor composite";
if (n == 2)
return "prime";
if (n % 2 == 0)
return "composite1";
vector<int> factors;
primeFactors(n - 1, factors);
int random[n - 3];
for (int i = 0; i < n - 2; i++)
random[i] = i + 2;
shuffle(random, random + n - 3,
default_random_engine(time(0)));
for (int i = 0; i < n - 2; i++) {
int a = random[i];
if (power(a, n - 1, n) != 1)
return "composite";
bool flag = true;
for (int k = 0; k < factors.size(); k++) {
if (power(a, (n - 1) / factors[k], n) == 1) {
flag = false;
break;
}
}
if (flag)
return "prime";
}
return "probably composite";
}
int main()
{
cout << 7 << " is " << lucasTest(7) << endl;
cout << 9 << " is " << lucasTest(9) << endl;
cout << 37 << " is " << lucasTest(37) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG {
static ArrayList<Integer> factors
= new ArrayList<Integer>();
static ArrayList<Integer> primeFactors(int n)
{
if (n % 2 == 0)
factors.add(2);
while (n % 2 == 0)
n = n / 2;
for (int i = 3; i <= Math.sqrt(n); i += 2) {
if (n % i == 0)
factors.add(i);
while (n % i == 0)
n = n / i;
}
if (n > 2)
factors.add(n);
return factors;
}
static int power(int n, int r, int q)
{
int total = n;
for (int i = 1; i < r; i++)
total = (total * n) % q;
return total;
}
static String lucasTest(int n)
{
if (n == 1)
return "neither prime nor composite";
if (n == 2)
return "prime";
if (n % 2 == 0)
return "composite1";
primeFactors(n - 1);
int[] random = new int[n - 2];
for (int i = 0; i < n - 2; i++)
random[i] = i + 2;
Collections.shuffle(Arrays.asList(random));
for (int i = 0; i < n - 2; i++) {
int a = random[i];
if (power(a, n - 1, n) != 1)
return "composite";
boolean flag = true;
for (i = 0; i < factors.size(); i++) {
if (power(a, (n - 1) / factors.get(i), n) == 1) {
flag = false;
break;
}
}
if (flag)
return "prime";
}
return "probably composite";
}
public static void main(String[] args)
{
System.out.println(7 + " is " + lucasTest(7));
System.out.println(9 + " is " + lucasTest(9));
System.out.println(37 + " is " + lucasTest(37));
}
}
|
Python3
import random
import math
def primeFactors(n, factors):
if (n % 2 == 0):
factors.append(2)
while (n % 2 == 0):
n = n // 2
for i in range(3, int(math.sqrt(n)) + 1, 2):
if (n % i == 0):
factors.append(i)
while (n % i == 0):
n = n // i
if (n > 2):
factors.append(n)
return factors
def power(n, r, q):
total = n
for i in range(1, r):
total = (total * n) % q
return total
def lucasTest(n):
if (n == 1):
return "neither prime nor composite"
if (n == 2):
return "prime"
if (n % 2 == 0):
return "composite1"
factors = []
factors = primeFactors(n - 1, factors)
rand = [i + 2 for i in range(n - 3)]
random.shuffle(rand)
for i in range(n - 2):
a = rand[i]
if (power(a, n - 1, n) != 1):
return "composite"
flag = True
for k in range(len(factors)):
if (power(a, (n - 1) // factors[k], n) == 1):
flag = False
break
if (flag):
return "prime"
return "probably composite"
if __name__=="__main__":
print(str(7) + " is " + lucasTest(7))
print(str(9) + " is " + lucasTest(9))
print(str(37) + " is " + lucasTest(37))
|
C#
using System;
using System.Linq;
using System.Collections.Generic;
class GFG
{
static List<int> factors = new List<int>();
static List<int> primeFactors(int n)
{
if (n % 2 == 0)
factors.Add(2);
while (n % 2 == 0)
n = n / 2;
for (int i = 3; i <= Math.Sqrt(n); i += 2) {
if (n % i == 0)
factors.Add(i);
while (n % i == 0)
n = n / i;
}
if (n > 2)
factors.Add(n);
return factors;
}
static int power(int n, int r, int q)
{
int total = n;
for (int i = 1; i < r; i++)
total = (total * n) % q;
return total;
}
static string lucasTest(int n)
{
if (n == 1)
return "neither prime nor composite";
if (n == 2)
return "prime";
if (n % 2 == 0)
return "composite1";
primeFactors(n - 1);
int[] random = new int[n - 2];
for (int i = 0; i < n - 2; i++)
random[i] = i + 2;
Random rand = new Random();
random = random.OrderBy(x => rand.Next()).ToArray();
for (int i = 0; i < n - 2; i++) {
int a = random[i];
if (power(a, n - 1, n) != 1)
return "composite";
bool flag = true;
foreach (var factor in factors) {
if (power(a, (n - 1) / factor, n) == 1) {
flag = false;
break;
}
}
if (flag)
return "prime";
}
return "probably composite";
}
public static void Main(string[] args)
{
Console.WriteLine(7 + " is " + lucasTest(7));
Console.WriteLine(9 + " is " + lucasTest(9));
Console.WriteLine(37 + " is " + lucasTest(37));
}
}
|
Javascript
function shuffle(arr){
for(let i = arr.length-1; i>0;i--){
let j = Math.floor(Math.random() * (i+1));
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
return arr;
}
function primeFactors(n, factors) {
if (n % 2 == 0){
factors.push(2);
}
while (n % 2 == 0){
n = n / 2;
}
for (let i = 3; i <= Math.sqrt(n); i += 2) {
if (n % i == 0){
factors.push(i);
}
while (n % i == 0){
n = n / i;
}
}
if (n > 2){
factors.push(n);
}
}
function power(n, r, q) {
let total = n;
for (let i = 1; i < r; i++){
total = (total * n) % q;
}
return total;
}
function lucasTest(n) {
if (n == 1){
return "neither prime nor composite";
}
if (n == 2){
return "prime";
}
if (n % 2 == 0){
return "composite1";
}
const factors = [];
primeFactors(n - 1, factors);
const random = [];
for (let i = 0; i < n - 2; i++){
random.push(i+2);
}
shuffle(random);
for (let i = 0; i < n - 2; i++) {
let a = random[i];
if (power(a, n - 1, n) != 1){
return "composite";
}
let flag = true;
for (let k = 0; k < factors.length; k++) {
if (power(a, (n - 1) / factors[k], n) == 1) {
flag = false;
break;
}
}
if (flag){
return "prime";
}
}
return "probably composite";
}
{
console.log( 7 + " is " + lucasTest(7));
console.log( 9 + " is " + lucasTest(9));
console.log( 37 + " is " + lucasTest(37));
return 0;
}
Javascript
|
Output:
7 is prime
9 is composite
37 is prime
Time Complexity: O(nlogn)
Auxiliary Space: O(n)
This method is quite complicated and inefficient as compared to other primality tests. And the main problems are factors of ‘n-1’ and choosing appropriate ‘a’.
Other Primality tests:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...