Breadth First Search or BFS for a Graph
Last Updated :
09 Aug, 2024
Breadth First Search (BFS) is a fundamental graph traversal algorithm. It begins with a node, then first traverses all its adjacent. Once all adjacent are visited, then their adjacent are traversed. This is different from DFS in a way that closest vertices are visited before others. We mainly traverse vertices level by level. A lot of popular graph algorithms like Dijkstra’s shortest path, Kahn’s Algorithm, and Prim’s algorithm are based on BFS. BFS itself can be used to detect cycle in a directed and undirected graph, find shortest path in an unweghted graph and many more problems.
BFS from a Given Source:
The algorithm starts from a given source and explores all reachable vertices from the given source. It is similar to the Breadth-First Traversal of a tree. Like tree, we begin with the given source (in tree, we begin with root) and traverse vertices level by level using a queue data structure. The only catch here is that, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array.
Initialization: Enqueue the given source vertex into a queue and mark it as visited.
- Exploration: While the queue is not empty:
- Dequeue a node from the queue and visit it (e.g., print its value).
- For each unvisited neighbor of the dequeued node:
- Enqueue the neighbor into the queue.
- Mark the neighbor as visited.
- Termination: Repeat step 2 until the queue is empty.
This algorithm ensures that all nodes in the graph are visited in a breadth-first manner, starting from the starting node.
How Does the BFS Algorithm Work?
Let us understand the working of the algorithm with the help of the following example where the source vertex is 0.
Step1: Initially queue and visited arrays are empty.
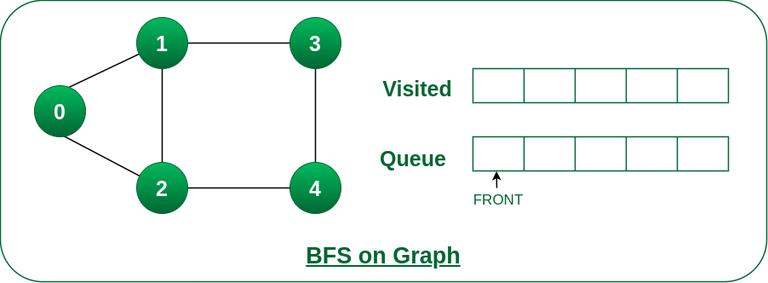
Queue and visited arrays are empty initially.
Step2: Push 0 into queue and mark it visited.
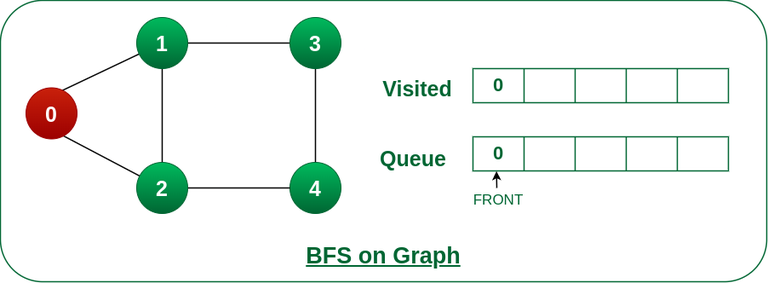
Push node 0 into queue and mark it visited.
Step 3: Remove 0 from the front of queue and visit the unvisited neighbours and push them into queue.
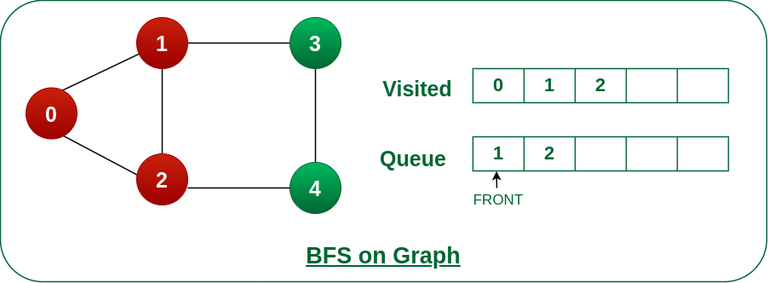
Remove node 0 from the front of queue and visited the unvisited neighbours and push into queue.
Step 4: Remove node 1 from the front of queue and visit the unvisited neighbours and push them into queue.
Remove node 1 from the front of queue and visited the unvisited neighbours and push
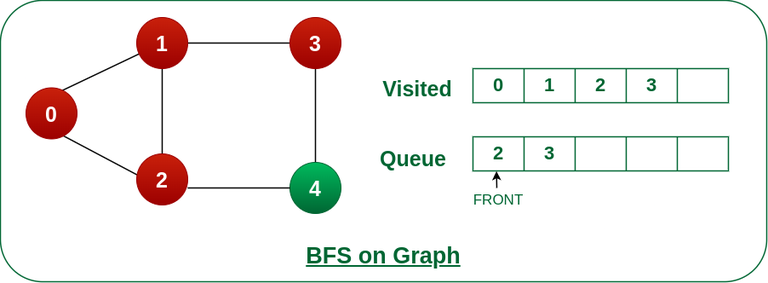
Step 5: Remove node 2 from the front of queue and visit the unvisited neighbours and push them into queue.
Remove node 2 from the front of queue and visit the unvisited neighbours and push them into queue.
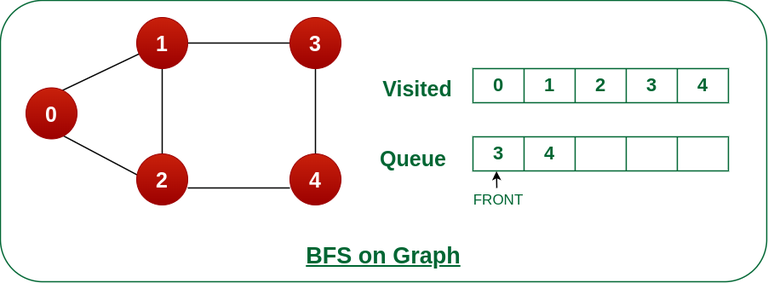
Step 6: Remove node 3 from the front of queue and visit the unvisited neighbours and push them into queue.
As we can see that every neighbours of node 3 is visited, so move to the next node that are in the front of the queue.
Remove node 3 from the front of queue and visit the unvisited neighbours and push them into queue.
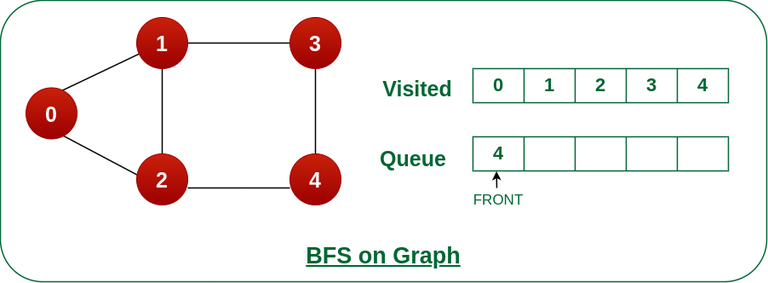
Steps 7: Remove node 4 from the front of queue and visit the unvisited neighbours and push them into queue.
As we can see that every neighbours of node 4 are visited, so move to the next node that is in the front of the queue.
Remove node 4 from the front of queue and visit the unvisited neighbours and push them into queue.
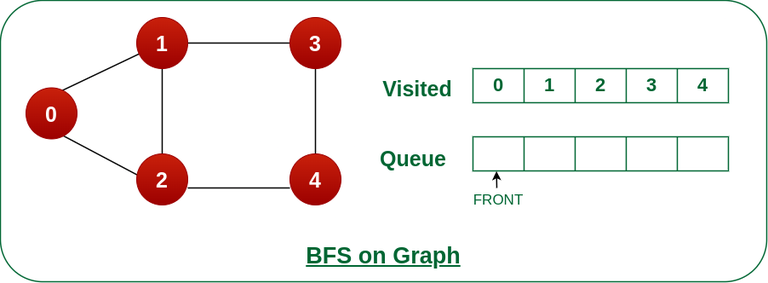
Now, Queue becomes empty, So, terminate these process of iteration.
To deepen your understanding of BFS and other essential algorithms, consider enrolling in our comprehensive course, Tech Interview 101 – From DSA to System Design . This course covers data structures and algorithms from basic to advanced levels , providing you with the skills needed to excel in technical exams and interviews. Building a strong foundation in these concepts is crucial for your success in the tech industry.
// C++ program for BFS of an undirected graph
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// BFS from given source s
void bfs(vector<vector<int>>& adj, int s,
vector<bool>& visited)
{
// Create a queue for BFS
queue<int> q;
// Mark the source node as visited and
// enqueue it
visited[s] = true;
q.push(s);
// Iterate over the queue
while (!q.empty()) {
// Dequeue a vertex from queue and print it
int curr = q.front();
q.pop();
cout << curr << " ";
// Get all adjacent vertices of the dequeued
// vertex curr If an adjacent has not been
// visited, mark it visited and enqueue it
for (int x : adj[curr]) {
if (!visited[x]) {
visited[x] = true;
q.push(x);
}
}
}
}
// Function to add an edge to the graph
void addEdge(vector<vector<int>>& adj,
int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u); // Undirected Graph
}
int main()
{
// Number of vertices in the graph
int V = 5;
// Adjacency list representation of the graph
vector<vector<int>> adj(V);
// Add edges to the graph
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 4);
// Mark all the vertices as not visited
vector<bool> visited(V, false);
// Perform BFS traversal starting from vertex 0
cout << "BFS starting from 0 : \n";
bfs(adj, 0, visited);
return 0;
}
// C program for BFS of an undirected graph
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 100
// Structure to represent a node in adjacency list
struct Node {
int data;
struct Node* next;
};
// Function to create a new node
struct Node* createNode(int data) {
struct Node* newNode =
(struct Node*)malloc(sizeof(struct Node));
newNode->data = data;
newNode->next = NULL;
return newNode;
}
// Function to add an edge to the graph
void addEdge(struct Node* adj[], int u, int v) {
struct Node* newNode = createNode(v);
newNode->next = adj[u];
adj[u] = newNode;
// Undirected graph
newNode = createNode(u);
newNode->next = adj[v];
adj[v] = newNode;
}
// Function to perform Breadth First Search on a graph
// represented using adjacency list
void bfs(struct Node* adj[], int vertices,
int source, int visited[]) {
// Create a queue for BFS
int queue[MAX_VERTICES];
int front = 0, rear = 0;
// Mark the current node as visited and enqueue it
visited[source] = 1;
queue[rear++] = source;
// Iterate over the queue
while (front != rear) {
// Dequeue a vertex from queue and print it
int curr = queue[front++];
printf("%d ", curr);
// Get all adjacent vertices of the dequeued vertex
// curr If an adjacent has not been visited,
// then mark it visited and enqueue it
struct Node* temp = adj[curr];
while (temp != NULL) {
int neighbor = temp->data;
if (!visited[neighbor]) {
visited[neighbor] = 1;
queue[rear++] = neighbor;
}
temp = temp->next;
}
}
}
int main() {
// Number of vertices in the graph
int vertices = 5;
// Adjacency list representation of the graph
struct Node* adj[vertices];
for (int i = 0; i < vertices; ++i)
adj[i] = NULL;
// Add edges to the graph
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 4);
// Mark all the vertices as not visited
int visited[vertices];
for (int i = 0; i < vertices; ++i)
visited[i] = 0;
// Perform BFS traversal starting from vertex 0
printf("Breadth First Traversal "
"starting from vertex 0: ");
bfs(adj, vertices, 0, visited);
return 0;
}
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class GfG {
// BFS from given source s
static void bfs(List<List<Integer>> adj, int s,
boolean[] visited) {
// Create a queue for BFS
Queue<Integer> q = new LinkedList<>();
// Mark the source node as visited and
// enqueue it
visited[s] = true;
q.offer(s);
// Iterate over the queue
while (!q.isEmpty()) {
// Dequeue a vertex from queue and print it
int curr = q.poll();
System.out.print(curr + " ");
// Get all adjacent vertices of the dequeued
// vertex. If an adjacent has not been visited,
// mark it visited and enqueue it
for (int x : adj.get(curr)) {
if (!visited[x]) {
visited[x] = true;
q.offer(x);
}
}
}
}
// Function to add an edge to the graph
static void addEdge(List<List<Integer>> adj,
int u, int v) {
adj.get(u).add(v);
adj.get(v).add(u);
}
public static void main(String[] args) {
// Number of vertices in the graph
int V = 5;
// Adjacency list representation of the graph
List<List<Integer>> adj = new ArrayList<>();
for (int i = 0; i < V; i++) {
adj.add(new ArrayList<>());
}
// Add edges to the graph
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 4);
// Mark all the vertices as not visited
boolean[] visited = new boolean[V];
// Perform BFS traversal starting from vertex 0
System.out.println("BFS starting from 0 : ");
bfs(adj, 0, visited);
}
}
from collections import deque
# BFS from given source s
def bfs(adj, s, visited):
# Create a queue for BFS
q = deque()
# Mark the source node as visited and enqueue it
visited[s] = True
q.append(s)
# Iterate over the queue
while q:
# Dequeue a vertex from queue and print it
curr = q.popleft()
print(curr, end=" ")
# Get all adjacent vertices of the dequeued
# vertex. If an adjacent has not been visited,
# mark it visited and enqueue it
for x in adj[curr]:
if not visited[x]:
visited[x] = True
q.append(x)
# Function to add an edge to the graph
def add_edge(adj, u, v):
adj[u].append(v)
adj[v].append(u)
# Example usage
if __name__ == "__main__":
# Number of vertices in the graph
V = 5
# Adjacency list representation of the graph
adj = [[] for _ in range(V)]
# Add edges to the graph
add_edge(adj, 0, 1)
add_edge(adj, 0, 2)
add_edge(adj, 1, 3)
add_edge(adj, 1, 4)
add_edge(adj, 2, 4)
# Mark all the vertices as not visited
visited = [False] * V
# Perform BFS traversal starting from vertex 0
print("BFS starting from 0: ")
bfs(adj, 0, visited)
using System;
using System.Collections.Generic;
class GfG {
// BFS from given source s
static void Bfs(List<List<int>> adj, int s,
bool[] visited) {
// Create a queue for BFS
Queue<int> q = new Queue<int>();
// Mark the source node as visited and enqueue it
visited[s] = true;
q.Enqueue(s);
// Iterate over the queue
while (q.Count > 0) {
// Dequeue a vertex from queue and print it
int curr = q.Dequeue();
Console.Write(curr + " ");
// Get all adjacent vertices of the dequeued vertex
// If an adjacent has not been visited,
// mark it visited and enqueue it
foreach (int x in adj[curr]) {
if (!visited[x]) {
visited[x] = true;
q.Enqueue(x);
}
}
}
}
// Function to add an edge to the graph
static void AddEdge(List<List<int>> adj,
int u, int v) {
adj[u].Add(v);
adj[v].Add(u);
}
public static void Main(string[] args) {
// Number of vertices in the graph
int V = 5;
// Adjacency list representation of the graph
List<List<int>> adj = new List<List<int>>(V);
for (int i = 0; i < V; i++) {
adj.Add(new List<int>());
}
// Add edges to the graph
AddEdge(adj, 0, 1);
AddEdge(adj, 0, 2);
AddEdge(adj, 1, 3);
AddEdge(adj, 1, 4);
AddEdge(adj, 2, 4);
// Mark all the vertices as not visited
bool[] visited = new bool[V];
// Perform BFS traversal starting from vertex 0
Console.WriteLine("BFS starting from 0 : ");
Bfs(adj, 0, visited);
}
}
// BFS from given source s
function bfs(s) {
const visited = Array(V).fill(false);
const queue = [];
// Mark the source node as visited
// and enqueue it
visited[s] = true;
queue.push(s);
// Iterate over the queue
while (queue.length) {
// Dequeue a vertex from queue and print it
const curr = queue.shift();
process.stdout.write(curr + " ");
// Get all adjacent vertices of the dequeued
// vertex. If an adjacent has not been visited,
// mark it visited and enqueue it
for (const x of adj[curr]) {
if (!visited[x]) {
visited[x] = true;
queue.push(x);
}
}
}
}
// Function to add an edge to the graph
function addEdge(u, v) {
adj[u].push(v);
adj[v].push(u);
}
// Example usage
const V = 5;
const adj = Array.from({ length: V }, () => []);
addEdge(0, 1);
addEdge(0, 2);
addEdge(1, 3);
addEdge(1, 4);
addEdge(2, 4);
console.log("BFS starting from 0:");
bfs(0);
OutputBreadth First Traversal starting from vertex 0: 0 1 2 3 4
Time Complexity: O(V+E), where V is the number of nodes and E is the number of edges.
Auxiliary Space: O(V)
BFS of the whole Graph which Maybe Disconnected
The above implementation takes a source as an input and prints only those vertices that are reachable from the source and would not print all vertices in case of disconnected graph. Let us now talk about the algorithm that prints all vertices without any source and the graph maybe disconnected.
The idea is simple, instead of calling BFS for a single vertex, we call the above implemented BFS for all all non-visited vertices one by one.
C++
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// BFS from given source s
void bfs(vector<vector<int>>& adj, int s,
vector<bool>& visited)
{
queue<int> q; // Create a queue for BFS
// Mark the source node as visited and enqueue it
visited[s] = true;
q.push(s);
// Iterate over the queue
while (!q.empty()) {
int curr = q.front(); // Dequeue a vertex
q.pop();
cout << curr << " ";
// Get all adjacent vertices of curr
for (int x : adj[curr]) {
if (!visited[x]) {
visited[x] = true; // Mark as visited
q.push(x); // Enqueue it
}
}
}
}
// Function to add an edge to the graph
void addEdge(vector<vector<int>>& adj, int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
// Perform BFS for the entire graph
void bfsDisconnected(vector<vector<int>>& adj) {
vector<bool> visited(adj.size(), false); // Not visited
for (int i = 0; i < adj.size(); ++i) {
if (!visited[i]) {
bfs(adj, i, visited);
}
}
}
int main()
{
int V = 6; // Number of vertices
vector<vector<int>> adj(V); // Adjacency list
// Add edges to the graph
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 3, 4);
addEdge(adj, 4, 5);
// Perform BFS traversal for the entire graph
bfsDisconnected(adj);
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 100
// Structure to represent a node in adjacency list
struct Node {
int data;
struct Node* next;
};
// Function to create a new node
struct Node* createNode(int data)
{
struct Node* newNode =
(struct Node*)malloc(sizeof(struct Node));
newNode->data = data;
newNode->next = NULL;
return newNode;
}
// Function to add an edge to the graph
void addEdge(struct Node* adj[], int u, int v)
{
struct Node* newNode = createNode(v);
newNode->next = adj[u];
adj[u] = newNode;
// Undirected graph
newNode = createNode(v);
newNode->next = adj[u];
adj[u] = newNode;
}
// Function to perform BFS
void bfs(struct Node* adj[], int V, int s,
int visited[])
{
int queue[MAX_VERTICES];
int front = 0, rear = 0;
visited[s] = 1; // Mark source as visited
queue[rear++] = s; // Enqueue source
while (front != rear) {
int curr = queue[front++]; // Dequeue vertex
printf("%d ", curr);
// Get all adjacent vertices of curr
struct Node* temp = adj[curr];
while (temp != NULL) {
int neighbor = temp->data;
if (!visited[neighbor]) {
visited[neighbor] = 1; // Mark as visited
queue[rear++] = neighbor; // Enqueue it
}
temp = temp->next;
}
}
}
// Function to perform BFS for the entire graph
void bfsDisconnected(struct Node* adj[], int V)
{
int visited[V] = {0}; // Not visited
for (int i = 0; i < V; ++i) {
if (!visited[i]) {
bfs(adj, V, i, visited);
}
}
}
int main()
{
int V = 6; // Number of vertices
struct Node* adj[V];
for (int i = 0; i < V; ++i) {
adj[i] = NULL; // Initialize adjacency list
}
// Add edges to the graph
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 3, 4);
addEdge(adj, 4, 5);
// Perform BFS traversal for the entire graph
bfsDisconnected(adj, V);
return 0;
}
import java.util.*;
public class GfG {
// Function to add an edge to the graph
public static void addEdge(List<List<Integer>> adj,
int u, int v) {
adj.get(u).add(v);
adj.get(v).add(u); // Undirected graph
}
// BFS from given source s
public static void bfs(List<List<Integer>> adj,
int s, boolean[] visited) {
Queue<Integer> q = new LinkedList<>(); /
// Mark the source node as visited and enqueue it
visited[s] = true;
q.add(s);
// Iterate over the queue
while (!q.isEmpty()) {
int curr = q.poll(); // Dequeue a vertex
System.out.print(curr + " ");
// Get all adjacent vertices of curr
for (int x : adj.get(curr)) {
if (!visited[x]) {
visited[x] = true; // Mark as visited
q.add(x); // Enqueue it
}
}
}
}
// Perform BFS for the entire graph
public static void bfsDisconnected(List<List<Integer>> adj) {
boolean[] visited = new boolean[adj.size()]; // Not visited
for (int i = 0; i < adj.size(); i++) {
if (!visited[i]) {
bfs(adj, i, visited);
}
}
}
public static void main(String[] args) {
int V = 6; // Number of vertices
List<List<Integer>> adj = new ArrayList<>(V);
// Initialize adjacency lists
for (int i = 0; i < V; i++) {
adj.add(new ArrayList<>());
}
// Add edges to the graph
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 3, 4);
addEdge(adj, 4, 5);
// Perform BFS traversal for the entire graph
bfsDisconnected(adj);
}
}
from collections import deque
# BFS from given source s
def bfs(adj, s, visited):
q = deque() # Create a queue for BFS
# Mark the source node as visited and enqueue it
visited[s] = True
q.append(s)
# Iterate over the queue
while q:
curr = q.popleft() # Dequeue a vertex
print(curr, end=" ")
# Get all adjacent vertices of curr
for x in adj[curr]:
if not visited[x]:
visited[x] = True # Mark as visited
q.append(x) # Enqueue it
# Function to add an edge to the graph
def add_edge(adj, u, v):
adj[u].append(v)
adj[v].append(u) # Undirected graph
# Perform BFS for the entire graph
def bfs_disconnected(adj):
visited = [False] * len(adj) # Not visited
for i in range(len(adj)):
if not visited[i]:
bfs(adj, i, visited)
# Example usage
V = 6 # Number of vertices
adj = [[] for _ in range(V)] # Adjacency list
# Add edges to the graph
add_edge(adj, 0, 1)
add_edge(adj, 0, 2)
add_edge(adj, 3, 4)
add_edge(adj, 4, 5)
# Perform BFS traversal for the entire graph
bfs_disconnected(adj)
using System;
using System.Collections.Generic;
class Program
{
// Function to add an edge to the graph
static void AddEdge(List<List<int>> adj, int u, int v) {
adj[u].Add(v);
adj[v].Add(u); // Undirected graph
}
// BFS from given source s
static void Bfs(List<List<int>> adj, int s, bool[] visited) {
Queue<int> q = new Queue<int>(); // Create a queue for BFS
// Mark the source node as visited and enqueue it
visited[s] = true;
q.Enqueue(s);
// Iterate over the queue
while (q.Count > 0) {
int curr = q.Dequeue(); // Dequeue a vertex
Console.Write(curr + " ");
// Get all adjacent vertices of curr
foreach (int x in adj[curr]) {
if (!visited[x]) {
visited[x] = true; // Mark as visited
q.Enqueue(x); // Enqueue it
}
}
}
}
// Perform BFS for the entire graph
static void BfsDisconnected(List<List<int>> adj) {
bool[] visited = new bool[adj.Count]; // Not visited
for (int i = 0; i < adj.Count; i++) {
if (!visited[i]) {
Bfs(adj, i, visited);
}
}
}
static void Main() {
int V = 6; // Number of vertices
List<List<int>> adj = new List<List<int>>(V);
// Initialize adjacency lists
for (int i = 0; i < V; i++) {
adj.Add(new List<int>());
}
// Add edges to the graph
AddEdge(adj, 0, 1);
AddEdge(adj, 0, 2);
AddEdge(adj, 3, 4);
AddEdge(adj, 4, 5);
// Perform BFS traversal for the entire graph
BfsDisconnected(adj);
}
}
// Function to add an edge to the graph
function addEdge(adj, u, v) {
adj[u].push(v);
adj[v].push(u); // Undirected graph
}
// BFS from given source s
function bfs(adj, s, visited) {
let q = []; // Create a queue for BFS
// Mark the source node as visited and enqueue it
visited[s] = true;
q.push(s);
// Iterate over the queue
while (q.length > 0) {
let curr = q.shift(); // Dequeue a vertex
console.log(curr + " ");
// Get all adjacent vertices of curr
for (let x of adj[curr]) {
if (!visited[x]) {
visited[x] = true; // Mark as visited
q.push(x); // Enqueue it
}
}
}
}
// Perform BFS for the entire graph
function bfsDisconnected(adj) {
let visited = Array(adj.length).fill(false); // Not visited
for (let i = 0; i < adj.length; i++) {
if (!visited[i]) {
bfs(adj, i, visited);
}
}
}
// Example usage
let V = 6; // Number of vertices
let adj = Array.from({ length: V }, () => []);
// Add edges to the graph
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 3, 4);
addEdge(adj, 4, 5);
// Perform BFS traversal for the entire graph
bfsDisconnected(adj);
Complexity Analysis of Breadth-First Search (BFS) Algorithm:
Time Complexity of BFS Algorithm: O(V + E)
- BFS explores all the vertices and edges in the graph. In the worst case, it visits every vertex and edge once. Therefore, the time complexity of BFS is O(V + E), where V and E are the number of vertices and edges in the given graph.
Auxiliary Space of BFS Algorithm: O(V)
- BFS uses a queue to keep track of the vertices that need to be visited. In the worst case, the queue can contain all the vertices in the graph. Therefore, the space complexity of BFS is O(V).
Applications of BFS in Graphs:
BFS has various applications in graph theory and computer science, including:
- Shortest Path Finding: BFS can be used to find the shortest path between two nodes in an unweighted graph. By keeping track of the parent of each node during the traversal, the shortest path can be reconstructed.
- Cycle Detection: BFS can be used to detect cycles in a graph. If a node is visited twice during the traversal, it indicates the presence of a cycle.
- Connected Components: BFS can be used to identify connected components in a graph. Each connected component is a set of nodes that can be reached from each other.
- Topological Sorting: BFS can be used to perform topological sorting on a directed acyclic graph (DAG). Topological sorting arranges the nodes in a linear order such that for any edge (u, v), u appears before v in the order.
- Level Order Traversal of Binary Trees: BFS can be used to perform a level order traversal of a binary tree. This traversal visits all nodes at the same level before moving to the next level.
- Network Routing: BFS can be used to find the shortest path between two nodes in a network, making it useful for routing data packets in network protocols.
Problems on Breadth First Search or BFS for a Graph:
FAQs on Breadth First Search (BFS) for a Graph:
Question 1: What is BFS and how does it work?
Answer: BFS is a graph traversal algorithm that systematically explores a graph by visiting all the vertices at a given level before moving on to the next level. It starts from a starting vertex, enqueues it into a queue, and marks it as visited. Then, it dequeues a vertex from the queue, visits it, and enqueues all its unvisited neighbors into the queue. This process continues until the queue is empty.
Question 2: What are the applications of BFS?
Answer: BFS has various applications, including finding the shortest path in an unweighted graph, detecting cycles in a graph, topologically sorting a directed acyclic graph (DAG), finding connected components in a graph, and solving puzzles like mazes and Sudoku.
Question 3: What is the time complexity of BFS?
Answer: The time complexity of BFS is O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Question 4: What is the space complexity of BFS?
Answer: The space complexity of BFS is O(V), as it uses a queue to keep track of the vertices that need to be visited.
Question 5: What are the advantages of using BFS?
Answer: BFS is simple to implement and efficient for finding the shortest path in an unweighted graph. It also guarantees that all the vertices in the graph are visited.
Related Articles:
Please Login to comment...