Discrete logarithm (Find an integer k such that a^k is congruent modulo b)

Difficulty Level : Medium
Last Updated : 29 Dec, 2021

Given three integers a, b and m. Find an integer k such that 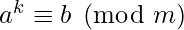$a^k \equiv b \pmod m$ where a and m are relatively prime. If it is not possible for any k to satisfy this relation, print -1.
Examples:

Input: 2 3 5
Output: 3
Explanation:
a = 2, b = 3, m = 5
The value which satisfies the above equation
is 3, because 
=> 2³ = 2 * 2 * 2 = 8
=> 2³ (mod 5) = 8 (mod 5) 
=> 3
which is equal to b i.e., 3.

Input: 3 7 11
Output: -1

A Naive approach is to run a loop from 0 to m to cover all possible values of k and check for which value of k, the above relation satisfies. If all the values of k exhausted, print -1. Time complexity of this approach is O(m)
An efficient approach is to use baby-step, giant-step algorithm by using meet in the middle trick.

Baby-step giant-step algorithm

Given a cyclic group G of order ‘m’, a generator ‘a’ of the group, and a group element ‘b’, the problem is to find an integer ‘k’ such that 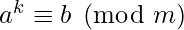$a^k \equiv b \pmod m$
So what we are going to do(according to Meet in the middle trick) is to split the problem in two parts of $\text{[math]}$ each and solve them individually and then find the collision.

Now according to the baby-step giant-step 
algorithm, we can write 'k' as 
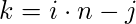 with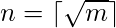  
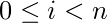and  and .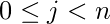
Therefore, we have:


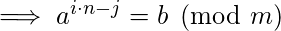
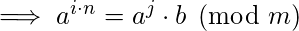Therefore in order to solve, we precompute 
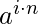 for different values of 'i'. 
Then fix 'b' and tries values of 'j' 
In RHS of the congruence relation above. It 
tests to see if congruence is satisfied for 
any value of 'j', using precomputed 
values of LHS.

Let’s see how to use above algorithm for our question:-
First of all we have to write 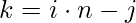$k = i\cdot n - j$ , where 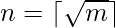$n = \left\lceil \sqrt{m} \right\rceil$ Obviously, any value of k in the interval [0, m) can be represented in this form, where 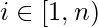$i \in [1, n)$ and $j \in [0, n)$
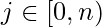
Replace the ‘k’ in above equality, we get:-
$\implies a^k = b \pmod m$
$\implies a^{i\cdot n - j} = b \pmod m$
$\implies a^{i\cdot n} = a^j\cdot b \pmod m$

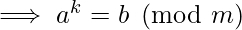
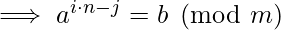
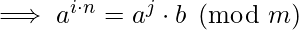
The term left and right can take only n distinct values as 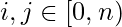$i, j \in [0, n)$ . Therefore we need to generate all these terms for either left or right part of equality and store them in an array or data structure like map/unordered_map in C/C++ or Hashmap in java.
Suppose we have stored all values of LHS. Now iterate over all possible terms on the RHS for different values of j and check which value satisfies the LHS equality.
If no value satisfies in above step for any candidate of j, print -1.

C++

// C++ program to calculate discrete logarithm
#include<bits/stdc++.h>
using namespace std;
 
/* Iterative Function to calculate (x ^ y)%p in
   O(log y) */
int powmod(int x, int y, int p)
{
    int res = 1;  // Initialize result
 
    x = x % p;  // Update x if it is more than or
                // equal to p
 
    while (y > 0)
    {
        // If y is odd, multiply x with result
        if (y & 1)
            res = (res*x) % p;
 
        // y must be even now
        y = y>>1; // y = y/2
        x = (x*x) % p;
    }
    return res;
}
 
// Function to calculate k for given a, b, m
int discreteLogarithm(int a, int b, int m) {
 
    int n = (int) sqrt (m) + 1;
 
    unordered_map<int, int> value;
 
    // Store all values of a^(n*i) of LHS
    for (int i = n; i >= 1; --i)
        value[ powmod (a, i * n, m) ] = i;
 
    for (int j = 0; j < n; ++j)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        int cur = (powmod (a, j, m) * b) % m;
 
        // If collision occurs i.e., LHS = RHS
        if (value[cur])
        {
            int ans = value[cur] * n - j;
            // Check whether ans lies below m or not
            if (ans < m)
                return ans;
        }
    }
    return -1;
}
 
// Driver code
int main()
{
    int a = 2, b = 3, m = 5;
    cout << discreteLogarithm(a, b, m) << endl;
 
    a = 3, b = 7, m = 11;
    cout << discreteLogarithm(a, b, m);
}

Java

// Java program to calculate discrete logarithm
 
class GFG{
/* Iterative Function to calculate (x ^ y)%p in
O(log y) */
static int powmod(int x, int y, int p)
{
    int res = 1; // Initialize result
 
    x = x % p; // Update x if it is more than or
                // equal to p
 
    while (y > 0)
    {
        // If y is odd, multiply x with result
        if ((y & 1)>0)
            res = (res*x) % p;
 
        // y must be even now
        y = y>>1; // y = y/2
        x = (x*x) % p;
    }
    return res;
}
 
// Function to calculate k for given a, b, m
static int discreteLogarithm(int a, int b, int m) {
 
    int n = (int) (Math.sqrt (m) + 1);
 
    int[] value=new int[m];
 
    // Store all values of a^(n*i) of LHS
    for (int i = n; i >= 1; --i)
        value[ powmod (a, i * n, m) ] = i;
 
    for (int j = 0; j < n; ++j)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        int cur = (powmod (a, j, m) * b) % m;
 
        // If collision occurs i.e., LHS = RHS
        if (value[cur]>0)
        {
            int ans = value[cur] * n - j;
            // Check whether ans lies below m or not
            if (ans < m)
                return ans;
        }
    }
    return -1;
}
 
// Driver code
public static void main(String[] args)
{
    int a = 2, b = 3, m = 5;
    System.out.println(discreteLogarithm(a, b, m));
 
    a = 3;
    b = 7;
    m = 11;
    System.out.println(discreteLogarithm(a, b, m));
}
}
// This code is contributed by mits

Python3

# Python3 program to calculate
# discrete logarithm
import math;
 
# Iterative Function to calculate
# (x ^ y)%p in O(log y)
def powmod(x, y, p):
 
    res = 1; # Initialize result
 
    x = x % p; # Update x if it is more
               # than or equal to p
 
    while (y > 0):
         
        # If y is odd, multiply x with result
        if (y & 1):
            res = (res * x) % p;
 
        # y must be even now
        y = y >> 1; # y = y/2
        x = (x * x) % p;
    return res;
 
# Function to calculate k for given a, b, m
def discreteLogarithm(a, b, m):
    n = int(math.sqrt(m) + 1);
 
    value = [0] * m;
 
    # Store all values of a^(n*i) of LHS
    for i in range(n, 0, -1):
        value[ powmod (a, i * n, m) ] = i;
 
    for j in range(n):
         
        # Calculate (a ^ j) * b and check
        # for collision
        cur = (powmod (a, j, m) * b) % m;
 
        # If collision occurs i.e., LHS = RHS
        if (value[cur]):
            ans = value[cur] * n - j;
             
            # Check whether ans lies below m or not
            if (ans < m):
                return ans;
     
    return -1;
 
# Driver code
a = 2;
b = 3;
m = 5;
print(discreteLogarithm(a, b, m));
 
a = 3;
b = 7;
m = 11;
print(discreteLogarithm(a, b, m));
 
# This code is contributed by mits

C#

// C# program to calculate discrete logarithm
using System;
class GFG{
/* Iterative Function to calculate (x ^ y)%p in
O(log y) */
static int powmod(int x, int y, int p)
{
    int res = 1; // Initialize result
 
    x = x % p; // Update x if it is more than or
                // equal to p
 
    while (y > 0)
    {
        // If y is odd, multiply x with result
        if ((y & 1)>0)
            res = (res*x) % p;
 
        // y must be even now
        y = y>>1; // y = y/2
        x = (x*x) % p;
    }
    return res;
}
 
// Function to calculate k for given a, b, m
static int discreteLogarithm(int a, int b, int m) {
 
    int n = (int) (Math.Sqrt (m) + 1);
 
    int[] value=new int[m];
 
    // Store all values of a^(n*i) of LHS
    for (int i = n; i >= 1; --i)
        value[ powmod (a, i * n, m) ] = i;
 
    for (int j = 0; j < n; ++j)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        int cur = (powmod (a, j, m) * b) % m;
 
        // If collision occurs i.e., LHS = RHS
        if (value[cur]>0)
        {
            int ans = value[cur] * n - j;
            // Check whether ans lies below m or not
            if (ans < m)
                return ans;
        }
    }
    return -1;
}
 
// Driver code
static void Main()
{
    int a = 2, b = 3, m = 5;
    Console.WriteLine(discreteLogarithm(a, b, m));
 
    a = 3;
    b = 7;
    m = 11;
    Console.WriteLine(discreteLogarithm(a, b, m));
}
}
// This code is contributed by mits

PHP

<?php
// PHP program to calculate
// discrete logarithm
 
// Iterative Function to calculate
// (x ^ y)%p in O(log y)
function powmod($x, $y, $p)
{
    $res = 1; // Initialize result
 
    $x = $x % $p; // Update x if it is more
                  // than or equal to p
 
    while ($y > 0)
    {
        // If y is odd, multiply x with result
        if ($y & 1)
            $res = ($res * $x) % $p;
 
        // y must be even now
        $y = $y >> 1; // y = y/2
        $x = ($x * $x) % $p;
    }
    return $res;
}
 
// Function to calculate k for given a, b, m
function discreteLogarithm($a, $b, $m)
{
    $n = (int)sqrt($m) + 1;
 
    $value = array_fill(0, $m, NULL);
 
    // Store all values of a^(n*i) of LHS
    for ($i = $n; $i >= 1; --$i)
        $value[ powmod ($a, $i * $n, $m) ] = $i;
 
    for ($j = 0; $j < $n; ++$j)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        $cur = (powmod ($a, $j, $m) * $b) % $m;
 
        // If collision occurs i.e., LHS = RHS
        if ($value[$cur])
        {
            $ans = $value[$cur] * $n - $j;
             
            // Check whether ans lies below m or not
            if ($ans < $m)
                return $ans;
        }
    }
    return -1;
}
 
// Driver code
$a = 2;
$b = 3;
$m = 5;
echo discreteLogarithm($a, $b, $m), "\n";
 
$a = 3;
$b = 7;
$m = 11;
echo discreteLogarithm($a, $b, $m), "\n";
 
// This code is contributed by ajit.
?>

Javascript

<script>
 
    // Javascript program to calculate
    // discrete logarithm
     
    /* Iterative Function to
    calculate (x ^ y)%p in
    O(log y) */
    function powmod(x, y, p)
    {
        // Initialize result
        let res = 1;
 
        // Update x if it is more
        // than or
        // equal to p
        x = x % p;
                     
        while (y > 0)
        {
            // If y is odd, multiply x
            // with result
            if ((y & 1)>0)
                res = (res*x) % p;
 
            // y must be even now
            y = y>>1; // y = y/2
            x = (x*x) % p;
        }
        return res;
    }
 
    // Function to calculate
    // k for given a, b, m
    function discreteLogarithm(a, b, m) {
 
        let n = (parseInt(Math.sqrt(m), 10) + 1);
 
        let value = new Array(m);
        value.fill(0);
 
        // Store all values of a^(n*i) of LHS
        for (let i = n; i >= 1; --i)
            value[ powmod (a, i * n, m) ] = i;
 
        for (let j = 0; j < n; ++j)
        {
            // Calculate (a ^ j) * b and check
            // for collision
            let cur = (powmod (a, j, m) * b) % m;
 
            // If collision occurs
            // i.e., LHS = RHS
            if (value[cur]>0)
            {
                let ans = value[cur] * n - j;
                // Check whether ans lies
                // below m or not
                if (ans < m)
                    return ans;
            }
        }
        return -1;
    }
     
    let a = 2, b = 3, m = 5;
    document.write(
    discreteLogarithm(a, b, m) + "</br>"
    );
  
    a = 3;
    b = 7;
    m = 11;
    document.write(
    discreteLogarithm(a, b, m) + "</br>"
    );
 
</script>

Output:

3
-1

Time complexity: O(sqrt(m)*log(b))
Auxiliary space: O(sqrt(m))
A possible improvement is to get rid of binary exponentiation or log(b) factor in the second phase of the algorithm. This can be done by keeping a variable that multiplies by ‘a’ each time as ‘an’. Let’s see the program to understand more.

C++

// C++ program to calculate discrete logarithm
#include<bits/stdc++.h>
using namespace std;
 
int discreteLogarithm(int a, int b, int m)
{
    int n = (int) sqrt (m) + 1;
 
    // Calculate a ^ n
    int an = 1;
    for (int i = 0; i<n; ++i)
        an = (an * a) % m;
 
    unordered_map<int, int> value;
 
    // Store all values of a^(n*i) of LHS
    for (int i = 1, cur = an; i<= n; ++i)
    {
        if (! value[ cur ])
            value[ cur ] = i;
        cur = (cur * an) % m;
    }
 
    for (int i = 0, cur = b; i<= n; ++i)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        if (value[cur])
        {
            int ans = value[cur] * n - i;
            if (ans < m)
                return ans;
        }
        cur = (cur * a) % m;
    }
    return -1;
}
 
// Driver code
int main()
{
    int a = 2, b = 3, m = 5;
    cout << discreteLogarithm(a, b, m) << endl;
 
    a = 3, b = 7, m = 11;
    cout << discreteLogarithm(a, b, m);
}

Java

// Java program to calculate discrete logarithm
 
class GFG
{
 
    static int discreteLogarithm(int a, int b, int m)
    {
        int n = (int) (Math.sqrt (m) + 1);
 
        // Calculate a ^ n
        int an = 1;
        for (int i = 0; i < n; ++i)
            an = (an * a) % m;
 
        int[] value=new int[m];
 
        // Store all values of a^(n*i) of LHS
        for (int i = 1, cur = an; i <= n; ++i)
        {
            if (value[ cur ] == 0)
                value[ cur ] = i;
            cur = (cur * an) % m;
        }
 
        for (int i = 0, cur = b; i <= n; ++i)
        {
            // Calculate (a ^ j) * b and check
            // for collision
            if (value[cur] > 0)
            {
                int ans = value[cur] * n - i;
                if (ans < m)
                    return ans;
            }
            cur = (cur * a) % m;
        }
        return -1;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int a = 2, b = 3, m = 5;
        System.out.println(discreteLogarithm(a, b, m));
        a = 3;
        b = 7;
        m = 11;
        System.out.println(discreteLogarithm(a, b, m));
    }
}
 
// This code is contributed by mits

Python3

# Python3 program to calculate
# discrete logarithm
import math;
 
def discreteLogarithm(a, b, m):
 
    n = int(math.sqrt (m) + 1);
 
    # Calculate a ^ n
    an = 1;
    for i in range(n):
        an = (an * a) % m;
 
    value = [0] * m;
 
    # Store all values of a^(n*i) of LHS
    cur = an;
    for i in range(1, n + 1):
        if (value[ cur ] == 0):
            value[ cur ] = i;
        cur = (cur * an) % m;
     
    cur = b;
    for i in range(n + 1):
         
        # Calculate (a ^ j) * b and check
        # for collision
        if (value[cur] > 0):
            ans = value[cur] * n - i;
            if (ans < m):
                return ans;
        cur = (cur * a) % m;
 
    return -1;
 
# Driver code
a = 2;
b = 3;
m = 5;
print(discreteLogarithm(a, b, m));
 
a = 3;
b = 7;
m = 11;
print(discreteLogarithm(a, b, m));
 
# This code is contributed by mits

C#

// C# program to calculate discrete logarithm
using System;
 
class GFG
{
     
static int discreteLogarithm(int a, int b, int m)
{
    int n = (int) (Math.Sqrt (m) + 1);
 
    // Calculate a ^ n
    int an = 1;
    for (int i = 0; i < n; ++i)
        an = (an * a) % m;
 
    int[] value = new int[m];
 
    // Store all values of a^(n*i) of LHS
    for (int i = 1, cur = an; i<= n; ++i)
    {
        if (value[ cur ] == 0)
            value[ cur ] = i;
        cur = (cur * an) % m;
    }
 
    for (int i = 0, cur = b; i<= n; ++i)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        if (value[cur] > 0)
        {
            int ans = value[cur] * n - i;
            if (ans < m)
                return ans;
        }
        cur = (cur * a) % m;
    }
    return -1;
}
 
// Driver code
static void Main()
{
    int a = 2, b = 3, m = 5;
    Console.WriteLine(discreteLogarithm(a, b, m));
 
    a = 3;
    b = 7;
    m = 11;
    Console.WriteLine(discreteLogarithm(a, b, m));
}
}
 
// This code is contributed by mits

PHP

<?php
// PHP program to calculate discrete logarithm
 
function discreteLogarithm($a, $b, $m)
{
    $n = (int)sqrt ($m) + 1;
 
    // Calculate a ^ n
    $an = 1;
    for ($i = 0; $i < $n; ++$i)
        $an = ($an * $a) % $m;
 
    $value = array_fill(0, $m, NULL);
 
    // Store all values of a^(n*i) of LHS
    for ($i = 1, $cur = $an; $i<= $n; ++$i)
    {
        if (! $value[ $cur ])
            $value[ $cur ] = $i;
        $cur = ($cur * $an) % $m;
    }
 
    for ($i = 0, $cur = $b; $i<= $n; ++$i)
    {
        // Calculate (a ^ j) * b and check
        // for collision
        if ($value[$cur])
        {
            $ans = $value[$cur] * $n - $i;
            if ($ans < $m)
                return $ans;
        }
        $cur = ($cur * $a) % $m;
    }
    return -1;
}
 
// Driver code
$a = 2;
$b = 3;
$m = 5;
echo discreteLogarithm($a, $b, $m), "\n";
 
$a = 3;
$b = 7;
$m = 11;
echo discreteLogarithm($a, $b, $m);
 
// This code is contributed by ajit.
?>

Javascript

<script>
 
    // Javascript program to calculate
    // discrete logarithm
     
    function discreteLogarithm(a, b, m)
    {
        let n = parseInt(Math.sqrt(m), 10) + 1;
 
        // Calculate a ^ n
        let an = 1;
        for (let i = 0; i < n; ++i)
            an = (an * a) % m;
 
        let value = new Array(m);
        value.fill(0);
 
        // Store all values of a^(n*i) of LHS
        for (let i = 1, cur = an; i<= n; ++i)
        {
            if (value[ cur ] == 0)
                value[ cur ] = i;
            cur = (cur * an) % m;
        }
 
        for (let i = 0, cur = b; i<= n; ++i)
        {
            // Calculate (a ^ j) * b and check
            // for collision
            if (value[cur] > 0)
            {
                let ans = value[cur] * n - i;
                if (ans < m)
                    return ans;
            }
            cur = (cur * a) % m;
        }
        return -1;
    }
     
    let a = 2, b = 3, m = 5;
     
document.write(discreteLogarithm(a, b, m) + "</br>");
   
    a = 3;
    b = 7;
    m = 11;
     
document.write(discreteLogarithm(a, b, m));
 
</script>

Output:

3
-1

Time complexity: O(sqrt(m))
Auxiliary space: O(sqrt(m))
Reference:
http://e-maxx-eng.appspot.com/algebra/discrete-log.html
https://en.wikipedia.org/wiki/Baby-step_giant-step
This article is contributed by Shubham Bansal. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.