AKS Primality Test

There are several primality test available to check whether the number is prime or not like Fermat’s Theorem, Miller-Rabin Primality test and alot more. But problem with all of them is that they all are probabilistic in nature. So, here comes one another method i.e AKS primality test (Agrawal–Kayal–Saxena primality test) and it is deterministically correct for any general number.
Features of AKS primality test :
1. The AKS algorithm can be used to verify the primality of any general number given.
2. The maximum running time of the algorithm can be expressed as a polynomial over the number of digits in the target number.
3. The algorithm is guaranteed to distinguish deterministically whether the target number is prime or composite.
4. The correctness of AKS is not conditional on any subsidiary unproven hypothesis.
The AKS primality test is based upon the following theorem: An integer n greater than 2 is prime if and only if the polynomial congruence relation
$(x+a)^{n}\equiv (x^{n}+a){\pmod {n}}$
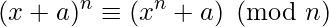
holds for some a coprime to n. Here x is just a formal symbol .
The AKS test evaluates the equality by making complexity dependent on the size of r . This is expressed as
$(x+a)^{n}\equiv (x^{n}+a){\pmod {x^{r}-1, n}}$
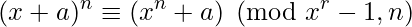
which can be expressed in simpler term as
$(x+a)^{n}-(x^{n}+a)=(x^{r}-1)g+nf$
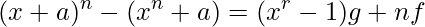
for some polynomials f and g .
This congruence can be checked in polynomial time when r is polynomial to the digits of n. The AKS algorithm evaluates this congruence for a large set of a values, whose size is polynomial to the digits of n. The proof of validity of the AKS algorithm shows that one can find r and a set of a values with the above properties such that if the congruences hold then n is a power of a prime. The brute force approach would require the expansion of the (x – a)^n polynomial and a reduction (mod n) of the resulting n + 1 coefficients .
As a should be co-prime to n. So, to implement this algorithm we can check by taking a = 1, but for large values of n we should take large values of a.
The algorithm is based on the condition that if n is any number, then it is prime if,
( x – 1 )^n – ( x^n – 1) is divisible by n.
Checking for n = 3 :
(x-1)^3 – (x^3 – 1)
= (x^3 – 3x^2 + 3x – 1) – (x^3 – 1)
= -3x^2 + 3x
As all the coefficients are divisible by n i.e. 3, so 3 (n) is prime. As the number increases, size increases.
The code here is based on this condition and can check primes till 64 .
Below is the implementation of above approach:

C++

// C++ code to check if number is prime. This
// program demonstrates concept behind AKS
// algorithm and doesn't implement the actual
// algorithm (This works only till n = 64)
#include <bits/stdc++.h>
using namespace std;
 
// array used to store coefficients .
long long c[100];
 
// function to calculate the coefficients
// of (x - 1)^n - (x^n - 1) with the help
// of Pascal's triangle .
void coef(int n)
{
    c[0] = 1;
    for (int i = 0; i < n; c[0] = -c[0], i++) {
        c[1 + i] = 1;
 
        for (int j = i; j > 0; j--)
            c[j] = c[j - 1] - c[j];
    }
}
 
// function to check whether
// the number is prime or not
bool isPrime(int n)
{
    // Calculating all the coefficients by
    // the function coef and storing all
    // the coefficients in c array .
    coef(n);
 
    // subtracting c[n] and adding c[0] by 1
    // as ( x - 1 )^n - ( x^n - 1), here we
    // are subtracting c[n] by 1 and adding
    // 1 in expression.
    c[0]++, c[n]--;
 
    // checking all the coefficients whether
    // they are divisible by n or not.
    // if n is not prime, then loop breaks
    // and (i > 0).
    int i = n;
    while (i-- && c[i] % n == 0)
        ;
 
    // Return true if all coefficients are
    // divisible by n.
    return i < 0;
}
 
// driver program
int main()
{
    int n = 37;
    if (isPrime(n))
        cout << "Prime" << endl;
    else
        cout << "Not Prime" << endl;
    return 0;
}

Java

// Java code to check if number is prime. This
// program demonstrates concept behind AKS
// algorithm and doesn't implement the actual
// algorithm (This works only till n = 64)
 
class GFG {
    // array used to store coefficients .
    static long c[] = new long[100];
 
    // function to calculate the coefficients
    // of (x - 1)^n - (x^n - 1) with the help
    // of Pascal's triangle .
    static void coef(int n)
    {
        c[0] = 1;
        for (int i = 0; i < n; c[0] = -c[0], i++) {
            c[1 + i] = 1;
 
            for (int j = i; j > 0; j--)
                c[j] = c[j - 1] - c[j];
        }
    }
 
    // function to check whether
    // the number is prime or not
    static boolean isPrime(int n)
    {
        // Calculating all the coefficients by
        // the function coef and storing all
        // the coefficients in c array .
        coef(n);
 
        // subtracting c[n] and adding c[0] by 1
        // as ( x - 1 )^n - ( x^n - 1), here we
        // are subtracting c[n] by 1 and adding
        // 1 in expression.
        c[0]++;
        c[n]--;
 
        // checking all the coefficients whether
        // they are divisible by n or not.
        // if n is not prime, then loop breaks
        // and (i > 0).
        int i = n;
        while ((i--) > 0 && c[i] % n == 0)
            ;
 
        // Return true if all coefficients are
        // divisible by n.
        return i < 0;
    }
    // Driver code
    public static void main(String[] args)
    {
        int n = 37;
        if (isPrime(n))
            System.out.println("Prime");
        else
            System.out.println("Not Prime");
    }
}
 
// This code is contributed by Anant Agarwal.

Python3

# Python3 code to check if
# number is prime. This
# program demonstrates concept
# behind AKS algorithm and
# doesn't implement the actual
# algorithm (This works only
# till n = 64)
 
# array used to
# store coefficients .
c = [0] * 100;
 
# function to calculate the
# coefficients of (x - 1)^n -
# (x^n - 1) with the help
# of Pascal's triangle .
def coef(n):
    c[0] = 1;
    for i in range(n):
        c[1 + i] = 1;
        for j in range(i, 0, -1):
            c[j] = c[j - 1] - c[j];
        c[0] = -c[0];
         
# function to check whether
# the number is prime or not
def isPrime(n):
     
    # Calculating all the coefficients
    # by the function coef and storing
    # all the coefficients in c array .
    coef(n);
     
    # subtracting c[n] and adding
    # c[0] by 1 as ( x - 1 )^n -
    # ( x^n - 1), here we are
    # subtracting c[n] by 1 and
    # adding 1 in expression.
    c[0] = c[0] + 1;
    c[n] = c[n] - 1;
     
    # checking all the coefficients
    # whether they are divisible by
    # n or not. if n is not prime,
    # then loop breaks and (i > 0).
    i = n;
    while (i > -1 and c[i] % n == 0):
        i = i - 1;
     
    # Return true if all coefficients
    # are divisible by n.
    return True if i < 0 else False;
 
# Driver Code
n = 37;
if (isPrime(n)):
    print("Prime");
else:
    print("Not Prime");
     
# This code is contributed by mits

C#

// C# code to check if number is prime. This
// program demonstrates concept behind AKS
// algorithm and doesn't implement the actual
// algorithm (This works only till n = 64)
using System;
 
class GFG {
     
    // array used to store coefficients .
    static long []c = new long[100];
 
    // function to calculate the coefficients
    // of (x - 1)^n - (x^n - 1) with the help
    // of Pascal's triangle .
    static void coef(int n)
    {
        c[0] = 1;
         
        for (int i = 0; i < n; c[0] = -c[0], i++)
        {
            c[1 + i] = 1;
 
            for (int j = i; j > 0; j--)
                c[j] = c[j - 1] - c[j];
        }
    }
 
    // function to check whether
    // the number is prime or not
    static bool isPrime(int n)
    {
         
        // Calculating all the coefficients by
        // the function coef and storing all
        // the coefficients in c array .
        coef(n);
 
        // subtracting c[n] and adding c[0] by 1
        // as ( x - 1 )^n - ( x^n - 1), here we
        // are subtracting c[n] by 1 and adding
        // 1 in expression.
        c[0]++;
        c[n]--;
 
        // checking all the coefficients whether
        // they are divisible by n or not.
        // if n is not prime, then loop breaks
        // and (i > 0).
        int i = n;
        while ((i--) > 0 && c[i] % n == 0)
            ;
 
        // Return true if all coefficients are
        // divisible by n.
        return i < 0;
    }
     
    // Driver code
    public static void Main()
    {
        int n = 37;
        if (isPrime(n))
            Console.WriteLine("Prime");
        else
            Console.WriteLine("Not Prime");
    }
}
 
// This code is contributed by anuj_67.

PHP

<?php
// PHP code to check if number
// is prime. This program
// demonstrates concept behind
// AKS algorithm and doesn't
// implement the actual
// algorithm (This works only
// till n = 64)
 
// array used to
// store coefficients .
global $c;
 
// function to calculate
// the coefficients
// of (x - 1)^n -
// (x^n - 1) with the help
// of Pascal's triangle .
function coef($n)
{
    $c[0] = 1;
    for ($i = 0; $i < $n; $c[0] = -$c[0], $i++)
    {
        $c[1 + $i] = 1;
 
        for ($j = $i; $j > 0; $j--)
            $c[$j] = $c[$j - 1] - $c[$j];
    }
}
 
// function to check whether
// the number is prime or not
function isPrime($n)
{
    global $c;
     
    // Calculating all the
    // coefficients by the
    // function coef and
    // storing all the
    // coefficients in c array .
    coef($n);
 
    // subtracting c[n] and
    // adding c[0] by 1 as
    // ( x - 1 )^n - ( x^n - 1),
    // here we are subtracting c[n]
    // by 1 and adding 1 in expression.
    // $c[0]++; $c[$n]--;
     
    // checking all the coefficients whether
    // they are divisible by n or not.
    // if n is not prime, then loop breaks
    // and (i > 0).
    $i = $n;
    while ($i-- && $c[$i] % $n == 0)
 
    // Return true if all
    // coefficients are
    // divisible by n.
    return $i < 0;
}
 
    // Driver Code
    $n = 37;
    if (isPrime($n))
        echo "Not Prime", "\n";
    else
        echo "Prime", "\n";
 
// This code is contributed by aj_36
?>

Javascript

<script>
 
// Javascript program to check if number is prime.
// This program demonstrates concept behind AKS
// algorithm and doesn't implement the actual
// algorithm (This works only till n = 64)
 
    // array used to store coefficients .
    let c = [];
   
    // function to calculate the coefficients
    // of (x - 1)^n - (x^n - 1) with the help
    // of Pascal's triangle .
    function coef(n)
    {
        c[0] = 1;
        for (let i = 0; i < n; c[0] = -c[0], i++) {
            c[1 + i] = 1;
   
            for (let j = i; j > 0; j--)
                c[j] = c[j - 1] - c[j];
        }
    }
   
    // function to check whether
    // the number is prime or not
    function isPrime(n)
    {
        // Calculating all the coefficients by
        // the function coef and storing all
        // the coefficients in c array .
        coef(n);
   
        // subtracting c[n] and adding c[0] by 1
        // as ( x - 1 )^n - ( x^n - 1), here we
        // are subtracting c[n] by 1 and adding
        // 1 in expression.
        c[0]++;
        c[n]--;
   
        // checking all the coefficients whether
        // they are divisible by n or not.
        // if n is not prime, then loop breaks
        // and (i > 0).
        let i = n;
        while ((i--) > 0 && c[i] % n == 0)
            ;
   
        // Return true if all coefficients are
        // divisible by n.
        return i < 0;
    }
 
// Driver code
 
        let n = 37;
        if (isPrime(n))
            document.write("Prime");
        else
            document.write("Not Prime");
 
</script>