Introduction and Dynamic Programming solution to compute nCr%p

Given three numbers n, r and p, compute value of ⁿC_r mod p. 
Example:

Input:  n = 10, r = 2, p = 13
Output: 6
Explanation: 10C2 is 45 and 45 % 13 is 6.

We strongly recommend that you click here and practice it, before moving on to the solution.

METHOD 1: (Using Dynamic Programming)

A Simple Solution is to first compute ⁿC_r, then compute ⁿC_r % p. This solution works fine when the value of ⁿC_r is small. 
What if the value of ⁿC_r is large?
The value of ⁿC_r%p is generally needed for large values of n when ⁿC_r cannot fit in a variable, and causes overflow. So computing ⁿC_r and then using modular operator is not a good idea as there will be overflow even for slightly larger values of n and r. For example the methods discussed here and here cause overflow for n = 50 and r = 40.
The idea is to compute ⁿC_r using below formula  

   C(n, r) = C(n-1, r-1) + C(n-1, r)
   C(n, 0) = C(n, n) = 1

Working of Above formula and Pascal Triangle:
Let us see how above formula works for C(4, 3)
1==========>> n = 0, C(0, 0) = 1 
1–1========>> n = 1, C(1, 0) = 1, C(1, 1) = 1 
1–2–1======>> n = 2, C(2, 0) = 1, C(2, 1) = 2, C(2, 2) = 1 
1–3–3–1====>> n = 3, C(3, 0) = 1, C(3, 1) = 3, C(3, 2) = 3, C(3, 3)=1 
1–4–6–4–1==>> n = 4, C(4, 0) = 1, C(4, 1) = 4, C(4, 2) = 6, C(4, 3)=4, C(4, 4)=1 
So here every loop on i, builds i’th row of pascal triangle, using (i-1)th row
Extension of above formula for modular arithmetic:
We can use distributive property of modular operator to find nCr % p using above formula.

   C(n, r)%p = [ C(n-1, r-1)%p + C(n-1, r)%p ] % p
   C(n, 0) = C(n, n) = 1

The above formula can be implemented using Dynamic Programming using a 2D array.
The 2D array based dynamic programming solution can be further optimized by constructing one row at a time. See Space optimized version in below post for details.
Binomial Coefficient using Dynamic Programming
Below is implementation based on the space optimized version discussed in above post.  

C++

// A Dynamic Programming based solution to compute nCr % p
#include <bits/stdc++.h>
using namespace std;

// Returns nCr % p
int nCrModp(int n, int r, int p)
{
    // Optimization for the cases when r is large
    if (r > n - r)
        r = n - r;

    // The array C is going to store last row of
    // pascal triangle at the end. And last entry
    // of last row is nCr
    int C[r + 1];
    memset(C, 0, sizeof(C));

    C[0] = 1; // Top row of Pascal Triangle

    // One by constructs remaining rows of Pascal
    // Triangle from top to bottom
    for (int i = 1; i <= n; i++) {

        // Fill entries of current row using previous
        // row values
        for (int j = min(i, r); j > 0; j--)

            // nCj = (n-1)Cj + (n-1)C(j-1);
            C[j] = (C[j] + C[j - 1]) % p;
    }
    return C[r];
}

// Driver program
int main()
{
    int n = 10, r = 2, p = 13;
    cout << "Value of nCr % p is " << nCrModp(n, r, p);
    return 0;
}

JAVA

// A Dynamic Programming based
// solution to compute nCr % p
import java.io.*;
import java.util.*;
import java.math.*;

class GFG {

    // Returns nCr % p
    static int nCrModp(int n, int r, int p)
    {
        if (r > n - r)
            r = n - r;

        // The array C is going to store last
        // row of pascal triangle at the end.
        // And last entry of last row is nCr
        int C[] = new int[r + 1];

        C[0] = 1; // Top row of Pascal Triangle

        // One by constructs remaining rows of Pascal
        // Triangle from top to bottom
        for (int i = 1; i <= n; i++) {

            // Fill entries of current row using previous
            // row values
            for (int j = Math.min(i, r); j > 0; j--)

                // nCj = (n-1)Cj + (n-1)C(j-1);
                C[j] = (C[j] + C[j - 1]) % p;
        }
        return C[r];
    }

    // Driver program
    public static void main(String args[])
    {
        int n = 10, r = 2, p = 13;
        System.out.println("Value of nCr % p is "
                           + nCrModp(n, r, p));
    }
}

// This code is contributed by Nikita Tiwari.

Python3

# A Dynamic Programming based solution to compute nCr % p

# Returns nCr % p
def nCrModp(n, r, p):

    # Optimization for the cases when r is large
    # compared to n-r
    if (r > n- r):
        r = n - r

    # The array C is going to store last row of
    # pascal triangle at the end. And last entry
    # of last row is nCr.
    C = [0 for i in range(r + 1)]

    C[0] = 1 # Top row of Pascal Triangle

    # One by constructs remaining rows of Pascal
    # Triangle from top to bottom
    for i in range(1, n + 1):

        # Fill entries of current row
        # using previous row values
        for j in range(min(i, r), 0, -1):

            # nCj = (n - 1)Cj + (n - 1)C(j - 1)
            C[j] = (C[j] + C[j-1]) % p

    return C[r]

# Driver Program
n = 10
r = 2
p = 13
print('Value of nCr % p is', nCrModp(n, r, p))

# This code is contributed by Soumen Ghosh

C#

// A Dynamic Programming based
// solution to compute nCr % p
using System;

class GFG {

    // Returns nCr % p
    static int nCrModp(int n, int r, int p)
    {

        // Optimization for the cases when r is large
        if (r > n - r)
            r = n - r;

        // The array C is going to store last
        // row of pascal triangle at the end.
        // And last entry of last row is nCr
        int[] C = new int[r + 1];

        for (int i = 0; i < r + 1; i++)
            C[i] = 0;

        C[0] = 1; // Top row of Pascal Triangle

        // One by constructs remaining rows
        // of Pascal Triangle from top to bottom
        for (int i = 1; i <= n; i++) {

            // Fill entries of current row using
            // previous row values
            for (int j = Math.Min(i, r); j > 0; j--)

                // nCj = (n-1)Cj + (n-1)C(j-1);
                C[j] = (C[j] + C[j - 1]) % p;
        }

        return C[r];
    }

    // Driver program
    public static void Main()
    {
        int n = 10, r = 2, p = 13;

        Console.Write("Value of nCr % p is "
                      + nCrModp(n, r, p));
    }
}

// This code is contributed by nitin mittal.

PHP

<?php
// A Dynamic Programming based
// solution to compute nCr % p

// Returns nCr % p
function nCrModp($n, $r, $p)
{

// Optimization for the cases when r is large
if ($r > $n - $r)
    $r = $n - $r;

// The array C is going
// to store last row of
// pascal triangle at
// the end. And last entry
// of last row is nCr
$C = array();

for( $i = 0; $i < $r + 1; $i++)
    $C[$i] = 0;

// Top row of Pascal
// Triangle
$C[0] = 1;

// One by constructs remaining
// rows of Pascal Triangle from
// top to bottom
for ($i = 1; $i <= $n; $i++)
{

    // Fill entries of current
    // row using previous row values
    for ($j = Min($i, $r); $j > 0; $j--)

        // nCj = (n-1)Cj + (n-1)C(j-1);
        $C[$j] = ($C[$j] +
                  $C[$j - 1]) % $p;
}

return $C[$r];
}

// Driver Code
$n = 10; $r = 2;$p = 13;

echo "Value of nCr % p is ",
         nCrModp($n, $r, $p);

// This code is contributed
// by anuj_67.
?>

Javascript

<script>
// A Dynamic Programming based
// solution to compute nCr % p

// Returns nCr % p
function nCrModp(n,r,p)
{
    if (r > n - r)
            r = n - r;

        // The array C is going to store last
        // row of pascal triangle at the end.
        // And last entry of last row is nCr
        let C = new Array(r + 1);
         for(let i = 0; i < r + 1; i++)
            C[i] = 0;
        C[0] = 1; // Top row of Pascal Triangle

        // One by constructs remaining rows of Pascal
        // Triangle from top to bottom
        for (let i = 1; i <= n; i++) {

            // Fill entries of current row using previous
            // row values
            for (let j = Math.min(i, r); j > 0; j--)

                // nCj = (n-1)Cj + (n-1)C(j-1);
                C[j] = (C[j] + C[j - 1]) % p;
        }
        return C[r];
}

// Driver program
let n = 10, r = 2, p = 13;
document.write("Value of nCr % p is "
                   + nCrModp(n, r, p));

// This code is contributed by avanitrachhadiya2155
</script>

Output

Value of nCr % p is 6

Time complexity of above solution is O(n*r) and it requires O(r) space. There are more and better solutions to above problem. 
Compute nCr % p | Set 2 (Lucas Theorem)
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

METHOD 2(Using Pascal Triangle and Dynamic Pro)

Another approach lies in utilizing the concept of the Pascal Triangle. Instead of calculating the ⁿC_r value for every n starting from n=0 till n=n, the approach aims at using the nth row itself for the calculation. The method proceeds by finding out a general relationship between ⁿC_r and ⁿC_r-1.

FORMULA: C(n,r)=C(n,r-1)* (n-r+1)/r

Example:

For instance, take n=5 and r=3.

Input:  n = 5, r = 3, p = 1000000007
Output: 6
Explanation: 5C3 is 10 and 10 % 100000007 is 10.


As per the formula,
C(5,3)=5!/(3!)*(2!)
C(5,3)=10

Also,
C(5,2)=5!/(2!)*(3!)
C(5,2)=10


Let's try applying the above formula.

C(n,r)=C(n,r-1)* (n-r+1)/r
C(5,3)=C(5,2)*(5-3+1)/3
C(5,3)=C(5,2)*1
C(5,3)=10*1

The above example shows that C(n,r) can be easily calculated by calculating C(n,r-1) and multiplying the result with the term (n-r+1)/r. But this multiplication may cause integer overflow for large values of n. To tackle this situation, use modulo multiplication, and modulo division concepts in order to achieve optimizations in terms of integer overflow.

Let’s find out how to build Pascal Triangle for the same.

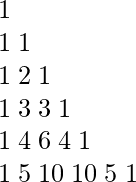
1D array declaration can be further optimized by just the declaration of a single variable to perform calculations. However, integer overflow demands other functions too for the final implementation.

The post below mentions the space and time-optimized implementation for the binary coefficient calculation.

C++

// C++ program to find the nCr%p
// based on optimal Dynamic
// Programming implementation and
// Pascal Triangle concepts
#include <bits/stdc++.h>
using namespace std;

// Returns (a * b) % mod
long long moduloMultiplication(long long a, long long b,
                               long long mod)
{

    // Initialize result
    long long res = 0;

    // Update a if it is more than
    // or equal to mod
    a %= mod;

    while (b) {

        // If b is odd, add a with result
        if (b & 1)
            res = (res + a) % mod;

        // Here we assume that doing 2*a
        // doesn't cause overflow
        a = (2 * a) % mod;
        b >>= 1; // b = b / 2
    }
    return res;
}

// C++ function for extended Euclidean Algorithm
long long int gcdExtended(long long int a, long long int b,
                          long long int* x,
                          long long int* y);

// Function to find modulo inverse of b. It returns
// -1 when inverse doesn't exists
long long int modInverse(long long int b, long long int m)
{

    long long int x, y; // used in extended GCD algorithm
    long long int g = gcdExtended(b, m, &x, &y);

    // Return -1 if b and m are not co-prime
    if (g != 1)
        return -1;

    // m is added to handle negative x
    return (x % m + m) % m;
}

// C++ function for extended Euclidean Algorithm (used to
// find modular inverse.
long long int gcdExtended(long long int a, long long int b,
                          long long int* x,
                          long long int* y)
{

    // Base Case
    if (a == 0) {
        *x = 0, *y = 1;
        return b;
    }

    // To store results of recursive call
    long long int x1, y1;

    long long int gcd = gcdExtended(b % a, a, &x1, &y1);

    // Update x and y using results of recursive
    // call
    *x = y1 - (b / a) * x1;
    *y = x1;
    return gcd;
}

// Function to compute a/b under modulo m
long long int modDivide(long long int a, long long int b,
                        long long int m)
{

    a = a % m;
    long long int inv = modInverse(b, m);
    if (inv == -1)
        // cout << "Division not defined";
        return 0;
    else
        return (inv * a) % m;
}

// Function to calculate nCr % p
int nCr(int n, int r, int p)
{

    // Edge Case which is not possible
    if (r > n)
        return 0;

    // Optimization for the cases when r is large
    if (r > n - r)
        r = n - r;

    // x stores the current result at
    long long int x = 1;

    // each iteration
    // Initialized to 1 as nC0 is always 1.
    for (int i = 1; i <= r; i++) {

        // Formula derived for calculating result is
        // C(n,r-1)*(n-r+1)/r
        // Function calculates x*(n-i+1) % p.
        x = moduloMultiplication(x, (n + 1 - i), p);

        // Function calculates x/i % p.
        x = modDivide(x, i, p);
    }
    return x;
}

// Driver Code
int main()
{

    long long int n = 5, r = 3, p = 1000000007;
    cout << "Value of nCr % p is " << nCr(n, r, p);
    return 0;
}

Java

// Java program to find the nCr%p
// based on optimal Dynamic
// Programming implementation and
// Pascal Triangle concepts
import java.util.*;

class GFG
{

    // Returns (a * b) % mod
    static long moduloMultiplication(long a, long b,
                                     long mod)
    {
        // Initialize result
        long res = 0;

        // Update a if it is more than
        // or equal to mod
        a %= mod;

        while (b > 0) {

            // If b is odd, add a with result
            if ((b & 1) != 0)
                res = (res + a) % mod;

            // Here we assume that doing 2*a
            // doesn't cause overflow
            a = (2 * a) % mod;
            b >>= 1; // b = b / 2
        }
        return res;
    }

    // Global Variables
    static long x, y;

    // Function for extended Euclidean Algorithm
    static long gcdExtended(long a, long b)
    {

        // Base Case
        if (a == 0) {
            x = 0;
            y = 1;
            return b;
        }

        // To store results of recursive call
        long gcd = gcdExtended(b % a, a);
        long x1 = x;
        long y1 = y;

        // Update x and y using results of recursive
        // call
        x = y1 - (b / a) * x1;
        y = x1;

        return gcd;
    }

    static long modInverse(long a, long m)
    {
        long g = gcdExtended(a, m);

        // Return -1 if b and m are not co-prime
        if (g != 1)
            return -1;

        // m is added to handle negative x
        return (x % m + m) % m;
    }

    // Function to compute a/b under modulo m
    static long modDivide(long a, long b, long m)
    {

        a = a % m;
        long inv = modInverse(b, m);
        if (inv == -1)
            return 0;
        else
            return (inv * a) % m;
    }

    // Function to calculate nCr % p
    static long nCr(long n, long r, long p)
    {

        // Edge Case which is not possible
        if (r > n)
            return 0;

        // Optimization for the cases when r is large
        if (r > n - r)
            r = n - r;

        // x stores the current result at
        long x = 1;

        // each iteration
        // Initialized to 1 as nC0 is always 1.
        for (long i = 1L; i <= r; i++) {

            // Formula derived for calculating result is
            // C(n,r-1)*(n-r+1)/r
            // Function calculates x*(n-i+1) % p.
            x = moduloMultiplication(x, (n + 1L - i), p);

            // Function calculates x/i % p.
            x = modDivide(x, i, p);
        }
        return x;
    }

    // Driver Code
    public static void main(String[] args)
    {
        long n = 5, r = 3, p = 1000000007;
        System.out.println("Value of nCr % p is "
                           + nCr(n, r, p));
    }
}

// This code is contributed by phasing17

Python3

# Python3 program to find the nCr%p
# based on optimal Dynamic
# Programming implementation and
# Pascal Triangle concepts

# Returns (a * b) % mod
def moduloMultiplication(a, b, mod):
    # Initialize result
    res = 0

    # Update a if it is more than
    # or equal to mod
    a %= mod

    while (b):

        # If b is odd, add a with result
        if (b & 1):
            res = (res + a) % mod

        # Here we assume that doing 2*a
        # doesn't cause overflow
        a = (2 * a) % mod
        b >>= 1    # b = b / 2

    return res


# Global Variables
x, y = 0, 1

# Function for extended Euclidean Algorithm


def gcdExtended(a, b):
    global x, y

    # Base Case
    if (a == 0):

        x = 0
        y = 1
        return b

    # To store results of recursive call
    gcd = gcdExtended(b % a, a)
    x1 = x
    y1 = y

    # Update x and y using results of recursive
    # call
    x = y1 - int(b / a) * x1
    y = x1

    return gcd


def modInverse(a, m):

    g = gcdExtended(a, m)

    # Return -1 if b and m are not co-prime
    if (g != 1):
        return -1

    # m is added to handle negative x
    return (x % m + m) % m


# Function to compute a/b under modulo m
def modDivide(a, b, m):

    a = a % m
    inv = modInverse(b, m)
    if (inv == -1):
        return 0
    else:
        return (inv * a) % m


# Function to calculate nCr % p
def nCr(n, r, p):

    # Edge Case which is not possible
    if (r > n):
        return 0

    # Optimization for the cases when r is large
    if (r > n - r):
        r = n - r

    # x stores the current result at
    x = 1

    # each iteration
    # Initialized to 1 as nC0 is always 1.
    for i in range(1, r + 1):

        # Formula derived for calculating result is
        # C(n,r-1)*(n-r+1)/r
        # Function calculates x*(n-i+1) % p.
        x = moduloMultiplication(x, (n + 1 - i), p)

        # Function calculates x/i % p.
        x = modDivide(x, i, p)

    return x

# Driver Code
n = 5
r = 3
p = 1000000007
print("Value of nCr % p is ", nCr(n, r, p))

# This code is contributed by phasing17

C#

// C# program to find the nCr%p
// based on optimal Dynamic
// Programming implementation and
// Pascal Triangle concepts
using System;
using System.Collections.Generic;

class GFG
{
  // Returns (a * b) % mod
  static long moduloMultiplication(long a, long b, long mod)
  {
    // Initialize result
    long res = 0;

    // Update a if it is more than
    // or equal to mod
    a %= mod;

    while (b > 0) {

      // If b is odd, add a with result
      if ((b & 1) != 0)
        res = (res + a) % mod;

      // Here we assume that doing 2*a
      // doesn't cause overflow
      a = (2 * a) % mod;
      b >>= 1; // b = b / 2
    }
    return res;
  }

  // Global Variables
  static long x, y;

  // Function for extended Euclidean Algorithm
  static long gcdExtended(long a, long b){

    // Base Case
    if (a == 0)
    {
      x = 0;
      y = 1;
      return b;
    }

    // To store results of recursive call
    long gcd = gcdExtended(b % a, a);
    long x1 = x;
    long y1 = y;

    // Update x and y using results of recursive
    // call
    x = y1 - (b / a) * x1;
    y = x1;

    return gcd;
  }

  static long modInverse(long a, long m)
  {
    long g = gcdExtended(a, m);

    // Return -1 if b and m are not co-prime
    if (g != 1)
      return -1;

    // m is added to handle negative x
    return (x % m + m) % m;
  }

  // Function to compute a/b under modulo m
  static long modDivide(long a, long b, long m)
  {

    a = a % m;
    long inv = modInverse(b, m);
    if (inv == -1)
      return 0;
    else
      return (inv * a) % m;
  }

  // Function to calculate nCr % p
  static long nCr(long n, long r, long p)
  {

    // Edge Case which is not possible
    if (r > n)
      return 0;

    // Optimization for the cases when r is large
    if (r > n - r)
      r = n - r;

    // x stores the current result at
    long x = 1;

    // each iteration
    // Initialized to 1 as nC0 is always 1.
    for (long i = 1L; i <= r; i++) {

      // Formula derived for calculating result is
      // C(n,r-1)*(n-r+1)/r
      // Function calculates x*(n-i+1) % p.
      x = moduloMultiplication(x, (n + 1L - i), p);

      // Function calculates x/i % p.
      x = modDivide(x, i, p);
    }
    return x;
  }

  // Driver Code
  public static void Main(string[] args)
  {
    long n = 5, r = 3, p = 1000000007;
    Console.Write("Value of nCr % p is " + nCr(n, r, p));
  }
}

// This code is contributed by phasing17

Javascript

// JavaScript program to find the nCr%p
// based on optimal Dynamic
// Programming implementation and
// Pascal Triangle concepts

// Returns (a * b) % mod
function moduloMultiplication(a, b, mod)
{
    // Initialize result
    let res = 0;

    // Update a if it is more than
    // or equal to mod
    a %= mod;

    while (b) {

        // If b is odd, add a with result
        if (b & 1)
            res = (res + a) % mod;

        // Here we assume that doing 2*a
        // doesn't cause overflow
        a = (2 * a) % mod;
        b >>= 1; // b = b / 2
    }
    return res;
}

// Global Variables
let x, y;

// Function for extended Euclidean Algorithm
function gcdExtended(a, b){

    // Base Case
    if (a == 0)
    {
        x = 0;
        y = 1;
        return b;
    }

    // To store results of recursive call
    let gcd = gcdExtended(b % a, a);
    let x1 = x;
    let y1 = y;

    // Update x and y using results of recursive
    // call
    x = y1 - Math.floor(b / a) * x1;
    y = x1;

    return gcd;
}

function modInverse(a, m)
{
    let g = gcdExtended(a, m);

    // Return -1 if b and m are not co-prime
    if (g != 1)
        return -1;

    // m is added to handle negative x
    return (x % m + m) % m;
}

// Function to compute a/b under modulo m
function modDivide(a, b, m)
{

    a = a % m;
    let inv = modInverse(b, m);
    if (inv == -1)
        return 0;
    else
        return (inv * a) % m;
}

// Function to calculate nCr % p
function nCr(n, r, p)
{

    // Edge Case which is not possible
    if (r > n)
        return 0;

    // Optimization for the cases when r is large
    if (r > n - r)
        r = n - r;

    // x stores the current result at
    let x = 1;

    // each iteration
    // Initialized to 1 as nC0 is always 1.
    for (var i = 1; i <= r; i++) {

        // Formula derived for calculating result is
        // C(n,r-1)*(n-r+1)/r
        // Function calculates x*(n-i+1) % p.
        x = moduloMultiplication(x, (n + 1 - i), p);

        // Function calculates x/i % p.
        x = modDivide(x, i, p);
    }
    return x;
}

// Driver Code
let n = 5, r = 3, p = 1000000007;
console.log("Value of nCr % p is ", nCr(n, r, p));


// This code is contributed by phasing17

Output

Value of nCr % p is 10

Complexity Analysis:

• The above code needs an extra of O(1) space for the calculations.
• The time involved in the calculation of nCr % p is of the order O(n).

This article is improved by Aryan Gupta. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.