Consider a n x n grid with indexes of top left corner as (0, 0). Dyck path is a staircase walk from bottom left, i.e., (n-1, 0) to top right, i.e., (0, n-1) that lies above the diagonal cells (or cells on line from bottom left to top right).
The task is to count the number of Dyck Paths from (n-1, 0) to (0, n-1).
Examples :
Input : n = 1
Output : 1
Input : n = 2
Output : 2
Input : n = 3
Output : 5
Input : n = 4
Output : 14
The number of Dyck paths from (n-1, 0) to (0, n-1) can be given by the Catalan numberC(n).
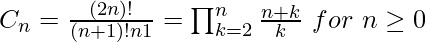
Below are the implementations to find count of Dyck Paths (or n’th Catalan number).
C++
#include<iostream>
using namespace std;
int countDyckPaths(unsigned int n)
{
int res = 1;
for (int i = 0; i < n; ++i)
{
res *= (2 * n - i);
res /= (i + 1);
}
return res / (n+1);
}
int main()
{
int n = 4;
cout << "Number of Dyck Paths is "
<< countDyckPaths(n);
return 0;
}
|
Java
class GFG
{
public static int countDyckPaths(int n)
{
int res = 1;
for (int i = 0; i < n; ++i)
{
res *= (2 * n - i);
res /= (i + 1);
}
return res / (n + 1);
}
public static void main(String args[])
{
int n = 4;
System.out.println("Number of Dyck Paths is " +
countDyckPaths(n));
}
}
|
Python3
def countDyckPaths(n):
res = 1
for i in range(0, n):
res *= (2 * n - i)
res /= (i + 1)
return res / (n+1)
n = 4
print("Number of Dyck Paths is ",
str(int(countDyckPaths(n))))
|
Javascript
<script>
function countDyckPaths(n)
{
let res = 1;
for (let i = 0; i < n; ++i)
{
res *= (2 * n - i);
res /= (i + 1);
}
return res / (n + 1);
}
let n = 4;
document.write("Number of Dyck Paths is " +
countDyckPaths(n));
</script>
|
C#
using System;
class GFG {
static int countDyckPaths(int n)
{
int res = 1;
for (int i = 0; i < n; ++i)
{
res *= (2 * n - i);
res /= (i + 1);
}
return res / (n + 1);
}
public static void Main()
{
int n = 4;
Console.WriteLine("Number of "
+ "Dyck Paths is " +
countDyckPaths(n));
}
}
|
PHP
<?php
function countDyckPaths( $n)
{
$res = 1;
for ( $i = 0; $i < $n; ++$i)
{
$res *= (2 * $n - $i);
$res /= ($i + 1);
}
return $res / ($n + 1);
}
$n = 4;
echo "Number of Dyck Paths is " ,
countDyckPaths($n);
?>
|
OutputNumber of Dyck Paths is 14
Time complexity: O(n).
Auxiliary space: O(1).
Exercise :
- Find number of sequences of 1 and -1 such that every sequence follows below constraints :
a) The length of a sequence is 2n
b) There are equal number of 1’s and -1’s, i.e., n 1’s, n -1s
c) Sum of prefix of every sequence is greater than or equal to 0. For example, 1, -1, 1, -1 and 1, 1, -1, -1 are valid, but -1, -1, 1, 1 is not valid. - Number of paths of length m + n from (m-1, 0) to (0, n-1) that are restricted to east and north steps.
Approach 2:-approach to count the number of Dyck paths –In this implementation, we generate all possible Dyck paths of length n by generating all binary numbers with n bits. We then traverse through each bit in the binary representation of the number and update the depth accordingly. If at any point the depth becomes negative, then the path is not a Dyck path, so we break out of the loop. If we reach the end of the path and the depth is zero, then the path is a Dyck path, so we increment the count. Finally, we return the count of Dyck paths.
C++
#include <iostream>
using namespace std;
int factorial(int n) {
int fact = 1;
for (int i = 1; i <= n; i++) {
fact *= i;
}
return fact;
}
int dyck_paths_2(int n) {
int numerator = factorial(2 * n);
int denominator = factorial(n + 1) * factorial(n);
return numerator / denominator;
}
int main() {
int n = 4;
cout << "Number of Dyck paths is " << n << ": " << dyck_paths_2(n) << endl;
return 0;
}
|
Java
import java.util.*;
public class DyckPaths
{
public static int factorial(int n)
{
int fact = 1;
for (int i = 1; i <= n; i++) {
fact *= i;
}
return fact;
}
public static int dyck_paths_2(int n)
{
int numerator = factorial(2 * n);
int denominator = factorial(n + 1) * factorial(n);
return numerator / denominator;
}
public static void main(String[] args)
{
int n = 4;
System.out.println("Number of Dyck paths is " + n
+ ": " + dyck_paths_2(n));
}
}
|
Python3
def factorial(n):
fact = 1
for i in range(1, n + 1):
fact *= i
return fact
def dyck_paths_2(n):
numerator = factorial(2 * n)
denominator = factorial(n + 1) * factorial(n)
return numerator // denominator
if __name__ == '__main__':
n = 4
print("Number of Dyck paths is {}: {}".format(n, dyck_paths_2(n)))
|
Javascript
function factorial(n) {
let fact = 1;
for (let i = 1; i <= n; i++) {
fact *= i;
}
return fact;
}
function dyckPaths2(n) {
const numerator = factorial(2 * n);
const denominator = factorial(n + 1) * factorial(n);
return numerator / denominator;
}
const n = 4;
console.log(`Number of Dyck paths is ${n}: ${dyckPaths2(n)}`);
|
C#
using System;
class Program {
static int Factorial(int n)
{
int fact = 1;
for (int i = 1; i <= n; i++) {
fact *= i;
}
return fact;
}
static int DyckPaths2(int n)
{
int numerator = Factorial(2 * n);
int denominator = Factorial(n + 1) * Factorial(n);
return numerator / denominator;
}
static void Main(string[] args)
{
int n = 4;
Console.WriteLine("Number of Dyck paths is " + n
+ ": " + DyckPaths2(n));
}
}
|
OutputNumber of Dyck paths is 4: 14
Time complexity: O(n).
Auxiliary space: O(1).
This article is contributed by Aditya Chatterjee. If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above