Cyclic Redundancy Check and Modulo-2 Division
Last Updated :
15 Mar, 2023
CRC or Cyclic Redundancy Check is a method of detecting accidental changes/errors in the communication channel.
CRC uses Generator Polynomial which is available on both sender and receiver side. An example generator polynomial is of the form like x3 + x + 1. This generator polynomial represents key 1011. Another example is x2 + 1 that represents key 101.
n : Number of bits in data to be sent
from sender side.
k : Number of bits in the key obtained
from generator polynomial.
Sender Side (Generation of Encoded Data from Data and Generator Polynomial (or Key)):
- The binary data is first augmented by adding k-1 zeros in the end of the data
- Use modulo-2 binary division to divide binary data by the key and store remainder of division.
- Append the remainder at the end of the data to form the encoded data and send the same
Receiver Side (Check if there are errors introduced in transmission)
Perform modulo-2 division again and if the remainder is 0, then there are no errors.
In this article we will focus only on finding the remainder i.e. check word and the code word.
Modulo 2 Division:
The process of modulo-2 binary division is the same as the familiar division process we use for decimal numbers. Just that instead of subtraction, we use XOR here.
- In each step, a copy of the divisor (or data) is XORed with the k bits of the dividend (or key).
- The result of the XOR operation (remainder) is (n-1) bits, which is used for the next step after 1 extra bit is pulled down to make it n bits long.
- When there are no bits left to pull down, we have a result. The (n-1)-bit remainder which is appended at the sender side.
Illustration:
Example 1 (No error in transmission):
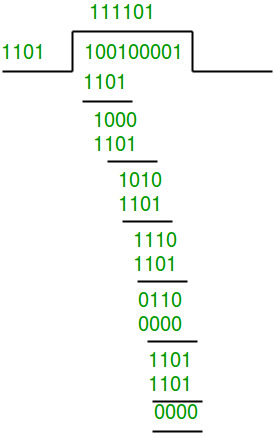
Data word to be sent - 100100
Key - 1101 [ Or generator polynomial x3 + x2 + 1]
Sender Side:

Therefore, the remainder is 001 and hence the encoded
data sent is 100100001.
Receiver Side:
Code word received at the receiver side 100100001
Therefore, the remainder is all zeros. Hence, the
data received has no error.
Example 2: (Error in transmission)
Data word to be sent - 100100
Key - 1101
Sender Side:

Therefore, the remainder is 001 and hence the
code word sent is 100100001.
Receiver Side
Let there be an error in transmission media
Code word received at the receiver side - 100000001

Since the remainder is not all zeroes, the error
is detected at the receiver side.
Implementation:
Below implementation for generating code word from given binary data and key.
C++
#include <bits/stdc++.h>
using namespace std;
string xor1(string a, string b)
{
string result = "";
int n = b.length();
for (int i = 1; i < n; i++) {
if (a[i] == b[i])
result += "0";
else
result += "1";
}
return result;
}
string mod2div(string dividend, string divisor)
{
int pick = divisor.length();
string tmp = dividend.substr(0, pick);
int n = dividend.length();
while (pick < n) {
if (tmp[0] == '1')
tmp = xor1(divisor, tmp) + dividend[pick];
else
tmp = xor1(std::string(pick, '0'), tmp)
+ dividend[pick];
pick += 1;
}
if (tmp[0] == '1')
tmp = xor1(divisor, tmp);
else
tmp = xor1(std::string(pick, '0'), tmp);
return tmp;
}
void encodeData(string data, string key)
{
int l_key = key.length();
string appended_data
= (data + std::string(l_key - 1, '0'));
string remainder = mod2div(appended_data, key);
string codeword = data + remainder;
cout << "Remainder : " << remainder << "\n";
cout << "Encoded Data (Data + Remainder) :" << codeword
<< "\n";
}
void receiver(string data, string key)
{
string currxor
= mod2div(data.substr(0, key.size()), key);
int curr = key.size();
while (curr != data.size()) {
if (currxor.size() != key.size()) {
currxor.push_back(data[curr++]);
}
else {
currxor = mod2div(currxor, key);
}
}
if (currxor.size() == key.size()) {
currxor = mod2div(currxor, key);
}
if (currxor.find('1') != string::npos) {
cout << "there is some error in data" << endl;
}
else {
cout << "correct message received" << endl;
}
}
int main()
{
string data = "100100";
string key = "1101";
cout << "Sender side..." << endl;
encodeData(data, key);
cout << "\nReceiver side..." << endl;
receiver(data+mod2div(data+std::string(key.size() - 1, '0'),key), key);
return 0;
}
|
Java
import java.util.Arrays;
class Program {
static String Xor(String a, String b)
{
String result = "";
int n = b.length();
for (int i = 1; i < n; i++) {
if (a.charAt(i) == b.charAt(i))
result += "0";
else
result += "1";
}
return result;
}
static String Mod2Div(String dividend, String divisor)
{
int pick = divisor.length();
String tmp = dividend.substring(0, pick);
int n = dividend.length();
while (pick < n) {
if (tmp.charAt(0) == '1')
tmp = Xor(divisor, tmp)
+ dividend.charAt(pick);
else
tmp = Xor(new String(new char[pick])
.replace("\0", "0"),
tmp)
+ dividend.charAt(pick);
pick += 1;
}
if (tmp.charAt(0) == '1')
tmp = Xor(divisor, tmp);
else
tmp = Xor(new String(new char[pick])
.replace("\0", "0"),
tmp);
return tmp;
}
static void EncodeData(String data, String key)
{
int l_key = key.length();
String appended_data
= (data
+ new String(new char[l_key - 1])
.replace("\0", "0"));
String remainder = Mod2Div(appended_data, key);
String codeword = data + remainder;
System.out.println("Remainder : " + remainder);
System.out.println(
"Encoded Data (Data + Remainder) :" + codeword
+ "\n");
}
static void Receiver(String data, String key)
{
String currxor
= Mod2Div(data.substring(0, key.length()), key);
int curr = key.length();
while (curr != data.length()) {
if (currxor.length() != key.length()) {
currxor += data.charAt(curr++);
}
else {
currxor = Mod2Div(currxor, key);
}
}
if (currxor.length() == key.length()) {
currxor = Mod2Div(currxor, key);
}
if (currxor.contains("1")) {
System.out.println(
"there is some error in data");
}
else {
System.out.println("correct message received");
}
}
public static void main(String[] args)
{
String data = "100100";
String key = "1101";
System.out.println("\nSender side...");
EncodeData(data, key);
System.out.println("Receiver side...");
Receiver(data+Mod2Div(data+new String(new char[key.length() - 1])
.replace("\0", "0"),key),key);
}
}
|
Python3
def xor(a, b):
result = []
for i in range(1, len(b)):
if a[i] == b[i]:
result.append('0')
else:
result.append('1')
return ''.join(result)
def mod2div(dividend, divisor):
pick = len(divisor)
tmp = dividend[0: pick]
while pick < len(dividend):
if tmp[0] == '1':
tmp = xor(divisor, tmp) + dividend[pick]
else:
tmp = xor('0'*pick, tmp) + dividend[pick]
pick += 1
if tmp[0] == '1':
tmp = xor(divisor, tmp)
else:
tmp = xor('0'*pick, tmp)
checkword = tmp
return checkword
def encodeData(data, key):
l_key = len(key)
appended_data = data + '0'*(l_key-1)
remainder = mod2div(appended_data, key)
codeword = data + remainder
print("Remainder : ", remainder)
print("Encoded Data (Data + Remainder) : ",
codeword)
data = "100100"
key = "1101"
encodeData(data, key)
|
C#
using System;
using System.Linq;
class Program {
static string Xor(string a, string b)
{
string result = "";
int n = b.Length;
for (int i = 1; i < n; i++) {
if (a[i] == b[i])
result += "0";
else
result += "1";
}
return result;
}
static string Mod2Div(string dividend, string divisor)
{
int pick = divisor.Length;
string tmp = dividend.Substring(0, pick);
int n = dividend.Length;
while (pick < n) {
if (tmp[0] == '1')
tmp = Xor(divisor, tmp) + dividend[pick];
else
tmp = Xor(new string('0', pick), tmp)
+ dividend[pick];
pick += 1;
}
if (tmp[0] == '1')
tmp = Xor(divisor, tmp);
else
tmp = Xor(new string('0', pick), tmp);
return tmp;
}
static string EncodeData(string data, string key)
{
int l_key = key.Length;
string appended_data
= (data + new string('0', l_key - 1));
string remainder = Mod2Div(appended_data, key);
string codeword = data + remainder;
Console.WriteLine("Remainder : " + remainder);
Console.WriteLine(
"Encoded Data (Data + Remainder) :" + codeword
+ "\n");
return codeword;
}
static void Receiver(string data, string key)
{
string currxor
= Mod2Div(data.Substring(0, key.Length), key);
int curr = key.Length;
while (curr != data.Length) {
if (currxor.Length != key.Length) {
currxor += data[curr++];
}
else {
currxor = Mod2Div(currxor, key);
}
}
if (currxor.Length == key.Length) {
currxor = Mod2Div(currxor, key);
}
if (currxor.Contains('1')) {
Console.WriteLine(
"there is some error in data");
}
else {
Console.WriteLine("correct message received");
}
}
static void Main(string[] args)
{
string data = "100100";
string key = "1101";
Console.WriteLine("Sender side...");
EncodeData(data, key);
Console.WriteLine("Receiver side...");
Receiver(data+Mod2Div(data + new string('0', key.Length - 1),key), key);
}
}
|
Javascript
<script>
function xor1(a, b)
{
let result = "";
let n = b.length;
for (let i = 1; i < n; i++) {
if (a[i] == b[i]) {
result += "0";
}
else {
result += "1";
}
}
return result;
}
function mod2div(dividend, divisor) {
let pick = divisor.length;
let tmp = dividend.substr(0, pick);
let n = dividend.length;
while (pick < n)
{
if (tmp[0] == '1')
{
tmp = xor1(divisor, tmp) + dividend[pick];
}
else
{
let str = "";
for (let i = 0; i < pick; i++) {
str = str.concat('0');
}
tmp = xor1(str, tmp) + dividend[pick];
}
pick += 1;
}
if (tmp[0] == '1') {
tmp = xor1(divisor, tmp);
}
else {
tmp = xor1(string(pick, '0'), tmp);
}
return tmp;
}
function encodeData(data, key) {
let l_key = key.length;
let str = "";
for (let i = 0; i < l_key - 1; i++) {
str = str.concat('0');
}
console.log(str);
let appended_data = data.concat(str);
let remainder = mod2div(appended_data, key);
let codeword = data + remainder;
document.write("Remainder : ", remainder);
document.write("Encoded Data (Data + Remainder) :", codeword);
}
{
let data = "100100";
let key = "1101";
encodeData(data, key);
}
</script>
|
Output
Sender side...
Remainder : 001
Encoded Data (Data + Remainder) :100100001
Receiver side...
correct message received
Output:
Time Complexity: O(n)
Auxiliary Space: O(n)
Note that CRC is mainly designed and used to protect against common of errors on communication channels and NOT suitable protection against intentional alteration of data (See reasons here)
Implementation using Bit Manipulation:
CRC codeword generation can also be done using bit manipulation methods as follows:
C++
#include <iostream>
#include <math.h>
#include <stdio.h>
using namespace std;
string toBin(long long int num)
{
string bin = "";
while (num) {
if (num & 1)
bin = "1" + bin;
else
bin = "0" + bin;
num = num >> 1;
}
return bin;
}
long long int toDec(string bin)
{
long long int num = 0;
for (int i = 0; i < bin.length(); i++) {
if (bin.at(i) == '1')
num += 1 << (bin.length() - i - 1);
}
return num;
}
void CRC(string dataword, string generator)
{
int l_gen = generator.length();
long long int gen = toDec(generator);
long long int dword = toDec(dataword);
long long int dividend = dword << (l_gen - 1);
int shft = (int)ceill(log2l(dividend + 1)) - l_gen;
long long int rem;
while ((dividend >= gen) || (shft >= 0)) {
rem = (dividend >> shft) ^ gen;
dividend = (dividend & ((1 << shft) - 1))
| (rem << shft);
shft = (int)ceill(log2l(dividend + 1)) - l_gen;
}
long long int codeword
= (dword << (l_gen - 1)) | dividend;
cout << "Remainder: " << toBin(dividend) << endl;
cout << "Codeword : " << toBin(codeword) << endl;
}
int main()
{
string dataword, generator;
dataword = "10011101";
generator = "1001";
CRC(dataword, generator);
return 0;
}
|
Java
class GFG {
static String toBin(int num)
{
String bin = "";
while (num > 0) {
if ((num & 1) != 0)
bin = "1" + bin;
else
bin = "0" + bin;
num = num >> 1;
}
return bin;
}
static int toDec(String bin)
{
int num = 0;
for (int i = 0; i < bin.length(); i++) {
if (bin.charAt(i) == '1')
num += 1 << (bin.length() - i - 1);
}
return num;
}
static void CRC(String dataword, String generator)
{
int l_gen = generator.length();
int gen = toDec(generator);
int dword = toDec(dataword);
int dividend = dword << (l_gen - 1);
int shft = (int)Math.ceil(Math.log(dividend + 1)
/ Math.log(2))
- l_gen;
int rem;
while ((dividend >= gen) || (shft >= 0)) {
rem = (dividend >> shft) ^ gen;
dividend = (dividend & ((1 << shft) - 1))
| (rem << shft);
shft = (int)Math.ceil(Math.log(dividend + 1)
/ Math.log(2))
- l_gen;
}
int codeword = (dword << (l_gen - 1)) | dividend;
System.out.println("Remainder: " + toBin(dividend));
System.out.println("Codeword : " + toBin(codeword));
}
public static void main(String[] args)
{
String dataword, generator;
dataword = "10011101";
generator = "1001";
CRC(dataword, generator);
}
}
|
Python3
from math import log, ceil
def CRC(dataword, generator):
dword = int(dataword, 2)
l_gen = len(generator)
dividend = dword << (l_gen - 1)
shft = ceil(log(dividend + 1, 2)) - l_gen
generator = int(generator, 2)
while dividend >= generator or shft >= 0:
rem = (dividend >> shft) ^ generator
dividend = (dividend & ((1 << shft) - 1)) | (rem << shft)
shft = ceil(log(dividend+1, 2)) - l_gen
codeword = dword << (l_gen-1) | dividend
print("Remainder:", bin(dividend).lstrip("-0b"))
print("Codeword :", bin(codeword).lstrip("-0b"))
dataword = "10011101"
generator = "1001"
CRC(dataword, generator)
|
C#
using System;
class GFG {
static string toBin(int num)
{
string bin = "";
while (num > 0) {
if ((num & 1) != 0)
bin = "1" + bin;
else
bin = "0" + bin;
num = num >> 1;
}
return bin;
}
static int toDec(string bin)
{
int num = 0;
for (int i = 0; i < bin.Length; i++) {
if (bin[i] == '1')
num += 1 << (bin.Length - i - 1);
}
return num;
}
static void CRC(string dataword, string generator)
{
int l_gen = generator.Length;
int gen = toDec(generator);
int dword = toDec(dataword);
int dividend = dword << (l_gen - 1);
int shft = (int)Math.Ceiling(Math.Log(dividend + 1)
/ Math.Log(2))
- l_gen;
int rem = (dividend >> shft) ^ gen;
while ((dividend >= gen) || (shft >= 0)) {
rem = (dividend >> shft) ^ gen;
dividend = (dividend & ((1 << shft) - 1))
| (rem << shft);
shft = (int)Math.Ceiling(Math.Log(dividend + 1)
/ Math.Log(2))
- l_gen;
}
int codeword = (dword << (l_gen - 1)) | dividend;
Console.WriteLine("Remainder: " + toBin(dividend));
Console.WriteLine("Codeword : " + toBin(codeword));
}
public static void Main(string[] args)
{
string dataword, generator;
dataword = "10011101";
generator = "1001";
CRC(dataword, generator);
}
}
|
Javascript
function toBin(num){
var bin = "";
while (num){
if (num & 1)
bin = "1" + bin;
else
bin = "0" + bin;
num = num>>1;
}
return bin;
}
function toDec(bin){
var num = 0;
for (var i=0; i<bin.length; i++){
if (bin[i]=='1')
num += 1 << (bin.length - i - 1);
}
return num;
}
function CRC(dataword, generator){
var l_gen = generator.length;
var gen = toDec(generator);
var dword = toDec(dataword);
var dividend = dword << (l_gen-1);
var shft = Math.ceil(Math.log2(dividend+1)) - l_gen;
var rem;
while ((dividend >= gen) || (shft >= 0)){
rem = (dividend >> shft) ^ gen;
dividend = (dividend & ((1 << shft) - 1)) | (rem << shft);
shft = Math.ceil(Math.log2(dividend + 1)) - l_gen;
}
var codeword = (dword << (l_gen - 1)) | dividend;
console.log( "Remainder:", toBin(dividend));
console.log("Codeword :", toBin(codeword));
}
var dataword = "10011101";
var generator = "1001";
CRC(dataword, generator);
|
Output
Remainder: 100
Codeword : 10011101100
Time Complexity: O(n)
Auxiliary Space: O(n)
References:
https://en.wikipedia.org/wiki/Cyclic_redundancy_check
Share your thoughts in the comments
Please Login to comment...