Introduction and Dynamic Programming solution to compute nCr%p
Last Updated :
23 Apr, 2023
Given three numbers n, r and p, compute value of nCr mod p.
Example:
Input: n = 10, r = 2, p = 13
Output: 6
Explanation: 10C2 is 45 and 45 % 13 is 6.
METHOD 1: (Using Dynamic Programming)
A Simple Solution is to first compute nCr, then compute nCr % p. This solution works fine when the value of nCr is small.
What if the value of nCr is large?
The value of nCr%p is generally needed for large values of n when nCr cannot fit in a variable, and causes overflow. So computing nCr and then using modular operator is not a good idea as there will be overflow even for slightly larger values of n and r. For example the methods discussed here and here cause overflow for n = 50 and r = 40.
The idea is to compute nCr using below formula
C(n, r) = C(n-1, r-1) + C(n-1, r)
C(n, 0) = C(n, n) = 1
Working of Above formula and Pascal Triangle:
Let us see how above formula works for C(4, 3)
1==========>> n = 0, C(0, 0) = 1
1–1========>> n = 1, C(1, 0) = 1, C(1, 1) = 1
1–2–1======>> n = 2, C(2, 0) = 1, C(2, 1) = 2, C(2, 2) = 1
1–3–3–1====>> n = 3, C(3, 0) = 1, C(3, 1) = 3, C(3, 2) = 3, C(3, 3)=1
1–4–6–4–1==>> n = 4, C(4, 0) = 1, C(4, 1) = 4, C(4, 2) = 6, C(4, 3)=4, C(4, 4)=1
So here every loop on i, builds i’th row of pascal triangle, using (i-1)th row
Extension of above formula for modular arithmetic:
We can use distributive property of modular operator to find nCr % p using above formula.
C(n, r)%p = [ C(n-1, r-1)%p + C(n-1, r)%p ] % p
C(n, 0) = C(n, n) = 1
The above formula can be implemented using Dynamic Programming using a 2D array.
The 2D array based dynamic programming solution can be further optimized by constructing one row at a time. See Space optimized version in below post for details.
Binomial Coefficient using Dynamic Programming
Below is implementation based on the space optimized version discussed in above post.
C++
#include <bits/stdc++.h>
using namespace std;
int nCrModp(int n, int r, int p)
{
if (r > n - r)
r = n - r;
int C[r + 1];
memset(C, 0, sizeof(C));
C[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = min(i, r); j > 0; j--)
C[j] = (C[j] + C[j - 1]) % p;
}
return C[r];
}
int main()
{
int n = 10, r = 2, p = 13;
cout << "Value of nCr % p is " << nCrModp(n, r, p);
return 0;
}
|
JAVA
import java.io.*;
import java.util.*;
import java.math.*;
class GFG {
static int nCrModp(int n, int r, int p)
{
if (r > n - r)
r = n - r;
int C[] = new int[r + 1];
C[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = Math.min(i, r); j > 0; j--)
C[j] = (C[j] + C[j - 1]) % p;
}
return C[r];
}
public static void main(String args[])
{
int n = 10, r = 2, p = 13;
System.out.println("Value of nCr % p is "
+ nCrModp(n, r, p));
}
}
|
Python3
def nCrModp(n, r, p):
if (r > n- r):
r = n - r
C = [0 for i in range(r + 1)]
C[0] = 1
for i in range(1, n + 1):
for j in range(min(i, r), 0, -1):
C[j] = (C[j] + C[j-1]) % p
return C[r]
n = 10
r = 2
p = 13
print('Value of nCr % p is', nCrModp(n, r, p))
|
C#
using System;
class GFG {
static int nCrModp(int n, int r, int p)
{
if (r > n - r)
r = n - r;
int[] C = new int[r + 1];
for (int i = 0; i < r + 1; i++)
C[i] = 0;
C[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = Math.Min(i, r); j > 0; j--)
C[j] = (C[j] + C[j - 1]) % p;
}
return C[r];
}
public static void Main()
{
int n = 10, r = 2, p = 13;
Console.Write("Value of nCr % p is "
+ nCrModp(n, r, p));
}
}
|
PHP
<?php
function nCrModp($n, $r, $p)
{
if ($r > $n - $r)
$r = $n - $r;
$C = array();
for( $i = 0; $i < $r + 1; $i++)
$C[$i] = 0;
$C[0] = 1;
for ($i = 1; $i <= $n; $i++)
{
for ($j = Min($i, $r); $j > 0; $j--)
$C[$j] = ($C[$j] +
$C[$j - 1]) % $p;
}
return $C[$r];
}
$n = 10; $r = 2;$p = 13;
echo "Value of nCr % p is ",
nCrModp($n, $r, $p);
?>
|
Javascript
<script>
function nCrModp(n,r,p)
{
if (r > n - r)
r = n - r;
let C = new Array(r + 1);
for(let i = 0; i < r + 1; i++)
C[i] = 0;
C[0] = 1;
for (let i = 1; i <= n; i++) {
for (let j = Math.min(i, r); j > 0; j--)
C[j] = (C[j] + C[j - 1]) % p;
}
return C[r];
}
let n = 10, r = 2, p = 13;
document.write("Value of nCr % p is "
+ nCrModp(n, r, p));
</script>
|
OutputValue of nCr % p is 6
Time complexity of above solution is O(n*r) and it requires O(r) space. There are more and better solutions to above problem.
Compute nCr % p | Set 2 (Lucas Theorem)
METHOD 2(Using Pascal Triangle and Dynamic Pro)
Another approach lies in utilizing the concept of the Pascal Triangle. Instead of calculating the nCr value for every n starting from n=0 till n=n, the approach aims at using the nth row itself for the calculation. The method proceeds by finding out a general relationship between nCr and nCr-1.
FORMULA: C(n,r)=C(n,r-1)* (n-r+1)/r
Example:
For instance, take n=5 and r=3.
Input: n = 5, r = 3, p = 1000000007
Output: 6
Explanation: 5C3 is 10 and 10 % 100000007 is 10.
As per the formula,
C(5,3)=5!/(3!)*(2!)
C(5,3)=10
Also,
C(5,2)=5!/(2!)*(3!)
C(5,2)=10
Let's try applying the above formula.
C(n,r)=C(n,r-1)* (n-r+1)/r
C(5,3)=C(5,2)*(5-3+1)/3
C(5,3)=C(5,2)*1
C(5,3)=10*1
The above example shows that C(n,r) can be easily calculated by calculating C(n,r-1) and multiplying the result with the term (n-r+1)/r. But this multiplication may cause integer overflow for large values of n. To tackle this situation, use modulo multiplication, and modulo division concepts in order to achieve optimizations in terms of integer overflow.
Let’s find out how to build Pascal Triangle for the same.
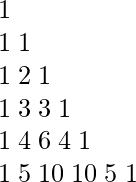
1D array declaration can be further optimized by just the declaration of a single variable to perform calculations. However, integer overflow demands other functions too for the final implementation.
The post below mentions the space and time-optimized implementation for the binary coefficient calculation.
C++
#include <bits/stdc++.h>
using namespace std;
long long moduloMultiplication(long long a, long long b,
long long mod)
{
long long res = 0;
a %= mod;
while (b) {
if (b & 1)
res = (res + a) % mod;
a = (2 * a) % mod;
b >>= 1;
}
return res;
}
long long int gcdExtended(long long int a, long long int b,
long long int* x,
long long int* y);
long long int modInverse(long long int b, long long int m)
{
long long int x, y;
long long int g = gcdExtended(b, m, &x, &y);
if (g != 1)
return -1;
return (x % m + m) % m;
}
long long int gcdExtended(long long int a, long long int b,
long long int* x,
long long int* y)
{
if (a == 0) {
*x = 0, *y = 1;
return b;
}
long long int x1, y1;
long long int gcd = gcdExtended(b % a, a, &x1, &y1);
*x = y1 - (b / a) * x1;
*y = x1;
return gcd;
}
long long int modDivide(long long int a, long long int b,
long long int m)
{
a = a % m;
long long int inv = modInverse(b, m);
if (inv == -1)
return 0;
else
return (inv * a) % m;
}
int nCr(int n, int r, int p)
{
if (r > n)
return 0;
if (r > n - r)
r = n - r;
long long int x = 1;
for (int i = 1; i <= r; i++) {
x = moduloMultiplication(x, (n + 1 - i), p);
x = modDivide(x, i, p);
}
return x;
}
int main()
{
long long int n = 5, r = 3, p = 1000000007;
cout << "Value of nCr % p is " << nCr(n, r, p);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static long moduloMultiplication(long a, long b,
long mod)
{
long res = 0;
a %= mod;
while (b > 0) {
if ((b & 1) != 0)
res = (res + a) % mod;
a = (2 * a) % mod;
b >>= 1;
}
return res;
}
static long x, y;
static long gcdExtended(long a, long b)
{
if (a == 0) {
x = 0;
y = 1;
return b;
}
long gcd = gcdExtended(b % a, a);
long x1 = x;
long y1 = y;
x = y1 - (b / a) * x1;
y = x1;
return gcd;
}
static long modInverse(long a, long m)
{
long g = gcdExtended(a, m);
if (g != 1)
return -1;
return (x % m + m) % m;
}
static long modDivide(long a, long b, long m)
{
a = a % m;
long inv = modInverse(b, m);
if (inv == -1)
return 0;
else
return (inv * a) % m;
}
static long nCr(long n, long r, long p)
{
if (r > n)
return 0;
if (r > n - r)
r = n - r;
long x = 1;
for (long i = 1L; i <= r; i++) {
x = moduloMultiplication(x, (n + 1L - i), p);
x = modDivide(x, i, p);
}
return x;
}
public static void main(String[] args)
{
long n = 5, r = 3, p = 1000000007;
System.out.println("Value of nCr % p is "
+ nCr(n, r, p));
}
}
|
Python3
def moduloMultiplication(a, b, mod):
res = 0
a %= mod
while (b):
if (b & 1):
res = (res + a) % mod
a = (2 * a) % mod
b >>= 1
return res
x, y = 0, 1
def gcdExtended(a, b):
global x, y
if (a == 0):
x = 0
y = 1
return b
gcd = gcdExtended(b % a, a)
x1 = x
y1 = y
x = y1 - int(b / a) * x1
y = x1
return gcd
def modInverse(a, m):
g = gcdExtended(a, m)
if (g != 1):
return -1
return (x % m + m) % m
def modDivide(a, b, m):
a = a % m
inv = modInverse(b, m)
if (inv == -1):
return 0
else:
return (inv * a) % m
def nCr(n, r, p):
if (r > n):
return 0
if (r > n - r):
r = n - r
x = 1
for i in range(1, r + 1):
x = moduloMultiplication(x, (n + 1 - i), p)
x = modDivide(x, i, p)
return x
n = 5
r = 3
p = 1000000007
print("Value of nCr % p is ", nCr(n, r, p))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static long moduloMultiplication(long a, long b, long mod)
{
long res = 0;
a %= mod;
while (b > 0) {
if ((b & 1) != 0)
res = (res + a) % mod;
a = (2 * a) % mod;
b >>= 1;
}
return res;
}
static long x, y;
static long gcdExtended(long a, long b){
if (a == 0)
{
x = 0;
y = 1;
return b;
}
long gcd = gcdExtended(b % a, a);
long x1 = x;
long y1 = y;
x = y1 - (b / a) * x1;
y = x1;
return gcd;
}
static long modInverse(long a, long m)
{
long g = gcdExtended(a, m);
if (g != 1)
return -1;
return (x % m + m) % m;
}
static long modDivide(long a, long b, long m)
{
a = a % m;
long inv = modInverse(b, m);
if (inv == -1)
return 0;
else
return (inv * a) % m;
}
static long nCr(long n, long r, long p)
{
if (r > n)
return 0;
if (r > n - r)
r = n - r;
long x = 1;
for (long i = 1L; i <= r; i++) {
x = moduloMultiplication(x, (n + 1L - i), p);
x = modDivide(x, i, p);
}
return x;
}
public static void Main(string[] args)
{
long n = 5, r = 3, p = 1000000007;
Console.Write("Value of nCr % p is " + nCr(n, r, p));
}
}
|
Javascript
function moduloMultiplication(a, b, mod)
{
let res = 0;
a %= mod;
while (b) {
if (b & 1)
res = (res + a) % mod;
a = (2 * a) % mod;
b >>= 1;
}
return res;
}
let x, y;
function gcdExtended(a, b){
if (a == 0)
{
x = 0;
y = 1;
return b;
}
let gcd = gcdExtended(b % a, a);
let x1 = x;
let y1 = y;
x = y1 - Math.floor(b / a) * x1;
y = x1;
return gcd;
}
function modInverse(a, m)
{
let g = gcdExtended(a, m);
if (g != 1)
return -1;
return (x % m + m) % m;
}
function modDivide(a, b, m)
{
a = a % m;
let inv = modInverse(b, m);
if (inv == -1)
return 0;
else
return (inv * a) % m;
}
function nCr(n, r, p)
{
if (r > n)
return 0;
if (r > n - r)
r = n - r;
let x = 1;
for (var i = 1; i <= r; i++) {
x = moduloMultiplication(x, (n + 1 - i), p);
x = modDivide(x, i, p);
}
return x;
}
let n = 5, r = 3, p = 1000000007;
console.log("Value of nCr % p is ", nCr(n, r, p));
|
OutputValue of nCr % p is 10
Complexity Analysis:
- The above code needs an extra of O(1) space for the calculations.
- The time involved in the calculation of nCr % p is of the order O(n).
This article is improved by Aryan Gupta.
Share your thoughts in the comments
Please Login to comment...