Program for Muller Method
Last Updated :
27 Aug, 2022
Given a function f(x) on floating number x and three initial distinct guesses for root of the function, find the root of function. Here, f(x) can be an algebraic or transcendental function.
Examples:
Input : A function f(x) = x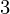 + 2x
+ 2x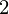 + 10x - 20 and three initial guesses - 0, 1 and 2 .Output : The value of the root is 1.3688 or any other value within permittable deviation from the root. Input : A function f(x) = x
+ 10x - 20 and three initial guesses - 0, 1 and 2 .Output : The value of the root is 1.3688 or any other value within permittable deviation from the root. Input : A function f(x) = x - 5x + 2 and three initial guesses - 0, 1 and 2 .Output :The value of the root is 0.4021 or any other value within permittable deviation from the root.
- 5x + 2 and three initial guesses - 0, 1 and 2 .Output :The value of the root is 0.4021 or any other value within permittable deviation from the root.
Muller Method
Muller Method is a root-finding algorithm for finding the root of a equation of the form, f(x)=0. It was discovered by David E. Muller in 1956.
It begins with three initial assumptions of the root, and then constructing a parabola through these three points, and takes the intersection of the x-axis with the parabola to be the next approximation. This process continues until a root with the desired level of accuracy is found .
Why to learn Muller’s Method?
Muller Method, being one of the root-finding method along with the other ones like Bisection Method, Regula – Falsi Method, Secant Method and Newton – Raphson Method. But, it offers certain advantages over these methods, as follows –
- The rate of convergence, i.e., how much closer we move to the root at each step, is approximately 1.84 in Muller Method, whereas it is 1.62 for secant method, and linear, i.e., 1 for both Regula – falsi Method and bisection method . So, Muller Method is faster than Bisection, Regula – Falsi and Secant method.
- Although, it is slower than Newton – Raphson’s Method, which has a rate of convergence of 2, but it overcomes one of the biggest drawbacks of Newton-Raphson Method, i.e., computation of derivative at each step.
So, this shows that Muller Method is an efficient method in calculating root of the function.
Algorithm And Its Working
- Assume any three distinct initial roots of the function, let it be x0, x1 and x2.
- Now, draw a second degree polynomial, i.e., a parabola, through the values of function f(x) for these points – x0, x1 and x2.
The equation of the parabola, p(x), through these points is as follows-
p(x) = c + b(x – x ) + a(x – x
) + a(x – x )
)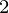 , where a, b and c are constants.
, where a, b and c are constants.
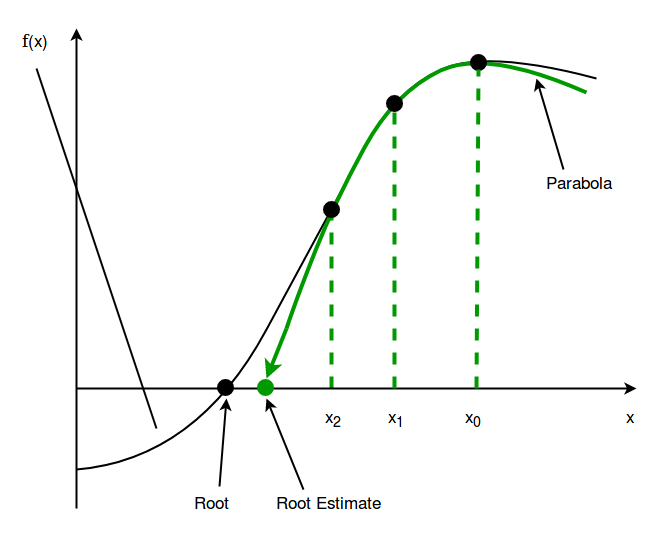
- After drawing the parabola, then find the intersection of this parabola with the x-axis, let us say x3 .
- Finding the intersection of parabola with the x-axis, i.e., x3:
- To find x
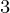 , the root of p(x), where p(x) = c + b(x – x
, the root of p(x), where p(x) = c + b(x – x ) + a(x – x
) + a(x – x )
)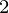 , such that p(x
, such that p(x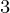 ) = c + b(x
) = c + b(x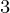 – x
– x ) + a(x
) + a(x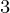 – x
– x )
)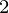 = 0, apply the quadratic formula to p(x).Since, there will be two roots, but we have to take that one which is closer to x
= 0, apply the quadratic formula to p(x).Since, there will be two roots, but we have to take that one which is closer to x .To avoid round-off errors due to subtraction of nearby equal numbers, use the following equation:
.To avoid round-off errors due to subtraction of nearby equal numbers, use the following equation:
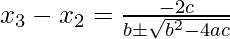
Now, since, root of p(x) has to be closer to x , so we have to take that value which has a greater denominator out of the two values possible from the above equation.
, so we have to take that value which has a greater denominator out of the two values possible from the above equation. - To find a, b and c for the above equation, put x in p(x) as x
 , x
, x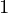 and x
and x , and let these values be p(x
, and let these values be p(x ), p(x
), p(x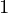 ) and p(x
) and p(x ), which are as follows-
), which are as follows-
p(x ) = c + b(x
) = c + b(x – x
– x ) + a(x
) + a(x – x
– x )
)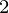 = f(x
= f(x ).
).
p(x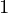 ) = c + b(x
) = c + b(x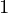 – x
– x ) + a(x
) + a(x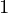 – x
– x )
)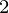 = f(x
= f(x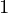 ).
).
p(x ) = c + b(x
) = c + b(x – x
– x ) + a(x
) + a(x – x
– x )
)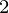 = c = f(x
= c = f(x ).
).
- So, we have three equations and three variables – a, b, c. After solving them to found out the values of these variables, we get the following values of a, b and c-
c = p(x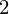 ) = f(x
) = f(x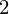 ) .b = (d
) .b = (d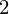 *(h
*(h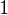 )
)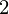 - d
- d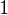 *(h
*(h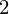 )
)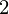 ) / ( h
) / ( h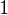 h
h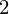 * (h
* (h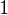 - h
- h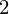 )) .a = (d
)) .a = (d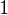 *(h
*(h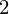 ) - d
) - d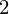 *(h
*(h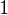 )) / ( h
)) / ( h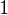 h
h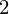 * (h
* (h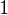 - h
- h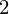 )).
)).
where,
d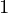 = p(x
= p(x ) – p(x
) – p(x ) = f(x
) = f(x ) – f(x
) – f(x )
)
d = p(x
= p(x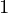 ) – p(x
) – p(x ) = f(x
) = f(x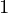 ) – f(x
) – f(x )
)
h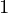 = x
= x – x
– x
h = x
= x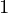 – x
– x
- Now, put these values in the expression for x
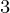 – x
– x , and obtain x
, and obtain x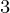 .
.
This is how root of p(x) = x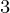 is obtained.
is obtained.
- If x
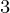 is very close to x
is very close to x within the permittable error, then x
within the permittable error, then x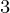 becomes the root of f(x), otherwise, keep repeating the process of finding the next x
becomes the root of f(x), otherwise, keep repeating the process of finding the next x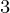 , with previous x
, with previous x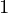 , x
, x and x
and x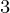 as the new x
as the new x , x
, x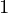 and x
and x .
.
C++
#include<bits/stdc++.h>
using namespace std;
const int MAX_ITERATIONS = 10000;
float f(float x)
{
return 1*pow(x, 3) + 2*x*x + 10*x - 20;
}
void Muller(float a, float b, float c)
{
int i;
float res;
for (i = 0;;++i)
{
float f1 = f(a);
float f2 = f(b);
float f3 = f(c);
float d1 = f1 - f3;
float d2 = f2 - f3;
float h1 = a - c;
float h2 = b - c;
float a0 = f3;
float a1 = (((d2*pow(h1, 2)) - (d1*pow(h2, 2)))
/ ((h1*h2) * (h1-h2)));
float a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2)));
float x = ((-2*a0) / (a1 + abs(sqrt(a1*a1-4*a0*a2))));
float y = ((-2*a0) / (a1-abs(sqrt(a1*a1-4*a0*a2))));
if (x >= y)
res = x + c;
else
res = y + c;
float m = res*100;
float n = c*100;
m = floor(m);
n = floor(n);
if (m == n)
break;
a = b;
b = c;
c = res;
if (i > MAX_ITERATIONS)
{
cout << "Root cannot be found using"
<< " Muller's method";
break;
}
}
if (i <= MAX_ITERATIONS)
cout << "The value of the root is " << res;
}
int main()
{
float a = 0, b = 1, c = 2;
Muller(a, b, c);
return 0;
}
|
Java
import java.io.*;
import static java.lang.Math.*;
class Muller
{
static final int MAX_ITERATIONS = 10000;
static double f(double x)
{
return 1*pow(x, 3) + 2*x*x + 10*x - 20;
}
static void Muller(double a, double b, double c)
{
int i;
double res;
for (i = 0;; ++i)
{
double f1 = f(a);
double f2 = f(b);
double f3 = f(c);
double d1 = f1 - f3;
double d2 = f2 - f3;
double h1 = a - c;
double h2 = b - c;
double a0 = f3;
double a1 = (((d2*pow(h1, 2)) - (d1*pow(h2, 2)))
/ ((h1*h2) * (h1-h2)));
double a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2)));
double x = ((-2*a0)/(a1 + abs(sqrt(a1*a1-4*a0*a2))));
double y = ((-2*a0)/(a1-abs(sqrt(a1*a1-4*a0*a2))));
if (x >= y)
res = x + c;
else
res = y + c;
double m = res*100;
double n = c*100;
m = floor(m);
n = floor(n);
if (m == n)
break;
a = b;
b = c;
c = res;
if (i > MAX_ITERATIONS)
{
System.out.println("Root cannot be found using" +
" Muller's method");
break;
}
}
if (i <= MAX_ITERATIONS)
System.out.println("The value of the root is " + res);
}
public static void main(String args[])
{
double a = 0, b = 1, c = 2;
Muller(a, b, c);
}
}
|
Python3
import math;
MAX_ITERATIONS = 10000;
def f(x):
return (1 * pow(x, 3) + 2 * x * x +
10 * x - 20);
def Muller(a, b, c):
res = 0;
i = 0;
while (True):
f1 = f(a); f2 = f(b); f3 = f(c);
d1 = f1 - f3;
d2 = f2 - f3;
h1 = a - c;
h2 = b - c;
a0 = f3;
a1 = (((d2 * pow(h1, 2)) -
(d1 * pow(h2, 2))) /
((h1 * h2) * (h1 - h2)));
a2 = (((d1 * h2) - (d2 * h1)) /
((h1 * h2) * (h1 - h2)));
x = ((-2 * a0) / (a1 +
abs(math.sqrt(a1 * a1 - 4 * a0 * a2))));
y = ((-2 * a0) / (a1 -
abs(math.sqrt(a1 * a1 - 4 * a0 * a2))));
if (x >= y):
res = x + c;
else:
res = y + c;
m = res * 100;
n = c * 100;
m = math.floor(m);
n = math.floor(n);
if (m == n):
break;
a = b;
b = c;
c = res;
if (i > MAX_ITERATIONS):
print("Root cannot be found using",
"Muller's method");
break;
i += 1;
if (i <= MAX_ITERATIONS):
print("The value of the root is",
round(res, 4));
a = 0;
b = 1;
c = 2;
Muller(a, b, c);
|
C#
using System;
class Muller1
{
static int MAX_ITERATIONS = 10000;
static double f(double x)
{
return 1*Math.Pow(x, 3) + 2*x*x + 10*x - 20;
}
static void Muller(double a, double b, double c)
{
int i;
double res;
for (i = 0;; ++i)
{
double f1 = f(a);
double f2 = f(b);
double f3 = f(c);
double d1 = f1 - f3;
double d2 = f2 - f3;
double h1 = a - c;
double h2 = b - c;
double a0 = f3;
double a1 = (((d2*Math.Pow(h1, 2)) - (d1*Math.Pow(h2, 2)))
/ ((h1*h2) * (h1-h2)));
double a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2)));
double x = ((-2*a0)/(a1 + Math.Abs(Math.Sqrt(a1*a1-4*a0*a2))));
double y = ((-2*a0)/(a1-Math.Abs(Math.Sqrt(a1*a1-4*a0*a2))));
if (x >= y)
res = x + c;
else
res = y + c;
double m = res*100;
double n = c*100;
m = Math.Floor(m);
n = Math.Floor(n);
if (m == n)
break;
a = b;
b = c;
c = res;
if (i > MAX_ITERATIONS)
{
Console.WriteLine("Root cannot be found using" +
" Muller's method");
break;
}
}
if (i <= MAX_ITERATIONS)
Console.WriteLine("The value of the root is " + Math.Round(res,4));
}
static void Main()
{
double a = 0, b = 1, c = 2;
Muller(a, b, c);
}
}
|
PHP
<?php
$MAX_ITERATIONS = 10000;
function f($x)
{
return 1*pow($x, 3) + 2*$x*$x + 10*$x - 20;
}
function Muller($a, $b, $c)
{
global $MAX_ITERATIONS;
$res=0;
for ($i = 0;;++$i)
{
$f1 = f($a);
$f2 = f($b);
$f3 = f($c);
$d1 = $f1 - $f3;
$d2 = $f2 - $f3;
$h1 = $a - $c;
$h2 = $b - $c;
$a0 = $f3;
$a1 = ((($d2*pow($h1, 2)) - ($d1*pow($h2, 2)))
/ (($h1*$h2) * ($h1-$h2)));
$a2 = ((($d1*$h2) - ($d2*$h1))/(($h1*$h2) * ($h1-$h2)));
$x = ((-2*$a0) / ($a1 + abs(sqrt($a1*$a1-4*$a0*$a2))));
$y = ((-2*$a0) / ($a1-abs(sqrt($a1*$a1-4*$a0*$a2))));
if ($x >= $y)
$res = $x + $c;
else
$res = $y + $c;
$m = $res*100;
$n = $c*100;
$m = floor($m);
$n = floor($n);
if ($m == $n)
break;
$a = $b;
$b = $c;
$c = $res;
if ($i > $MAX_ITERATIONS)
{
echo"Root cannot be found using Muller's method";
break;
}
}
if ($i <= $MAX_ITERATIONS)
echo "The value of the root is ".round($res,4);
}
$a = 0;
$b = 1;
$c = 2;
Muller($a, $b, $c);
?>
|
Javascript
<script>
const MAX_ITERATIONS = 10000;
function f(x)
{
return 1*Math.pow(x, 3) + 2*x*x + 10*x - 20;
}
function Muller(a, b, c)
{
let i;
let res;
for (i = 0;;++i)
{
let f1 = f(a);
let f2 = f(b);
let f3 = f(c);
let d1 = f1 - f3;
let d2 = f2 - f3;
let h1 = a - c;
let h2 = b - c;
let a0 = f3;
let a1 = (((d2*Math.pow(h1, 2)) - (d1*Math.pow(h2, 2)))
/ ((h1*h2) * (h1-h2)));
let a2 = (((d1*h2) - (d2*h1))/((h1*h2) * (h1-h2)));
let x = ((-2*a0) / (a1 + Math.abs(Math.sqrt(a1*a1-4*a0*a2))));
let y = ((-2*a0) / (a1-Math.abs(Math.sqrt(a1*a1-4*a0*a2))));
if (x >= y)
res = x + c;
else
res = y + c;
let m = res*100;
let n = c*100;
m = Math.floor(m);
n = Math.floor(n);
if (m == n)
break;
a = b;
b = c;
c = res;
if (i > MAX_ITERATIONS)
{
document.write("Root cannot be found using"
+ " Muller's method");
break;
}
}
if (i <= MAX_ITERATIONS)
document.write("The value of the root is " + res.toFixed(4));
}
let a = 0, b = 1, c = 2;
Muller(a, b, c);
</script>
|
Output:
The value of the root is 1.3688
Auxiliary Space: O(1)
Advantages
- Can find imaginary roots.
- No need to find derivatives.
Disadvantages
- Long to do by hand, more room for error.
- Extraneous roots can be found.
Reference-
- Higher Engineer Mathematics by B.S. Grewal.
Share your thoughts in the comments
Please Login to comment...