Given a function f(x) on floating number x and an initial guess for root, find root of function in interval. Here f(x) represents algebraic or transcendental equation.
For simplicity, we have assumed that derivative of function is also provided as input.
Example:
Input: A function of x (for example x3 – x2 + 2),
derivative function of x (3x2 – 2x for above example)
and an initial guess x0 = -20
Output: The value of root is : -1.00
OR any other value close to root.We have discussed below methods to find root in set 1 and set 2
Set 1: The Bisection Method
Set 2: The Method Of False Position
Comparison with above two methods:
- In previous methods, we were given an interval. Here we are required an initial guess value of root.
- The previous two methods are guaranteed to converge, Newton Raphson may not converge in some cases.
- Newton Raphson method requires derivative. Some functions may be difficult to
impossible to differentiate. - For many problems, Newton Raphson method converges faster than the above two methods.
- Also, it can identify repeated roots, since it does not look for changes in the sign of f(x) explicitly
The formula:
Starting from initial guess x1, the Newton Raphson method uses below formula to find next value of x, i.e., xn+1 from previous value xn.
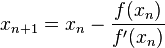
Advantages of Newton Raphson Method:
- It is best method to solve the non-linear equations.
- It can also be used to solve the system of non-linear equations, non-linear differential and non-linear integral equations.
- The order of convergence is quadric i.e. of second order which makes this method fast as compared to other methods.
- It is very easy to implement on computer.
Disadvantages of Newton Raphson Method:
- This method becomes complicated if the derivative of the function f(x) is not simple.
- This method requires a great and sensitive attention regarding the choice of its approximation.
- In each iteration, we have to evaluate two quantities f(x) and f'(x) for some x.
Algorithm:
Input: initial x, func(x), derivFunc(x)
Output: Root of Func()
- Compute values of func(x) and derivFunc(x) for given initial x
- Compute h: h = func(x) / derivFunc(x)
- While h is greater than allowed error ε
- h = func(x) / derivFunc(x)
- x = x – h
Below is the implementation of above algorithm.
C++
#include<bits/stdc++.h>
#define EPSILON 0.001
using namespace std;
double func(double x)
{
return x*x*x - x*x + 2;
}
double derivFunc(double x)
{
return 3*x*x - 2*x;
}
void newtonRaphson(double x)
{
double h = func(x) / derivFunc(x);
while (abs(h) >= EPSILON)
{
h = func(x)/derivFunc(x);
x = x - h;
}
cout << "The value of the root is : " << x;
}
int main()
{
double x0 = -20;
newtonRaphson(x0);
return 0;
}
|
Java
class GFG {
static final double EPSILON = 0.001;
static double func(double x)
{
return x * x * x - x * x + 2;
}
static double derivFunc(double x)
{
return 3 * x * x - 2 * x;
}
static void newtonRaphson(double x)
{
double h = func(x) / derivFunc(x);
while (Math.abs(h) >= EPSILON)
{
h = func(x) / derivFunc(x);
x = x - h;
}
System.out.print("The value of the"
+ " root is : "
+ Math.round(x * 100.0) / 100.0);
}
public static void main (String[] args)
{
double x0 = -20;
newtonRaphson(x0);
}
}
|
Python3
def func( x ):
return x * x * x - x * x + 2
def derivFunc( x ):
return 3 * x * x - 2 * x
def newtonRaphson( x ):
h = func(x) / derivFunc(x)
while abs(h) >= 0.0001:
h = func(x)/derivFunc(x)
x = x - h
print("The value of the root is : ",
"%.4f"% x)
x0 = -20
newtonRaphson(x0)
|
C#
using System;
class GFG {
static double EPSILON = 0.001;
static double func(double x)
{
return x * x * x - x * x + 2;
}
static double derivFunc(double x)
{
return 3 * x * x - 2 * x;
}
static void newtonRaphson(double x)
{
double h = func(x) / derivFunc(x);
while (Math.Abs(h) >= EPSILON)
{
h = func(x) / derivFunc(x);
x = x - h;
}
Console.Write("The value of the"
+ " root is : "
+ Math.Round(x * 100.0) / 100.0);
}
public static void Main ()
{
double x0 = -20;
newtonRaphson(x0);
}
}
|
PHP
<?php
$EPSILON = 0.001;
function func($x)
{
return $x * $x * $x -
$x * $x + 2;
}
function derivFunc($x)
{
return 3 * $x *
$x - 2 * $x;
}
function newtonRaphson($x)
{
global $EPSILON;
$h = func($x) / derivFunc($x);
while (abs($h) >= $EPSILON)
{
$h = func($x) / derivFunc($x);
$x = $x - $h;
}
echo "The value of the ".
"root is : " , $x;
}
$x0 = -20;
newtonRaphson($x0);
?>
|
Javascript
<script>
let EPSILON = 0.001;
function func(x)
{
return x * x * x - x * x + 2;
}
function derivFunc(x)
{
return 3 * x * x - 2 * x;
}
function newtonRaphson(x)
{
let h = func(x) / derivFunc(x);
while (Math.abs(h) >= EPSILON)
{
h = func(x) / derivFunc(x);
x = x - h;
}
document.write("The value of the"
+ " root is : "
+ Math.round(x * 100.0) / 100.0);
}
let x0 = -20;
newtonRaphson(x0);
</script>
|
Output:
The value of root is : -1.00
How does this work?
The idea is to draw a line tangent to f(x) at point x1. The point where the tangent line crosses the x axis should be a better estimate of the root than x1. Call this point x2. Calculate f(x2), and draw a line tangent at x2.
We know that slope of line from (x1, f(x1)) to (x2, 0) is f'(x1)) where f’ represents derivative of f.
f'(x1) = (0 - f(x1)) / (x2 - x1)
f'(x1) * (x2 - x1) = - f(x1)
x2 = x1 - f(x1) / f'(x1)
By finding this point 'x2', we move closer towards the root.
We have to keep on repeating the above step till we get really close to
the root or we find it.
In general,
xn+1 = xn - f(xn) / f'(xn)
Alternate Explanation using Taylor’s Series:
Let x1 be the initial guess.
We can write x2 as below:
xn+1 = xn + h ------- (1)
Here h would be a small value that can be positive or negative.
According to Taylor's Series,
ƒ(x) that is infinitely differentiable can be written as below
f(xn+1) = f(xn + h)
= f(xn) + h*f'(xn) + ((h*h)/2!)*(f''(xn)) + ...
Since we are looking for root of function, f(xn+1) = 0
f(xn) + h*f'(xn) + ((h*h)/2!)*(f''(xn)) + ... = 0
Now since h is small, h*h would be very small.
So if we ignore higher order terms, we get
f(xn) + h*f'(xn) = 0
Substituting this value of h = xn+1 - xn from equation (1) we get,
f(xn) + (xn+1 - xn)*f'(xn) = 0
xn+1 = xn - f(xn) / f'(xn) Notes:
- We generally used this method to improve the result obtained by either bisection method or method of false position.
- Babylonian method for square root is derived from the Newton-Raphson method.
References:
Introductory Methods of Numerical Analysis by S.S. Sastry
https://en.wikipedia.org/wiki/Newton’s_method
http://www.cae.tntech.edu/Members/renfro/me2000/lectures/2004-09-07_handouts.pdf/at_download/file
This article is contributed by Abhiraj Smit. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above