Finding power of prime number p in n!
Last Updated :
23 Jun, 2022
Given a number ‘n’ and a prime number ‘p’. We need to find out the power of ‘p’ in the prime factorization of n!
Examples:
Input : n = 4, p = 2
Output : 3
Power of 2 in the prime factorization
of 2 in 4! = 24 is 3
Input : n = 24, p = 2
Output : 22
Naive approach
The naive approach is to find the power of p in each number from 1 to n and add them. Because we know that during multiplication power is added.
C++
#include <bits/stdc++.h>
using namespace std;
int PowerOFPINnfactorial(int n, int p)
{
int ans = 0;
int temp = p;
while (temp <= n) {
ans += n / temp;
temp = temp * p;
}
return ans;
}
int main()
{
cout << PowerOFPINnfactorial(4, 2) << endl;
return 0;
}
|
Java
public class GFG
{
static int PowerOFPINnfactorial(int n, int p)
{
int ans = 0;
for (int i = 1; i <= n; i++) {
int count = 0, temp = i;
while (temp % p == 0) {
count++;
temp = temp / p;
}
ans += count;
}
return ans;
}
public static void main(String[] args)
{
System.out.println(PowerOFPINnfactorial(4, 2));
}
}
|
Python3
def PowerOFPINnfactorial(n, p):
ans = 0;
temp = p;
while (temp <= n):
ans += n / temp;
temp = temp * p;
return ans;
print(PowerOFPINnfactorial(4, 2));
|
C#
using System;
public class GFG
{
static int PowerOFPINnfactorial(int n, int p)
{
int ans = 0;
for (int i = 1; i <= n; i++) {
int count = 0, temp = i;
while (temp % p == 0) {
count++;
temp = temp / p;
}
ans += count;
}
return ans;
}
public static void Main(String []args)
{
Console.WriteLine(PowerOFPINnfactorial(4, 2));
}
}
|
PHP
<?php
function PowerOFPINnfactorial($n, $p)
{
$ans = 0;
$temp = $p;
while ($temp <= $n)
{
$ans += $n / $temp;
$temp = $temp * $p;
}
return $ans;
}
echo PowerOFPINnfactorial(4, 2) . "\n";
?>
|
Javascript
<script>
function PowerOFPINnfactorial(n, p)
{
let ans = 0;
let temp = p;
while (temp <= n)
{
ans += n / temp;
temp = temp * p;
}
return ans;
}
document.write(PowerOFPINnfactorial(4, 2));
</script>
|
Kotlin
fun PowerOFPINnfactorial(n: Int, p: Int)
{
var ans = 0;
var temp = p;
while(temp<=n)
{
ans+=n/temp;
temp*=p;
}
println(ans)
}
fun main(args: Array<String>)
{
val n = 4
val p = 2
PowerOFPINnfactorial(n,p)
}
|
Output:
3
Time Complexity: O(logpn)
Auxiliary Space: O(1)
Efficient Approach
Before discussing efficient approach lets discuss a question given a two numbers n, m how many numbers are there from 1 to n that are divisible by m the answer is floor(n/m).
Now coming back to our original question to find the power of p in n! what we do is count the number of numbers from 1 to n that are divisible by p then by 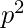 then by
then by 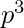 till
till 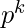 > n and add them. This will be our required answer.
> n and add them. This will be our required answer.
Powerofp(n!) = floor(n/p) + floor(n/p^2) + floor(n/p^3)........
Below is the implementation of the above steps.
C++
#include <bits/stdc++.h>
using namespace std;
int PowerOFPINnfactorial(int n, int p)
{
int ans = 0;
int temp = p;
while (temp <= n) {
ans += n / temp;
temp = temp * p;
}
return ans;
}
int main()
{
cout << PowerOFPINnfactorial(4, 2) << endl;
return 0;
}
|
Java
public class GFG
{
static int PowerOFPINnfactorial(int n, int p)
{
int ans = 0;
int temp = p;
while (temp <= n) {
ans += n / temp;
temp = temp * p;
}
return ans;
}
public static void main(String[] args)
{
System.out.println(PowerOFPINnfactorial(4, 2));
}
}
|
Python3
def PowerOFPINnfactorial(n, p):
ans = 0
temp = p
while (temp <= n) :
ans += n / temp
temp = temp * p
return int(ans)
print(PowerOFPINnfactorial(4, 2))
|
C#
using System;
public class GFG
{
static int PowerOFPINnfactorial(int n, int p)
{
int ans = 0;
int temp = p;
while (temp <= n) {
ans += n / temp;
temp = temp * p;
}
return ans;
}
public static void Main(String []args)
{
Console.WriteLine(PowerOFPINnfactorial(4, 2));
}
}
|
PHP
<?php
function PowerOFPINnfactorial($n, $p)
{
$ans = 0;
$temp = $p;
while ($temp <= $n)
{
$ans += $n / $temp;
$temp = $temp * $p;
}
return $ans;
}
echo PowerOFPINnfactorial(4, 2) . "\n";
?>
|
Javascript
<script>
function PowerOFPINnfactorial(n, p)
{
let ans = 0;
let temp = p;
while (temp <= n)
{
ans += n / temp;
temp = temp * p;
}
return ans;
}
document.write(PowerOFPINnfactorial(4, 2));
</script>
|
Kotlin
fun PowerOFPINnfactorial(n: Int, p: Int)
{
var ans = 0;
var temp = p;
while(temp<=n)
{
ans+=n/temp;
temp*=p;
}
println(ans)
}
fun main(args: Array<String>)
{
val n = 4
val p = 2
PowerOFPINnfactorial(n,p)
}
|
Output:
3
Time Complexity :O(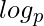 (n))
(n))
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...