Euler’s Four Square Identity
Last Updated :
05 May, 2021
According to Euler’s four square identity, the product of any two numbers a and b can be expressed as a sum of four squares if a and b both can individually be expressed as the sum of four squares.
Mathematically, if a = 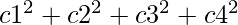 and b =
and b = 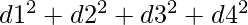
Then, a * b = 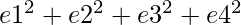
where c1, c2, c3, c4, d1, d2, d3, d4, e1, e2, e3, e4 are any integer.
Some examples are,
a = 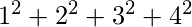 = 30
b =
= 30
b = 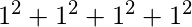 = 4
ab = a * b = 120 =
= 4
ab = a * b = 120 = 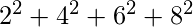 a =
a = 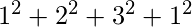 = 15
b =
= 15
b = 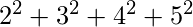 = 24
ab = a * b = 810 =
= 24
ab = a * b = 810 = 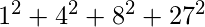 a =
a = 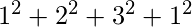 = 15
b =
= 15
b = 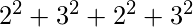 = 26
ab = a * b = 390 =
= 26
ab = a * b = 390 = 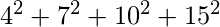
Example:
Input: a = 1 * 1 + 2 * 2 + 3 * 3 + 4 * 4
b = 1 * 1 + 1 * 1 + 1 * 1 + 1 * 1
Output: i = 0
j = 2
k = 4
l = 10
Product of 30 and 4 can be written as sum of squares of i, j, k, l
120 = 0 * 0 + 2 * 2 + 4 * 4 + 10 * 10
i = 2
j = 4
k = 6
l = 8
Product of 30 and 4 can be written as sum of squares of i, j, k, l
120 = 2 * 2 + 4 * 4 + 6 * 6 + 8 * 8
Explanation :
The product of the 2 numbers a(30) and b(4) can be represented as the sum of 4 squares as stated by Euler’s four square identity. The above are the 2 representations of the product a * b in the sum of 4 squares form. All possible representations of the product a*b in the sum of four squares form are shown.
Input: a = 1*1 + 2*2 + 3*3 + 1*1
b = 1*1 + 2*2 + 1*1 + 1*1
Output: i = 0
j = 1
k = 2
l = 10
Product of 15 and 7 can be written as sum of squares of i, j, k, l
105 = 0*0 + 1*1 + 2*2 + 10*10
i = 0
j = 4
k = 5
l = 8
Product of 15 and 7 can be written as sum of squares of i, j, k, l
105 = 0*0 + 4*4 + 5*5 + 8*8
i = 1
j = 2
k = 6
l = 8
Product of 15 and 7 can be written as sum of squares of i, j, k, l
105 = 1*1 + 2*2 + 6*6 + 8*8
i = 2
j = 2
k = 4
l = 9
Product of 15 and 7 can be written as sum of squares of i, j, k, l
105 = 2*2 + 2*2 + 4*4 + 9*9
i = 2
j = 4
k = 6
l = 7
Product of 15 and 7 can be written as sum of squares of i, j, k, l
105 = 2*2 + 4*4 + 6*6 + 7*7
i = 3
j = 4
k = 4
l = 8
Product of 15 and 7 can be written as sum of squares of i, j, k, l
105 = 3*3 + 4*4 + 4*4 + 8*8
Approach :
Brute Force :
A given number(a*b) can be represented in a sum of 4 squares form by using 4 loops i, j, k, l to find each of the four squares. This gives all possible combinations to form a*b as a sum of four squares. At each iteration of the innermost loop(l loop), check the sum with the product a*b. If there is a match, then print the 4 numbers(i, j, k, and l) whose sum of squares equals a*b.
C++
#include <bits/stdc++.h>
using namespace std;
#define show(x) cout << #x << " = " << x << "\n";
void check_euler_four_square_identity(int a, int b,
int ab)
{
int s = 0;
for (int i = 0;i * i <= ab;i ++)
{
s = i * i;
for (int j = i;j * j <= ab;j ++)
{
s = j * j + i * i;
for (int k = j;k * k <= ab;k ++)
{
s = k * k + j * j + i * i;
for (int l = k;l * l <= ab;l ++)
{
s = l * l + k * k + j * j + i * i;
if (s == ab)
{
show(i);
show(j);
show(k);
show(l);
cout <<""
<< "Product of " << a
<< " and " << b;
cout << " can be written"<<
" as sum of squares of i, "<<
"j, k, l\n";
cout << ab << " = ";
cout << i << "*" << i << " + ";
cout << j << "*" << j << " + ";
cout << k << "*" << k << " + ";
cout << l << "*" << l << "\n";
cout << "\n";
}
}
}
}
}
}
int main()
{
int a = 30;
int b = 4;
int ab = a * b;
check_euler_four_square_identity(a, b, ab);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static void check_euler_four_square_identity(int a,
int b,
int ab)
{
int s = 0;
for (int i = 0;
i * i <= ab; i ++)
{
s = i * i;
for (int j = i;
j * j <= ab; j ++)
{
s = j * j + i * i;
for (int k = j;
k * k <= ab; k ++)
{
s = k * k + j *
j + i * i;
for (int l = k;
l * l <= ab; l ++)
{
s = l * l + k * k +
j * j + i * i;
if (s == ab)
{
System.out.print("i = " +
i + "\n");
System.out.print("j = " +
j + "\n");
System.out.print("k = " +
k + "\n");
System.out.print("l = " +
l + "\n");
System.out.print("Product of " +
a + " and " + b);
System.out.print(" can be written"+
" as sum of squares of i, "+
"j, k, l\n");
System.out.print(ab + " = ");
System.out.print(i + "*" +
i + " + ");
System.out.print(j + "*" +
j + " + ");
System.out.print(k + "*" +
k + " + ");
System.out.print(l + "*" +
l + "\n");
System.out.println();
}
}
}
}
}
}
public static void main (String[] args)
{
int a = 30;
int b = 4;
int ab = a * b;
check_euler_four_square_identity(a, b, ab);
}
}
|
Python3
def check_euler_four_square_identity(a, b, ab):
s = 0;
i = 0;
while (i * i <= ab):
s = i * i;
j = i;
while (j * j <= ab):
s = j * j + i * i;
k = j;
while (k * k <= ab):
s = k * k + j * j + i * i;
l = k;
while (l * l <= ab):
s = l * l + k * k + j * j + i * i;
if (s == ab):
print("i =", i);
print("j =", j);
print("k =", k);
print("l =", l);
print("Product of ", a,
"and", b, end = "");
print(" can be written as sum of",
"squares of i, j, k, l");
print(ab, "= ", end = "");
print(i, "*", i, "+ ", end = "");
print(j, "*", j, "+ ", end = "");
print(k, "*", k, "+ ", end = "");
print(l, "*", l);
print("");
l += 1;
k += 1;
j += 1;
i += 1;
a = 30;
b = 4;
ab = a * b;
check_euler_four_square_identity(a, b, ab);
|
C#
using System;
class GFG
{
static void check_euler_four_square_identity(int a,
int b,
int ab)
{
int s = 0;
for (int i = 0; i * i <= ab; i ++)
{
s = i * i;
for (int j = i; j * j <= ab; j ++)
{
s = j * j + i * i;
for (int k = j; k * k <= ab; k ++)
{
s = k * k + j *
j + i * i;
for (int l = k; l * l <= ab; l ++)
{
s = l * l + k * k +
j * j + i * i;
if (s == ab)
{
Console.Write("i = " + i + "\n");
Console.Write("j = " + j + "\n");
Console.Write("k = " + k + "\n");
Console.Write("l = " + l + "\n");
Console.Write("Product of " + a +
" and " + b);
Console.Write(" can be written"+
" as sum of squares of i, "+
"j, k, l\n");
Console.Write(ab + " = ");
Console.Write(i + "*" + i + " + ");
Console.Write(j + "*" + j + " + ");
Console.Write(k + "*" + k + " + ");
Console.Write(l + "*" + l + "\n");
Console.Write("\n");
}
}
}
}
}
}
static void Main()
{
int a = 30;
int b = 4;
int ab = a * b;
check_euler_four_square_identity(a, b, ab);
}
}
|
PHP
<?php
function check_euler_four_square_identity($a, $b, $ab)
{
$s = 0;
for ($i = 0; $i * $i <= $ab; $i ++)
{
$s = $i * $i;
for ($j = $i; $j * $j <= $ab; $j ++)
{
$s = $j * $j + $i * $i;
for ($k = $j; $k * $k <= $ab; $k ++)
{
$s = $k * $k + $j * $j + $i * $i;
for ($l = $k; $l * $l <= $ab; $l ++)
{
$s = $l * $l + $k * $k +
$j * $j + $i * $i;
if ($s == $ab)
{
echo("i = " . $i . "\n");
echo("j = " . $j . "\n");
echo("k = " . $k . "\n");
echo("l = " . $l . "\n");
echo "". "Product of " .
$a . " and " . $b;
echo " can be written".
" as sum of squares of i, " .
"j, k, l\n";
echo $ab . " = ";
echo $i . "*" . $i. " + ";
echo $j . "*" . $j . " + ";
echo $k . "*" . $k . " + ";
echo $l . "*" . $l . "\n";
echo "\n";
}
}
}
}
}
}
$a = 30;
$b = 4;
$ab = $a * $b;
check_euler_four_square_identity($a, $b, $ab);
?>
|
Javascript
<script>
function check_euler_four_square_identity(a, b, ab)
{
let s = 0;
for (let i = 0; i * i <= ab; i ++)
{
s = i * i;
for (let j = i; j * j <= ab; j ++)
{
s = j * j + i * i;
for (let k = j; k * k <= ab; k ++)
{
s = k * k + j *
j + i * i;
for (let l = k; l * l <= ab; l ++)
{
s = l * l + k * k +
j * j + i * i;
if (s == ab)
{
document.write("i = " + i +
"</br>");
document.write("j = " + j +
"</br>");
document.write("k = " + k +
"</br>");
document.write("l = " + l +
"</br>");
document.write("Product of " + a +
" and " + b);
document.write(" can be written"+
" as sum of squares of i, "+
"j, k, l" +
"</br>");
document.write(ab + " = ");
document.write(i + "*" + i +
" + ");
document.write(j + "*" + j +
" + ");
document.write(k + "*" + k +
" + ");
document.write(l + "*" + l +
"</br>");
document.write("</br>");
}
}
}
}
}
}
let a = 30;
let b = 4;
let ab = a * b;
check_euler_four_square_identity(a, b, ab);
</script>
|
Output: i = 0
j = 2
k = 4
l = 10
Product of 30 and 4 can be written as sum of squares of i, j, k, l
120 = 0*0 + 2*2 + 4*4 + 10*10
i = 2
j = 4
k = 6
l = 8
Product of 30 and 4 can be written as sum of squares of i, j, k, l
120 = 2*2 + 4*4 + 6*6 + 8*8
Improved Algorithm:
The time complexity of the above algorithm is 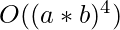 in the worst case. This can be reduced to
in the worst case. This can be reduced to 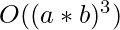 by subtracting the squares of i, j, and k from the product a*b for all (i, j, k) and checking if that value is a perfect square or not. If it is a perfect square, then we have found the solution.
by subtracting the squares of i, j, and k from the product a*b for all (i, j, k) and checking if that value is a perfect square or not. If it is a perfect square, then we have found the solution.
C++
#include<bits/stdc++.h>
using namespace std;
void checkEulerFourSquareIdentity(int a, int b)
{
int ab = a * b;
bool flag = false;
int i = 0;
while(i * i <= ab)
{
int j = i;
while (i * i + j * j <= ab)
{
int k = j;
while(i * i + j * j +
k * k <= ab)
{
double l = sqrt(ab - (i * i + j *
j + k * k));
if (floor(l) == ceil(l) && l >= k)
{
flag = true;
cout<<"i = " << i << "\n";
cout<<"j = " << j << "\n";
cout<<"k = " << k << "\n";
cout<<"l = " << (int)l << "\n";
cout<<"Product of " << a << " and "<< b <<
" can be written as sum of squares"<<
" of i, j, k, l \n";
cout<<ab + " = " << i << "*" << i << " + " <<
j << "*" << j<< " + " << k << "*" <<
k << " + " << (int)l << "*" <<
(int)l << "\n";
}
k += 1;
}
j += 1;
}
i += 1;
}
if (flag == false)
{
cout<< "Solution doesn't exist!\n";
return ;
}
}
int main()
{
int a = 30;
int b = 4;
checkEulerFourSquareIdentity(a, b);
return 0;
}
|
Java
class GFG
{
public static void checkEulerFourSquareIdentity(int a,
int b)
{
int ab = a * b;
boolean flag = false;
int i = 0;
while(i * i <= ab)
{
int j = i;
while (i * i + j * j <= ab)
{
int k = j;
while(i * i + j * j +
k * k <= ab)
{
double l = Math.sqrt(ab - (i * i + j *
j + k * k));
if (Math.floor(l) == Math.ceil(l) && l >= k)
{
flag = true;
System.out.print("i = " + i + "\n");
System.out.print("j = " + j + "\n");
System.out.print("k = " + k + "\n");
System.out.print("l = " + (int)l + "\n");
System.out.print("Product of " + a + " and "+ b +
" can be written as sum of squares"+
" of i, j, k, l \n");
System.out.print(ab + " = " + i + "*" + i + " + " +
j + "*" + j + " + " + k + "*" +
k + " + " + (int)l + "*" +
(int)l + "\n");
}
k += 1;
}
j += 1;
}
i += 1;
}
if (flag == false)
{
System.out.println("Solution doesn't exist!");
return ;
}
}
public static void main(String[] args)
{
int a = 30;
int b = 4;
checkEulerFourSquareIdentity(a, b);
}
}
|
Python3
def checkEulerFourSquareIdentity(a, b):
ab = a*b
flag = False
i = 0
while i*i <= ab:
j = i
while i*i + j*j <= ab:
k = j
while i*i + j*j + k*k <= ab:
l = (ab - (i*i + j*j + k*k))**(0.5)
if l == int(l) and l >= k:
flag = True
print("i = ",i)
print("j = ",j)
print("k = ",k)
print("l = ",l)
print("Product of", a , "and" , b ,
"can be written as sum of squares of i, j, k, l" )
print(ab," = ",i,"*",i,"+",j,"*",j,"+",
k,"*",k,"+",l,"*",l)
k += 1
j += 1
i += 1
if flag == False:
print("Solution doesn't exist!")
return
a, b = 30, 4
checkEulerFourSquareIdentity(a,b)
|
C#
using System;
class GFG
{
public static void checkEulerFourSquareIdentity(int a,
int b)
{
int ab = a * b;
bool flag = false;
int i = 0;
while(i * i <= ab)
{
int j = i;
while (i * i + j * j <= ab)
{
int k = j;
while(i * i + j * j +
k * k <= ab)
{
double l = Math.Sqrt(ab - (i * i + j *
j + k * k));
if (Math.Floor(l) == Math.Ceiling(l) && l >= k)
{
flag = true;
Console.Write("i = " + i + "\n");
Console.Write("j = " + j + "\n");
Console.Write("k = " + k + "\n");
Console.Write("l = " + (int)l + "\n");
Console.Write("Product of " + a + " and "+ b +
" can be written as sum of squares"+
" of i, j, k, l \n");
Console.Write(ab + " = " + i + "*" + i + " + " +
j + "*" + j + " + " + k + "*" +
k + " + " + (int)l + "*" +
(int)l + "\n");
}
k += 1;
}
j += 1;
}
i += 1;
}
if (flag == false)
{
Console.WriteLine("Solution doesn't exist!");
return ;
}
}
public static void Main()
{
int a = 30;
int b = 4;
checkEulerFourSquareIdentity(a, b);
}
}
|
PHP
<?php
function checkEulerFourSquareIdentity($a, $b)
{
$ab = $a * $b;
$flag = false;
$i = 0;
while($i * $i <= $ab)
{
$j = $i;
while ($i * $i + $j * $j <= $ab)
{
$k = $j;
while($i * $i + $j * $j +
$k * $k <= $ab)
{
$l = sqrt($ab - ($i * $i + $j *
$j + $k * $k));
if (floor($l) == ceil($l) && $l >= $k)
{
$flag = true;
print("i = " . $i . "\n");
print("j = " . $j . "\n");
print("k = " . $k . "\n");
print("l = " . $l . "\n");
print("Product of " . $a . " and " . $b .
" can be written as sum of squares" .
" of i, j, k, l \n");
print($ab . " = " . $i . "*" . $i . " + " .
$j . "*" . $j . " + " . $k . "*" .
$k . " + " . $l . "*" . $l . "\n");
}
$k += 1;
}
$j += 1;
}
$i += 1;
}
if ($flag == false)
{
print("Solution doesn't exist!");
return 0;
}
}
$a = 30;
$b = 4;
checkEulerFourSquareIdentity($a, $b);
?>
|
Javascript
<script>
function checkEulerFourSquareIdentity(a, b)
{
let ab = a * b;
let flag = false;
let i = 0;
while(i * i <= ab)
{
let j = i;
while (i * i + j * j <= ab)
{
let k = j;
while(i * i + j * j +
k * k <= ab)
{
let l = Math.sqrt(ab - (i * i + j * j + k * k));
if (Math.floor(l) == Math.ceil(l) && l >= k)
{
flag = true;
document.write("i = " + i + "</br>");
document.write("j = " + j + "</br>");
document.write("k = " + k + "</br>");
document.write("l = " + l + "</br>");
document.write("Product of " + a + " and "+ b +
" can be written as sum of squares"+
" of i, j, k, l " + "</br>");
document.write(ab + " = " + i + "*" + i + " + " +
j + "*" + j + " + " + k + "*" +
k + " + " + l + "*" +
l + "</br>");
}
k += 1;
}
j += 1;
}
i += 1;
}
if (flag == false)
{
document.write("Solution doesn't exist!" + "</br>");
return;
}
}
let a = 30;
let b = 4;
checkEulerFourSquareIdentity(a, b);
</script>
|
Output:
i = 0
j = 2
k = 4
l = 10
Product of 30 and 4 can be written as sum of squares of i, j, k, l
120 = 0*0 + 2*2 + 4*4 + 10*10
i = 2
j = 4
k = 6
l = 8
Product of 30 and 4 can be written as sum of squares of i, j, k, l
120 = 2*2 + 4*4 + 6*6 + 8*8
Share your thoughts in the comments
Please Login to comment...