Lagrange’s four square theorem
Last Updated :
23 Aug, 2022
Lagrange’s Four Square Theorem states that every natural number can be written as sum of squares of four non negative integers.
For eg. 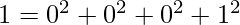
Similarly 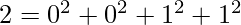
Similarly for any
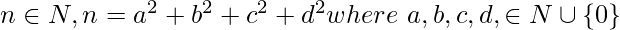
The above identity may be derived from Euler’s four square identity: which says we can write a product of 2 numbers (which can be written as sum of 4 squares) as the sum of 4 squares.
C++
#include <bits/stdc++.h>
using namespace std;
void printFourSquares(int a)
{
for (int i = 0; i * i <= a; i++) {
for (int j = i; j * j <= a; j++) {
for (int k = j; k * k <= a; k++) {
for (int l = k; l * l <= a; l++) {
if (i * i + j * j + k * k + l * l == a) {
cout << a << " = " << i << "*" << i
<< " + " << j << "*" << j << " + ";
cout << k << "*" << k << " + "
<< l << "*" << l << "\n";
}
}
}
}
}
}
int main()
{
int a = 74;
printFourSquares(a);
return 0;
}
|
Java
class GFG
{
static void printFourSquares(int a)
{
for (int i = 0; i * i <= a; i++)
{
for (int j = i; j * j <= a; j++)
{
for (int k = j; k * k <= a; k++)
{
for (int l = k; l * l <= a; l++)
{
if (i * i + j * j + k * k + l * l == a)
{
System.out.print( a + " = " + i + "*" + i
+ " + " + j + "*" + j + " + ");
System.out.println( k + "*" + k + " + "
+ l + "*" + l);
}
}
}
}
}
}
public static void main(String[] args)
{
int a = 74;
printFourSquares(a);
}
}
|
Python3
def printFourSquares(a) :
i = 0
while (i * i <= a) :
j = i
while (j * j <= a) :
k = j
while (k * k <= a) :
l = k
while (l * l <= a) :
if (i * i + j * j + k * k + l * l == a) :
print ("{} = {}*{} + {}*{} +".
format(a,i,i,j,j), end = " ")
print ("{}*{} + {}*{}".
format(k,k,l,l), end="\n")
l = l + 1
k = k + 1
j = j + 1
i = i + 1
a = 74
printFourSquares(a)
|
C#
using System;
class GFG
{
static void printFourSquares(int a)
{
for (int i = 0; i * i <= a; i++)
{
for (int j = i; j * j <= a; j++)
{
for (int k = j; k * k <= a; k++) {
for (int l = k; l * l <= a; l++)
{
if (i * i + j * j + k * k + l * l == a)
{
Console.Write( a + " = " + i + "*" + i + " + "
+ j + "*" + j + " + ");
Console.Write( k + "*" + k + " + "
+ l + "*" + l + "\n");
}
}
}
}
}
}
public static void Main()
{
int a = 74;
printFourSquares(a);
}
}
|
PHP
<?php
function printFourSquares($a)
{
for ($i = 0; $i * $i <= $a; $i++) {
for ( $j = $i; $j * $j <= $a; $j++) {
for ($k = $j; $k * $k <= $a; $k++) {
for ($l = $k; $l * $l <= $a; $l++) {
if ($i * $i + $j * $j + $k * $k
+ $l * $l == $a)
{
echo $a , " = " , $i , "*" ,$i,
" + " , $j , "*" , $j , " + ";
echo $k , "*" , $k , " + ",
$l , "*" , $l , "\n";
}
}
}
}
}
}
$a = 74;
printFourSquares($a);
?>
|
Javascript
<script>
function printFourSquares(a)
{
for(let i = 0; i * i <= a; i++)
{
for(let j = i; j * j <= a; j++)
{
for(let k = j; k * k <= a; k++)
{
for(let l = k; l * l <= a; l++)
{
if (i * i + j * j + k * k + l * l == a)
{
document.write(a + " = " + i + "*" +
i + " + " + j + "*" +
j + " + ");
document.write(k + "*" + k + " + " +
l + "*" + l + "</br>");
}
}
}
}
}
}
let a = 74;
printFourSquares(a);
</script>
|
Output: 74 = 0*0 + 0*0 + 5*5 + 7*7
74 = 0*0 + 1*1 + 3*3 + 8*8
74 = 0*0 + 3*3 + 4*4 + 7*7
74 = 1*1 + 1*1 + 6*6 + 6*6
74 = 2*2 + 3*3 + 5*5 + 6*6
Time complexity : O(a2)
Auxiliary Space : O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...