Lucas Primality Test

Difficulty Level : Medium
Last Updated : 26 Oct, 2020

A number p greater than one is prime if and only if the only divisors of p are 1 and p. First few prime numbers are 2, 3, 5, 7, 11, 13, …
The Lucas test is a primality test for a natural number n, it can test primality of any kind of number.
It follows from Fermat’s Little Theorem: If p is prime and a is an integer, then a^p is congruent to a (mod p )

Lucas’ Test : A positive number n
is prime if there exists an integer a (1 < a < n) such that :

$a^{{n-1}}\ \equiv \ 1{\pmod n}$

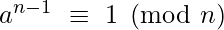
And for every prime factor q of (n-1),

$a^{{({n-1})/q}}\ \not \equiv \ 1{\pmod n}$

Examples :

Input :  n = 7
Output : 7 is Prime
Explanation : let's take a = 3, 
then 3^6 % 7 = 729 % 7 = 1 (1st 
condition satisfied). Prime factors 
of 6 are 2 and 3,
3^(6/2) % 7 = 3^3 % 7 = 27 % 7 = 6
3^(6/3) % 7 = 3^2 % 7 = 9 % 7 = 2
Hence, 7 is Prime  

Input :  n = 9
Output : 9 is composite
Explanation : Let's take a = 2,
then 2^8 % 9 = 256 % 9 = 4
Hence 9 is composite

lucasTest(n):
If n is even
    return composite
Else
   Find all prime factors of n-1
   for i=2 to n-1
      pick 'a' randomly in range [2, n-1]
      if a^(n-1) % n not equal 1:
          return composite
      else 
          // for all q, prime factors of (n-1)
          if a^(n-1)/q % n not equal 1 
             return prime
   Return probably prime

Problems Associated with Lucas’s test are :

Knowing all of the prime factors of n-1
Finding an appropriate choice for a

C++

// C++ Program for Lucas Primality Test 
#include <bits/stdc++.h> 
using namespace std; 
 
// function to generate prime factors of n 
void primeFactors(int n, vector<int>& factors) 
{ 
    // if 2 is a factor 
    if (n % 2 == 0) 
        factors.push_back(2); 
    while (n % 2 == 0) 
        n = n / 2; 
         
    // if prime > 2 is factor 
    for (int i = 3; i <= sqrt(n); i += 2) { 
        if (n % i == 0) 
            factors.push_back(i); 
        while (n % i == 0) 
            n = n / i; 
    } 
    if (n > 2) 
    factors.push_back(n); 
} 
 
// this function produces power modulo 
// some number. It can be optimized to 
// using 
int power(int n, int r, int q) 
{ 
    int total = n; 
    for (int i = 1; i < r; i++) 
        total = (total * n) % q; 
    return total; 
} 
 
string lucasTest(int n) 
{ 
    // Base cases 
    if (n == 1) 
        return "neither prime nor composite"; 
    if (n == 2) 
        return "prime"; 
    if (n % 2 == 0) 
        return "composite1"; 
         
         
    // Generating and storing factors 
    // of n-1 
    vector<int> factors; 
    primeFactors(n - 1, factors); 
 
    // Array for random generator. This array 
    // is to ensure one number is generated 
    // only once 
    int random[n - 3]; 
    for (int i = 0; i < n - 2; i++) 
        random[i] = i + 2; 
         
    // shuffle random array to produce randomness 
    shuffle(random, random + n - 3, 
            default_random_engine(time(0))); 
 
    // Now one by one perform Lucas Primality 
    // Test on random numbers generated. 
    for (int i = 0; i < n - 2; i++) { 
        int a = random[i]; 
        if (power(a, n - 1, n) != 1) 
            return "composite"; 
 
        // this is to check if every factor 
        // of n-1 satisfy the condition 
        bool flag = true; 
        for (int k = 0; k < factors.size(); k++) { 
            // if a^((n-1)/q) equal 1 
            if (power(a, (n - 1) / factors[k], n) == 1) { 
                flag = false; 
                break; 
            } 
        } 
 
        // if all condition satisfy 
        if (flag) 
            return "prime"; 
    } 
    return "probably composite"; 
} 
 
// Driver code 
int main() 
{ 
    cout << 7 << " is " << lucasTest(7) << endl; 
    cout << 9 << " is " << lucasTest(9) << endl; 
    cout << 37 << " is " << lucasTest(37) << endl; 
    return 0; 
} 

Python3

# Python3 program for Lucas Primality Test
import random
import math
 
# Function to generate prime factors of n
def primeFactors(n, factors):
     
    # If 2 is a factor
    if (n % 2 == 0):
        factors.append(2)
         
    while (n % 2 == 0):
        n = n // 2
         
    # If prime > 2 is factor
    for i in range(3, int(math.sqrt(n)) + 1, 2):
        if (n % i == 0):
            factors.append(i)
             
        while (n % i == 0):
            n = n // i
             
    if (n > 2):
        factors.append(n)
         
    return factors
     
# This function produces power modulo 
# some number. It can be optimized to 
# using 
def power(n, r, q):
     
    total = n
     
    for i in range(1, r):
        total = (total * n) % q
         
    return total
  
def lucasTest(n):
  
    # Base cases 
    if (n == 1):
        return "neither prime nor composite"
    if (n == 2):
        return "prime"
    if (n % 2 == 0):
        return "composite1"
          
    # Generating and storing factors 
    # of n-1
    factors = []
     
    factors = primeFactors(n - 1, factors)
  
    # Array for random generator. This array 
    # is to ensure one number is generated 
    # only once
    rand = [i + 2 for i in range(n - 3)]
          
    # Shuffle random array to produce randomness
    random.shuffle(rand)
  
    # Now one by one perform Lucas Primality
    # Test on random numbers generated.
    for i in range(n - 2):
        a = rand[i] 
         
        if (power(a, n - 1, n) != 1):
            return "composite"
  
        # This is to check if every factor 
        # of n-1 satisfy the condition
        flag = True
         
        for k in range(len(factors)):
             
            # If a^((n-1)/q) equal 1
            if (power(a, (n - 1) // factors[k], n) == 1):
                flag = False
                break
  
        # If all condition satisfy
        if (flag):
            return "prime"
     
    return "probably composite"
     
# Driver code 
if __name__=="__main__":
     
    print(str(7) + " is " + lucasTest(7))
    print(str(9) + " is " + lucasTest(9))
    print(str(37) + " is " + lucasTest(37))
 
# This code is contributed by rutvik_56

Output:

7 is prime
9 is composite
37 is prime

This method is quite complicated and inefficient as compared to other primality tests. And the main problems are factors of ‘n-1’ and choosing appropriate ‘a’.

Other Primality tests:

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.

My Personal Notes

Related Articles

C++

Python3