Vantieghems Theorem for Primality Test

Difficulty Level : Medium
Last Updated : 13 May, 2021

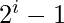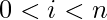Vantieghems Theorem is a necessary and sufficient condition for a number to be prime. It states that for a natural number n to be prime, the product of $2^i - 1$ where $0 < i < n$ , is congruent to $n~(mod~(2^n - 1))$ .
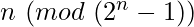In other words, a number n is prime if and only if.
$\prod _{1\leq i\leq n-1}\left(2^{i}-1\right)\equiv n\mod \left(2^{n}-1\right).$
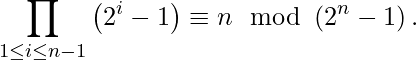
Examples:

For n = 3, final product is (2¹ – 1) * (2² – 1) = 1*3 = 3. 3 is congruent to 3 mod 7. We get 3 mod 7 from expression 3 * (mod (2³ – 1)), therefore 3 is prime.
For n = 5, final product is 1*3*7*15 = 315. 315 is congruent to 5(mod 31), therefore 5 is prime.
For n = 7, final product is 1*3*7*15*31*63 = 615195. 615195 is congruent to 7(mod 127), therefore 7 is prime.
For n = 4, final product 1*3*7 = 21. 21 is not congruent to 4(mod 15), therefore 4 is composite.

Another way to state above theorem is, if 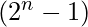$(2^n - 1)$ divides 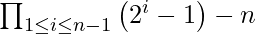$\prod _{1\leq i\leq n-1}\left(2^{i}-1\right) - n$ , then n is prime.

C++

// C++ code to verify Vantieghem's Theorem
#include <bits/stdc++.h>
using namespace std;
 
void checkVantieghemsTheorem(int limit)
{
    long long unsigned prod = 1;
    for (long long unsigned n = 2; n < limit; n++) {
 
        // Check if above condition is satisfied
        if (((prod - n) % ((1LL << n) - 1)) == 0)
            cout << n << " is prime\n";
 
        // product of previous powers of 2
        prod *= ((1LL << n) - 1);
    }
}
 
// Driver code
int main()
{
    checkVantieghemsTheorem(10);
    return 0;
}

Java

// Java code to verify Vantieghem's Theorem
import java.util.*;
class GFG
{
 
static void checkVantieghemsTheorem(int limit)
{
    long prod = 1;
    for (long n = 2; n < limit; n++)
    {
 
        // Check if above condition is satisfied
        if (((prod - n < 0 ? 0 : prod - n) % ((1 << n) - 1)) == 0)
            System.out.print(n + " is prime\n");
 
        // product of previous powers of 2
        prod *= ((1 << n) - 1);
    }
}
 
// Driver code
public static void main(String []args)
{
    checkVantieghemsTheorem(10);
}
}
 
// This code is contributed by rutvik_56.

Python3

# Python3 code to verify Vantieghem's Theorem
def checkVantieghemsTheorem(limit):
     
    prod = 1
    for n in range(2, limit):
         
        # Check if above condition is satisfied
        if n == 2:
            print(2, "is prime")
        if (((prod - n) % ((1 << n) - 1)) == 0):
            print(n, "is prime")
             
        # Product of previous powers of 2
        prod *= ((1 << n) - 1)
     
# Driver code
checkVantieghemsTheorem(10)
 
# This code is contributed by shubhamsingh10

C#

// C# code to verify Vantieghem's Theorem
using System;
class GFG
{
  static void checkVantieghemsTheorem(int limit)
  {
    long prod = 1;
    for (long n = 2; n < limit; n++)
    {
 
      // Check if above condition is satisfied
      if (((prod - n < 0 ? 0 : prod - n) % ((1 << (int)n) - 1)) == 0)
        Console.Write(n + " is prime\n");
 
      // product of previous powers of 2
      prod *= ((1 << (int)n) - 1);
    }
  }
 
  // Driver code
  public static void Main()
  {
    checkVantieghemsTheorem(10);
  }
}
 
// This code is contributed by pratham76.

Javascript

<script>
 
// Javascript code to verify Vantieghem's Theorem
 
function checkVantieghemsTheorem( limit)
{
    let prod = 1;
    for (let n = 2; n < limit; n++) {
 
        // Check if above condition is satisfied
        if (n == 2)
            document.write(2 + " is prime" + "</br>");
        if (((prod - n) % ((1 << n) - 1)) == 0)
            document.write( n + " is prime" + "</br>");
 
        // product of previous powers of 2
        prod *= ((1 << n) - 1);
    }
}
 
// Driver Code
checkVantieghemsTheorem(10);
 
// This code is contributed by jana_sayantan.
</script>

Output:

2 is prime
3 is prime
5 is prime
7 is prime

The above code does not work for values of n higher than 11. It causes overflow in prod evaluation.

My Personal Notes

Related Articles

Related Articles

Vantieghems Theorem for Primality Test

C++

Java

Python3

C#

Javascript