Pythagorean Identities

Pythagorean Identities in trigonometry are derived from Pythagorean Theorem. They are also called Pythagorean Trigonometric Identities. The basic Pythagorean identity is sin²θ + cos²θ is equal to 1.

Learn about, Pythagorean identities in trigonometry, list of Pythagorean identities their proof and others in detail in this article.

What are Pythagorean Identities?

Pythagorean identities are important identities in trigonometry that are based on the Pythagoras theorem. It relates the square of one trigonometric ratio with the other. It can be used to solve complex trigonometric problems easily and also used to prove various other trigonometric identities.

Pythagorean Trig Identities

Pythagorean identities are the identities which gives us the relation between the square of one trigonometric ratio to square of another trigonometric ratio.

These identities are called Pythagorean identities because they follow Pythagoras theorem. In trigonometry, we have three basic Pythagorean identities which are:

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

Pythagoras Theorem

Pythagoras theorem states that in a right-angled triangle, the square of hypotenuse is equal to the sum of squares of perpendicular and base. The formula for Pythagoras theorem is given by:

(Hypotenuse)² = (Perpendicular)² + (Base)²

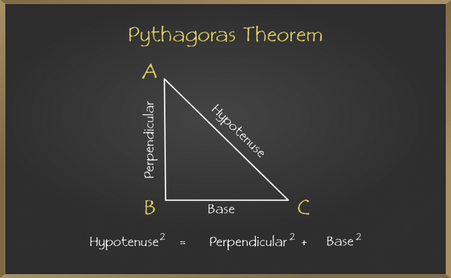
In the above figure is of right-angled triangle ABC with perpendicular AB, base BC and hypotenuse AC. So, by the Pythagoras theorem: AC² = AB² + BC²

List of Pythagorean Identities

As we know the three basic Pythagorean identities in trigonometry are:

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

However, from these identities we can derive the other six identities as well, which are given by:

• sin²θ + cos²θ = 1
  • 1 – cos²θ = sin²θ
  • 1 – sin²θ = cos²θ
• 1 + tan²θ = sec²θ
  • sec²θ – tan²θ = 1
  • tan²θ = sec²θ – 1
• 1 + cot²θ = cosec²θ
  • cosec²θ – cot²θ = 1
  • cot²θ = cosec²θ – 1

Pythagorean Identities Derivation

Pythagorean identites can be easily proved by applying Pythagorean thorem in a right angle triangle. This is proved below:

Pythagorean Identity for Sin and Cos

Pythagorean identity for sine and cosine states that the sum of squares of sine and cosine is equal to 1. Pythagorean identity for sine and cosine is given by:

sin²θ + cos²θ = 1

Derivation of sin²θ + cos²θ = 1

Consider a right-angled triangle ABC with perpendicular AB, base BC and hypotenuse AC.

By the Pythagoras theorem

AC² = AB² + BC²

Dividing both side by AC²

[AC² / AC²] = [AB² / AC²] + [BC² / AC²]

⇒ 1 = [AB / AC]² + [BC / AC]² . . . (a)

From the above triangle

[AB / AC] = sinθ

[BC / AC] = cosθ

Putting these values in equation a, we get

1 = sin²θ + cos²θ, or

⇒ sin²θ + cos²θ = 1

Hence Proved.

Pythagorean Identity for Tan and Sec

Pythagorean identity for tan and sec is given by:

sec²θ – tan²θ = 1

or

1 + tan²θ = sec²θ

Derivation of 1 + tan²θ = sec²θ

Consider a right-angled triangle ABC with perpendicular AB, base BC and hypotenuse AC.

By the Pythagoras theorem

AC² = AB² + BC²

Dividing both side by BC²

[AC² / BC²] = [AB² / BC²] + [BC² / BC²]

⇒ AC / BC]² = [AB / BC]² + 1 . . . (b)

From the above triangle, we have

[AC / BC] = sec θ

[AB / BC] = tan θ

Putting these values in equation b, we get

sec²θ = tan²θ + 1, or

sec²θ – tan²θ = 1

Hence Proved

Pythagorean Identity for Cot and Cosec

Pythagorean identity for cot and cosec is given by:

1 + cot²θ = cosec²θ

Derivation of 1 + cot²θ = cosec²θ

Consider a right-angled triangle ABC with perpendicular AB, base BC and hypotenuse AC.

By the Pythagoras theorem, we have

AC² = AB² + BC²

Dividing both side by AB², we get

[AC² / AB²] = [AB² / AB²] + [BC² / AB²]

⇒ [AC / AB]² = 1 + [BC / AB]² . . . (c)

From the above triangle, we know

[AC / AB] = cosec θ

[BC/ AB] = cot θ

Putting these values in equation c we get,

cosec²θ = 1 + cot²θ, or

cosec²θ – cot²θ = 1

Hence Proved

Applications of Pythagorean Identities

Some applications of Pythagorean identities in trigonometry are:

• Pythagorean identities can be used to derive other trigonometric identities.
• It can also be used in calculation of heights and distances.
• It can be used to simplify trigonometric problems.

Conclusion(Pythagorean Trigonometric Identities)

From the above discussion we can conclude that we have three main Pythagorean identities in trigonometry. The three Pythagorean identities are

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

These Pythagorean identities are proved using Pythagoras theorem. The Pythagoras theorem says that in a right-angled triangle the square of the longest side is equal to the sum of squares of other two sides. The Pythagorean identities are useful in the derivation and simplification of other trigonometric identities and problems.

Read More,

• Trigonometry
• Trigonometric Formulas
• Pythagorean Triples

Pythagorean Identities Examples

Example 1: If the angle y is in second quadrant and cos y = 5/13. Find the value of sin y.

Solution:

By Pythagorean identity

sin²y + cos²y = 1

⇒ sin²y + (5/13)²= 1

⇒ sin²y = 1 – (25/169)

⇒ sin²y = 144 / 169

⇒ sin y = ± 12/13

Since, sin is positive in second quadrant so we will take positive value i.e., sin y = 12/13.

Example 2: Evaluate [1/ (1 – cos x)] + [1/ (1 + cos x)]

Solution:

Given,

• [1/ (1 – cos x)] + [1/ (1 + cos x)]

= [(1 + cosx) + (1 – cos x)] / [(1 + cosx) (1 – cos x)]

= 2 / (1²– cos²x)

= 2 / (1 – cos²x)

By Pythagorean identity, sin²y + cos²y = 1 or sin²y = 1 – cos²y

⇒ [1/ (1 – cos x)] + [1/ (1 + cos x)] = 2 / sin²x

⇒ [1/ (1 – cos x)] + [1/ (1 + cos x)] = 2 cosec²x

Example 3: Simplify (tanθ + secθ)(tanθ – secθ)

Solution:

Given,

• (tan θ + sec θ)(tan θ – sec θ)

= (tan² θ – sec² θ) [ As (a-b)(a+b) = a² – b²]

By Pythagorean identity, we have

sec² θ – tan² θ = 1

(tan θ + sec θ)(tan θ – sec θ) = -(sec² θ – tan² θ) = -1

Hence, (tan θ + sec θ)(tan θ – sec θ) = -1

Example 4: Evaluate (cosec z + cot z) [(1 – cos z)/sin z]

Solution:

Given,

• (cosec z + cot z) [(1 – cos z)/sin z]

Simplifying,

(cosec z + cot z) [(1/sin z) – (cos z/sin z)]

= (cosec z + cot z) (cosec z – cot z) [As 1/ sin z = cosec z and cos z/sinz = cot z]

= (cosec²z – cot²z) [ As (a-b)(a+b) = a² – b²]

By Pythagorean Identity we have, cosec²θ – cot²θ = 1

Hence, (cosec z + cot z) [(1 – cos z)/sin z] = 1

Practice Questions on Pythagorean Identities

Q1: If cot A = 4/3 then, find the value of cosec A.

Q2: Evaluate [1/ (1 – cosec x)] [1/ (1 + cosec x)].

Q3: Simplify (cosecθ + cotθ)(cosecθ – cotθ).

Q4: Prove that: sin⁴x – cos⁴x = sin²x – cos²x.

FAQs on Pythagorean Identities

What are Pythagorean Identities?

The identities in trigonometry that are based on Pythagoras theorem are called as Pythagorean Identities.

What is Pythagoras Theorem?

Pythagoras theorem states that in a right-angled triangle the square of hypotenuse is equal to the sum of squares of other two sides.

What are the 3 Pythagorean Identities?

3 Pythagorean Identities are:

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

How to Prove Pythagorean Identities in Trigonometry?

To prove Pythagorean identities in trigonometry we use Pythagoras theorem.

What is Pythagorean Triple Rule?

Pythagorean triple rule is in a right-angled triangle (hypotenuse)² = (Perpendicular)² + (Base)².

What are two Quotient Identities?

The 2 quotient identities are:

• tan θ = sin θ/cos θ
• cot θ = cos θ/sin θ

List all Pythagorean Identities.

All 9 Pythagorean identities are:

Pythagorean Identity	Alternative Identites
sin2θ + cos2θ = 1	1 – sin2θ = cos2 θ OR 1 – cos2θ = sin2θ
sec2θ – tan2θ = 1	1 + tan2θ = sec2θ OR sec2θ – 1 = tan2θ
cosec2θ – cot2θ = 1	1 + cot2θ = cosec2θ OR cosec2θ – 1 = cot2θ