Differentiation of Trigonometric Functions

Differentiation of Trigonometric Functions as the name suggests discusses the various differentiation of Trigonometric Functions such as sin, cos, tan, cot, sec, and cosec. Differentiation is an important part of the calculus and is defined as the rate of change of one quantity with respect to some other quantity. The differentiation of the trigonometric functions is used in real life in various fields like computers, electronics, and mathematics.

In this article, we will learn about the differentiation of trigonometric functions along with the formulas, their related proofs, and their applications. Also, we will solve some examples and get answers to some FAQs on the differentiation of trigonometric functions. Let’s start our learning on the topic of Differentiation of Trigonometric functions.

What is Differentiation?

The differentiation of a function is the rate of change of a function with respect to any variable. The derivative of f(x) is denoted as f'(x) or (d /dx)[f(x)].

The procedure of differentiating the trigonometric functions is called the differentiation of trigonometric functions. In other words, finding the rate of change of trigonometric functions with respect to the angles is called trigonometric function differentiation.

The six basic trigonometric functions are sin, cos, tan, cosec, sec, and cot. We will find the derivatives of all the trigonometric functions with their formulas and proof.

Differentiation Rule For Trigonometric Functions

The differentiation of six basic trigonometric functions are as follows:

Function	Derivative of Function
sin x	cos x
cos x	-sin x
tan x	sec2 x
cosec x	-cosec x cot x
sec x	sec x tan x
cot x	-cosec2 x

Proof of Differentiation of Trigonometric Functions Formula

As discussed above the formulas for all the trigonometric functions, now we will proof the above formulas of the differentiation of the trigonometric functions using first principle of derivative, quotient rule and chain rule with the help of limits.

Differentiation of sin(x)

To prove the derivative of sin x we will use the first principle of the differentiation and some basic trigonometric identities and limits formula. The trigonometric identities and limits formula which are used in the proof are given below:

1. sin (X + Y) = sin X cos Y + sin Y cos X
2. lim _x→0 [sinx / x] = 1
3. lim _{x→ 0} [(cos x – 1) / x] = 0

Let’s start the proof for the differentiation of the trigonometric function sin x

By the first principle of differentiation

(d/dx) sin x = lim _h→0 [{sin (x + h) – sin x} / {(x + h) – x}]

⇒ (d/dx) sin x = lim _h→0 [{sin x cos h + sin h cos x – sin x} / h]

⇒ (d/dx) sin x = lim _h→0 [{((cos h – 1) / h) sin x} + {(sin h / h) cos x}]

⇒ (d/dx) sin x = lim _h→0 [{(cos h – 1) / h} sin x] + lim _h→0 [(sin h / h) cos x]

⇒ (d/dx) sin x = 0.sin x + 1.cos x [By using 2 and 3]

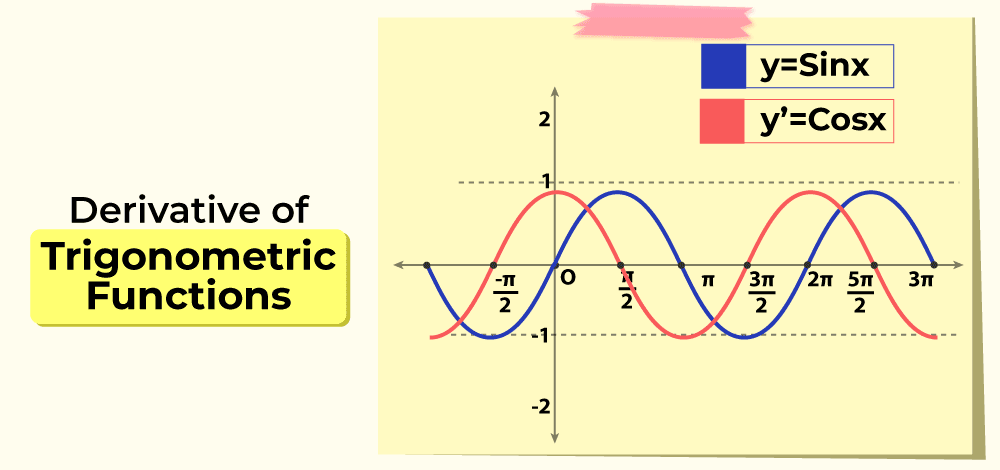
⇒ (d/dx) sin x = cos x

Therefore, differentiation of sin x is cos x. 

Differentiation of cos(x)

To prove the derivative of cos x we will use the first principle of the differentiation and some basic trigonometric identities and limits formula. The trigonometric identities and limits formula which are used in the proof are given below:

1. cos (X + Y) = cos X cos Y – sin X sin Y
2. lim _x→0 [sinx / x] = 1
3. lim _{x→ 0} [(cos x – 1) / x] = 0

Let’s start the proof for the differentiation of the trigonometric function cos x

By the first principle of differentiation

(d/dx) cos x = lim _h→0 [{cos (x + h) – cos x} / {(x + h) – x}]

⇒ (d/dx) cos x = lim _h→0 [{cos x cos h – sin h sin x – cos x} / h]

⇒ (d/dx) cos x = lim _h→0 [{((cos h – 1) / h) cos x} – {(sin h / h) sin x}]

⇒ (d/dx) cos x = lim _h→0 [{(cos h – 1) / h} cos x] – lim _h→0 [(sin h / h) sin x]

⇒ (d/dx) cos x = 0.cos x – 1.sin x [By using 2 and 3]

⇒ (d/dx) cos x = -sin x

Therefore, differentiation of cos x is -sin x.

Differentiation of tan(x)

To prove the derivative of tan x we will use the quotient rule and some basic trigonometric identities and limits formula. The trigonometric identities and limits formula which are used in the proof are given below:

1. tan x = sin x / cos x
2. sec x = 1 / cos x
3. cos² x + sin² x = 1
4. (d/dx) sin x = cos x
5. (d/dx) cos x = -sin x

Let’s start the proof for the differentiation of the trigonometric function tan x

Since, by (1)

tan x = sinx / cos x

⇒ (d/dx) tan x = (d/dx)[sinx / cos x]

By using quotient rule

(d/dx) tan x = [{(d/dx)sinx} cosx – {(d/dx) cos x} sinx] / cos²x

⇒ (d/dx) tan x = [cos x cos x – (-sin x) sin x] / cos²x [By 4 and 5]

⇒ (d/dx) tan x = [cos²x + sin²x] / cos²x

⇒ (d/dx) tan x = 1 / cos²x [By 3]

⇒ (d/dx) tan x = sec²x [By 2]

Therefore, differentiation of tan x is sec² x.

Differentiation of cosec(x)

To prove the derivative of cosec x we will use the chain rule and some basic trigonometric identities and limits formula. The trigonometric identities and limits formula which are used in the proof are given below:

1. cot x = cos x / sin x
2. cosec x = 1 / sin x
3. (d/dx) sin x = cos x

Let’s start the proof for the differentiation of the trigonometric function cosec x

(d/dx) cosec x = (d/dx) [1 / sin x] [By 2]

Using chain rule

(d/dx) cosec x = [-1 / sin²x] (d/dx) sin x

⇒ (d/dx) cosec x = [-1 / sin²x] cos x

⇒ (d/dx) cosec x = -[1 / sinx] [cos x / sin x]

⇒ (d/dx) cosec x = – cosec x cot x [By 1 and 2]

Therefore, the differentiation of cosec x is – cosec x cot x.

Differentiation of sec(x)

To prove the derivative of sec x we will use the quotient rule and some basic trigonometric identities and limits formula. The trigonometric identities and limits formula which are used in the proof are given below:

1. tan x = sin x / cos x
2. sec x = 1 / cos x
3. (d/dx) cos x = -sin x

Let’s start the proof for the differentiation of the trigonometric function sec x

(d/dx) sec x = (d/dx) [1 / cos x] [By 2]

Using chain rule

(d/dx) sec x = [-1 / cos²x] (d/dx) cos x

⇒ (d/dx) sec x = [-1 / cos²x] (-sin x)

⇒ (d/dx) sec x = [1 / cos x] [sin x / cos x]

⇒ (d/dx) sec x = sec x tan x [By 1 and 2]

Therefore, the differentiation of sec x is sec x tan x.

Differentiation of cot(x)

To prove the derivative of cot x we will use the quotient rule and some basic trigonometric identities and limits formula. The trigonometric identities and limits formula which are used in the proof are given below:

1. cot x = cos x / sin x
2. cosec x = 1 / sin x
3. cos² x + sin² x = 1
4. (d/dx) sin x = cos x
5. (d/dx) cos x = -sin x

Let’s start the proof for the differentiation of the trigonometric function cot x

Since, by (1)

cot x = cos x / sin x

(d/dx) cot x = (d/dx)[cosx / sin x]

By using quotient rule

(d/dx) cot x = [{(d/dx)cosx} sin x – {(d/dx) sin x} cos x] / sin²x

⇒ (d/dx) cot x = [(-sinx) sin x – (cosx) cos x] / sin²x [By 4 and 5]

⇒ (d/dx) cot x = [ -sin²x – cos² x] / sin²x

⇒ (d/dx) cot x = -[ sin²x + cos²x] / sin²x

⇒ (d/dx) cot x = -1 / sin²x [By 3]

⇒ (d/dx) cot x = -cosec²x [By 2]

Therefore, differentiation of cot x is -cosec² x.

Some Other Trig Function Derivatives

The differentiation of the trigonometric functions can be easily done using chain rule. The complex trigonometric functions and composite trigonometric functions can be solved by applying chain rule of differentiation. In the following headings we will further study about the chain rule and composite trig functions differentiation in detail.

• Differentiation using Chain Rule
• Differentiation of Composite Trig Function

Let’s discuss these topics in detail.

Chain Rule and Trigonometric Function

The chain rule states that if p(q(x)) is a function then, the derivative of this function is given by the product of the derivative of p(q(x)) and derivative of q(x). The chain rule is used to differentiate composite functions. The chain rule is mostly used to differentiate the composite trig functions easily.

Example: Find the derivative of f(x) = tan 4x

Solution:

f(x) = tan 4x

⇒ f'(x) = (d/dx) [tan 4x]

By applying chain rule

f'(x) = (d/dx) [tan 4x](d/dx)[4x]

⇒ f'(x) = (sec² 4x)(4)

Differentiation of Composite Trig Function

To evaluate the differentiation of the composite trig functions we apply chain rule of differentiation. The composite trig functions are the functions in which the angle of the trigonometric function is itself a function. The differentiation of composite trigonometric functions can be easily evaluated by applying the chain rule and the differentiation formulas for trig functions.

Example: Find the derivative of f(x) = cos(x² +4)

Solution:

f(x) = cos(x² +4)

⇒ f'(x) = (d/dx) cos(x² +4)

By applying chain rule

f'(x) = (d/dx) [cos(x² +4)](d/dx)[x² +4]

⇒ f'(x) = -(2x)sin(x² +4)

What are Inverse Trigonometric Functions?

The inverse trigonometric functions are the inverse functions of the trigonometric functions. There are six inverse trigonometric functions: sin^-1, cos^-1, tan^-1, cosec^-1, sec^-1, cot^-1. The inverse trigonometric functions are also called as arc functions.

Differentiation of Inverse Trigonometric Functions

The derivatives of six inverse trigonometric functions are as follows:

Function	Derivative of Function
sin-1 x	1/√(1 – x2)
cos-1 x	-1/√(1 – x2)
tan-1 x	1/(1 + x2)
cosec-1 x	1/[|x|√(x2 – 1)]
sec-1 x	-1/[|x|√(x2 – 1)]
cot-1 x	-1/(1 + x2)

Example: Find the derivative of f(x) = 3sin^-1x + 4cos^-1x

Solution:

f'(x) = (d/dx) [3sin^-1x + 4cos^-1x]

⇒ f'(x) = (d/dx) [3sin^-1x ]+ (d/dx) [4cos^-1x]

⇒ f'(x) = 3(d/dx) [sin^-1x ]+ 4(d/dx) [cos^-1x]

⇒ f'(x) = 3[1 / √(1 – x²)] + 4[-1 / √(1 – x²)]

⇒ f'(x) = 3[1 / √(1 – x²)] – 4[1 / √(1 – x²)]

⇒ f'(x) = [1 / √(1 – x²)] (3- 4)

⇒ f'(x) = -[1 / √(1 – x²)]

Applications on Differentiation of Trigonometric Functions

There are many different applications of the differentiation of the trigonometric functions in real life. The following are the applications of the differentiation of the trigonometric functions.

• The slope of the tangent and the normal line to the trigonometric curve can be determined using the differentiation of the trigonometric functions.
• It can be also used to determine the maxima and minima of the function.
• It is also used in the field of computers and electronics.

Also,Check

• Inverse Trig Derivative
• Antiderivative
• Differentiation & Integration Formulas

Sample Problems on Differentiation of Trig Functions

Problem 1: Find the derivative of f(x) = tan 2x.

Solution:

f(x) = tan 2x

⇒ f'(x) = (d/dx) tan 2x

By applying chain rule

f'(x) = (d/dx) [tan 2x](d/dx)[2x]

⇒ f'(x) = (sec²2x)(2)

⇒ f'(x) = 2sec²2x

Problem 2: Find the derivative of y = cos x / (4x²)

Solution:

y = cos x / (4x²)

Applying quotient rule

y’ = [(d/dx)cosx(4x²) – cosx (d/dx)(4x²)] / (4x²)²

⇒ y’ = [(-sinx)(4x²) – cosx (8x)] / (16x⁴)

⇒ y’ = [-4x²sinx – 8xcosx] / (16x⁴)

⇒ y’ = [-4x(xsinx + 2cosx)] / (16x⁴)

⇒ y’ = – (x sinx + 2cosx) / (4x³)

Problem 3: Evaluate the derivative f(x) = cosec x + x tan x

Solution:

f(x) = cosec x + x tan x

By applying formula and product rule

f'(x) = (d/dx) cosec x + (d /dx) [x tan x]

⇒ f'(x) = -cosec x cot x + (d /dx) x (tan x) + x (d /dx) (tan x)

⇒ f'(x) = -cosec x cot x + tan x + xsec²x

Problem 4: Find the derivative of the function f(x) = 6x⁴cos x

Solution:

f(x) = 6x⁴cos x

By applying product rule

f'(x) = (d/dx) [6x⁴cos x]

⇒ f'(x) = 6[(d/dx) (x⁴)(cos x) + (x⁴) (d/dx)(cos x)]

⇒ f'(x) = 6[ 4x³cos x + x⁴(-sin x)]

⇒ f'(x) = 6[ 4x³cos x – x⁴sin x]

⇒ f'(x) = 6x³[ 4cos x – x sin x]

Problem 5: Evaluate the derivative: f(x) = (x + cos x) (1 – sin x)

Solution:

f(x) = (x + cos x) (1 – sin x)

By applying product rule

f'(x) = (d /dx) [(x + cos x) (1 – sin x)]

⇒ f'(x) = [(d /dx) (x + cos x)] (1 – sin x) + (x + cos x) [(d /dx) (1 – sin x)]

⇒ f'(x) = [(1 – sin x) (1 – sin x)] + [(x + cos x) (0 – cos x)]

⇒ f'(x) = (1 – sin x)² – (x + cos x) cos x

⇒ f'(x) = 1 + sin²x – 2 sinx – x cosx – cos²x

Practice Problems on Differentiation of Trigonometric Functions

Problem 1: Find the derivative of y = sin(x) + cos(x).

Problem 2: Calculate the derivative of y = 2sin(x) – 3cos(x).

Problem 3: Find the derivative of y = 2sin(3x).

Problem 4: Determine the derivative of y = tan(5x).

Problem 5: Find the derivative of y = sin(x) cos(x).

Problem 6: Calculate the derivative of y = cos²(x).

Problem 7: Determine the derivative of y = tan²(x).

Problem 8: Determine the derivative of y = tan(x) sec(x).

Differentiation of Trigonometric Functions – FAQs

1. What is Differentiation?

Differentiation is a mathematical operation that calculates the rate at which a function changes with respect to its independent variable.

2. What is Trigonometric Function?

Trigonometric functions are mathematical functions that relate the angles of a right triangle to the ratios of its sides. 

3. What are Common Trigonometric Functions?

Common trigonometric functions include sine (sin), cosine (cos), tangent (tan), cosecant (cosec), secant (sec), and cotangent (cot).

4. Define the Differentiation of Trigonometric Functions.

The method of differentiating the trigonometric functions is called differentiation of trigonometric functions.

5. How do you Differentiate the Sine Function i.e., sin (x)?

The derivative of sin (x) is cos (x). In mathematical notation, d/dx(sin(x)) = cos(x).

6. What do we Get after Differentitaion of the Cosine Function i.e., cos (x)?

The derivative of cos (x) is -sin (x). In mathematical notation, d/dx(cos(x)) = -sin(x).

7. How do you Differentiate the Tangent Function i.e., tan (x)?

The derivative of tan(x) is sec²(x), where sec(x) is the secant function. In mathematical notation, d/dx(tan(x)) = sec²(x).

8. What are the Formulas for Differentiation of Trigonometric Functions?

The formula for the differentiation of trigonometric functions are:

• (d/dx) sin x = cos x
• (d/dx) cos x = -sin x
• (d/dx) tan x = sec² x
• (d/dx) cosec x = -cosec x cot x
• (d/dx) sec x = sec x tan x
• (d/dx) cot x = -cosec² x

9. Give one Example of Differentiating a Trigonometric Function.

Let’s consider a function f(x) = 2sin(3x). 

Using the chain rule, 

f'(x) = d/dx(2sin(3x)) 

⇒ f'(x) = 2 cos(3x) × 3 

⇒ f'(x) = 6cos(3x)

10. What Methods are Used to Derive the Differentiation of Trigonometric Functions?

The different ways in which the differentiation of trigonometric functions formula can be derived are:

• By using the First Principle of the Derivatives
• By using the Quotient Rule
• By using the Chain Rule

11. What is Anti Differentiation of the Trigonometric Functions?

The anti-differentiation of the trigonometric functions means finding the integration of the trigonometric functions.