What are the six trigonometry functions?
Last Updated :
27 Mar, 2024
Trigonometry can be defined as the branch of mathematics that determines and studies the relationships between the sides of a triangle and angles subtended by them. Trigonometry is basically used in the case of right-angled triangles. Trigonometric functions define the relationships between the 3 sides and the angles of a triangle. There are 6 trigonometric functions mainly. Before going into the study of the trigonometric functions we will learn about the 3 sides of a right-angled triangle.

The three sides of a right-angled triangle are as follows,
- Base The side on which the angle θ lies is known as the base.
- Perpendicular It is the side opposite to the angle θ in consideration.
- Hypotenuse It is the longest side in a right-angled triangle and opposite to the 90° angle.
Trigonometric Functions
Trigonometry has 6 basic trigonometric functions, they are sine, cosine, tangent, cosecant, secant, and cotangent. Now let’s look into the trigonometric functions. The six trigonometric functions are as follows,
- sine It is represented as sin θ and is defined as the ratio of perpendicular and hypotenuse.
- cosine It is represented as cos θ and is defined as the ratio of base and hypotenuse.
- tangent It is represented as tan θ and is defined as the ratio of sine and cosine of an angle. Thus the definition of tangent comes out to be the ratio of perpendicular and base.
- cosecant It is the reciprocal of sin θ and is represented as cosec θ.
- secant It is the reciprocal of cos θ and is represented as sec θ.
- cotangent It is the reciprocal of tan θ and is represented as cot θ.
What are the six trigonometry functions?
The six trigonometric functions have formulae for the right-angled triangles, the formulae help in identifying the lengths of the sides of a right-angled triangle, lets take a look at all those formulae,

| Trigonometric Functions | Formulae |
| sin θ | 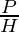 |
| cos θ | 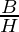 |
| tan θ | 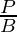 |
| cosec θ | 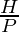 |
| sec θ | 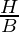 |
| cot θ | 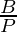 |
The below table shows the values of these functions at some standard angles,
| Function | 0° | 30° | 45° | 60° | 90° |
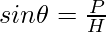 |  | 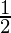 | 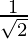 | 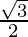 | 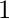 |
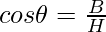 | 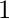 | 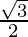 | 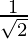 | 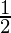 | 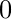 |
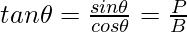 | 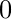 | 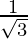 | 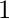 | 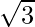 | ∞ |
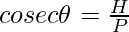 | ∞ | 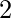 | 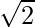 | 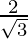 | 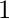 |
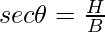 | 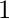 | 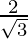 | 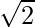 | 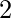 | ∞ |
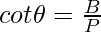 | ∞ | 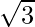 | 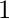 | 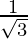 | 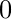 |
Note: It is advised to remember the first 3 trigonometric functions and their values at these standard angles for ease of calculations.
Sample Problems
Question 1: Evaluate sine, cosine, and tangent in the following figure.

Solution:
Given 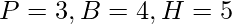
Using the trigonometric formulas for sine, cosine and tangent,
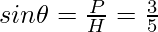
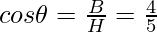
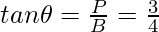
Question 2: In the same triangle evaluate secant, cosecant, and cotangent.
Solution:
As it is known the values of sine, cosine and tangent, we can easily calculate the required ratios.
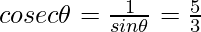
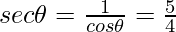

Question 3: Given 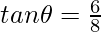 , evaluate sin θ.cos θ.
, evaluate sin θ.cos θ.
Solution:
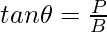
Thus P=6, B=8
Using Pythagoras theorem,
H2=P2+B2
H2=36+64=100
Therefore, H =10
Now, 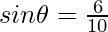
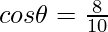
Question 4: If 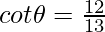 , evaluate tan2θ.
, evaluate tan2θ.
Solution:
Given 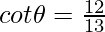
Thus 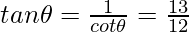
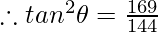
Question 5: In the given triangle, verify sin2θ+cos2θ = 1

Solution:
Given P=12, B=5, H=13
Thus 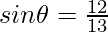
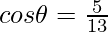
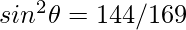
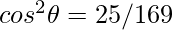
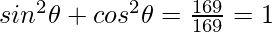
Hence verified.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...