We see solids everywhere where we look. Most of the time these solids are either in the shape of a cube, cylinder, and cone, etc., or in the shape that combines these shapes. It is essential in many of the real-life problems for us to know how to calculate the area and volume of these shapes. For example, a painter might want to know the area he/she has to paint for the given shape. Similarly, before making a metal sphere ball, we need to know how much material will be required. All these things require some knowledge of the volume and surface areas of the basic shapes. Let’s see them in detail.
Surface Area and Volume of Solid Shapes
The surface area is the area that describes the amount of material used to cover a geometric solid while the volume can be defined as a measure of how much space the solid takes. It is essential to know the formulas for calculating the areas and volumes for basic shapes. Let’s look at the surface of the following shapes:
Cuboid
The figure below shows the cuboid shape, this is the shape of our boxes, cartons, etc, our goal is to derive the formulas to calculate its surface area and the volume. Let’s say the length of the cuboid is “l”, the breadth is “b” and the height is “h”.

Surface Area of Cuboid
To calculate the surface area of the cube, let’s open it up like in the figure given below. Now the figure shows the flattened cuboid. It has 6 rectangles which correspond to the six faces of the cuboid. For the surface area of the cube, we need to find out the total area of all the rectangles.

Total surface area = Area of rectangle 1 + Area of rectangle 2 + Area of rectangle 3 + Area of rectangle 4 + Area of rectangle 5 + Area of rectangle 6
⇒ (l × h) + (l × b) + (l × h) + (l × b) + (b × h) + (b × h)
⇒ 2(lh + lb + bh)
Thus, the surface area of cuboid = 2 (lh + lb + bh)
Volume of Cuboid
We know that the volume of a region is given by its magnitude, that is how much space it takes.
The volume of a cuboid = base area x height
= l × b × h
= lbh
Cube
Cube is a solid shape with has all of its sides of equal length. We know that a cube is just a cuboid with all the sides equal. Our goal is to derive the formulas for calculating the surface area and the volume of the cube. The figure below represents a cube. Notice that all the sides are equal, and it looks similar to the cuboid. A cube is basically a cuboid that has all of its sides of equal length. That is,
l = b = h = a
Where “a” is the length of the side of the cube.

Surface Area of Cube
Thus, putting this in the above formula
Surface area of cube = 2(a2 + a2 + a2)
⇒ 2(3a2) = 6a2
Volume of Cube
Similar to above method, let’s substitute the length of side in the formula.
Volume = lbh
= aaa
= a3
Right Circular Cylinder
The cola cans we use are an example of a right circular cylinder. It can also be found in other places in our lives, for example, our pens also look similar to cylinders. The figure below shows a cylinder and its unrolled version which will be used for calculating surface area. Let’s say the height of the cylinder is “h” and its radius is “r”.

Surface Area of Cylinder
The figure above shows a cylinder when it is unrolled. It becomes easy to find its surface area once it is unrolled. Notice that the cylinder once unrolled looks like a rectangle. The breadth of the rectangle will be given by “h” but the length is given by the circumference of the cylinder.
Circumference of the cylinder = 2πr
Area of the rectangle = 2πrh
Thus, the Surface area of the Right Circular Cylinder = 2πrh
Total surface area of the right circular cylinder = Surface Area of the cylinder + Area of base
= 2πrh + 2πr2 = 2πr(r+h)
Volume of Cylinder
Volume of cylinder = base area x height
= πr2 × h
= πr2 h
Sphere
A sphere is a three-dimensional figure (solid figure), which is made up of all points in the space, which lie at a constant distance called the radius, from a fixed point called the Centre of the sphere. The figure below shows a sphere, and its flattened version when it is cut. This is used to calculate the surface area of the sphere.

Surface Area of a Sphere
As similar to the above cases, we will cut the sphere and flatten it.
In the figure, we can see that when a sphere is cut, it generates an area equivalent to four spheres.
Thus, the surface area of the sphere = 4πr2
Volume of the Sphere
This formula is proved experimentally, so we cannot present any proof here.
Volume of Sphere = 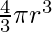
Cone
A cone is a three-dimensional figure having the base as a circle and the height tapers and meets at a point in the end. Apex is the name of the pointed end of the cone, we see a lot of shapes in form of a cone in our everyday life, for example, the ice cream is in the shape of a cone, etc.
In the figure below, the cone has a radius of “r”, and a height of “h”.

Surface Area of Cone
The surface area of the cone is given by
Curved surface Area of cone = 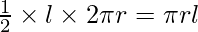
Where, 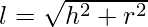
Volume of Cone
The volume of the cone is given by,
Volume of Cone = 
Hemisphere
Imagine a plane dividing the sphere in two equal parts, each part is known as a Hemisphere. The term hemisphere is used to explain the different parts on the globe, Northern Hemisphere, Southern Hemisphere, eastern hemisphere, western hemisphere.

Surface Area of a Hemisphere
Since a Hemisphere is half a sphere, The surface area will be half as well but along with that, a base in the shape of a circle is also visible that too is included in the surface area of the hemisphere.
Therefore, the surface area of a hemisphere= 2πr2+πr2
= 3πr2
Volume of a Hemisphere
The Volume of the hemisphere will be half the volume of sphere.
Volume of hemisphere= 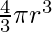
Prism
A Prism is a three-dimensional figure having two bases facing each other, these bases can be the shape of a triangle, rectangle, or any polygon. The material of prism is mostly fluorite, glass, plastic.
The base of the prism can be regular or irregular, if the base is irregular, it is called as irregular prism. If the base of the prism is regular, the prism is a regular prism.
Surface area of the Prism
Let’s look at the surface area of the Triangular prism,
Surface area of the prism= 2(area of triangular bases) + (area of rectangle with base b and length l) +2(area of rectangle with side s and length l).

Surface area of the Prism= 2(1/2 ×b× h) +2(s× l) +(b×l)
= (b×h) + 2(s×l) + (l×b)
Volume of the prism
The volume of the prism is the area of the square multiplied by the height/length of the prism,

Volume of Prism= 1/2 bhl
Let’s see some sample problems on these concepts
Sample Problems
Question 1: Find the volume and surface area of a cube whose side is a = 10cm.
Solution:
We know the formulas for surface areas and volume.
Surface Area = 6a2
= 6(10)2 {Given a = 10cm}
= 6 (100)
= 600 cm2
Volume of the cube = a3
= (10)3
= 1000 cm3
Question 2: Find the volume and surface area of the water tank which is in the shape of a cylinder with a radius of 10m and height of 40m.
Solution:
We know the formulas for surface areas and volume for cylinder.
r = 10 and h =40.
Surface Area of the cylinder = Curved Surface Area + Area of bases

Volume of the Cylinder,

Question 3: Find the volume and surface area of an ice cream cone whose radius is 3cm and height is 4cm.

Solution:
An ice cream cone is basically a cone. We need to find the area and the volume for that cone. Since the cone is not closed from the top, we only need to find the curved surface area.
Surface Area of cone,
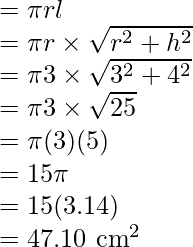
Volume of the cone,
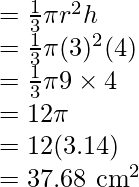
Question 4: Find the volume and surface area of the sphere whose radius is 10cm.
Solution:
Given r = 10cm.
Surface Area
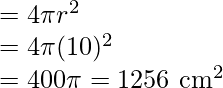
Volume

Question 5: Find the surface area of the hemisphere with radius 7cm, also find the volume.
Solution:
Surface area of the hemisphere= 
= 3× 22/7× (7×7)
=462 cm2
Volume of hemisphere

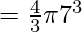
= 1437.333 cm3
Question 6: Find the surface area of a triangular prism mentioned in the figure below,

Solution:
Surface area of the Prism = (b×h) + 2(l×s)+ (l×b)
= (5×5)+ 2(7×10) +(5×10)
= 25+ 140+ 50
= 75+ 140
= 215cm2
Share your thoughts in the comments
Please Login to comment...