Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.4

This exercise has been deleted as per new NCERT Syllabus

Question 1. Let ∆ ABC ~ ∆ DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.

Solution:

According to the theorem 1, we get

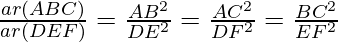
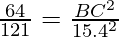
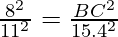
BC = 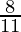 × 15.4

BC = 11.2 cm

Question 2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD. 

Solution:

Given, ABCD is a trapezium with AB || DC. Diagonals AC and BD intersect each other at point O.

In △AOB and △COD,

∠ AOB = ∠ COD (Opposite angles)

∠ 1 = ∠ 2 (Alternate angles of parallel lines)

△AOB ~ △COD by AA property.

According to the theorem 1, we get

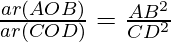
As, AB = 2CD

= 

= 

= 

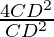
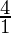
ar(AOB) : ar(COD) = 4 : 1

Question 3. In Figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that .

Solution:

Let’s draw two perpendiculars AP and DM on line BC.

Area of triangle = ½ × Base × Height

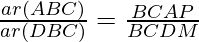
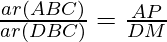 ……………………………(1)

In ΔAPO and ΔDMO,

∠APO = ∠DMO (Each 90°)

∠AOP = ∠DOM (Vertically opposite angles)

ΔAPO ~ ΔDMO by AA similarity

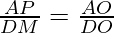 ……………………………(2)

From (1) and (2), we can conclude that

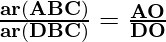
Question 4. If the areas of two similar triangles are equal, prove that they are congruent.

Solution:

As it is given, ΔABC ~ ΔDEF

According to the theorem 1, we have

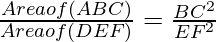
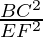 =1 [Since, Area(ΔABC) = Area(ΔDEF)

BC² = EF²

BC = EF

Similarly, we can prove that

AB = DE and AC = DF

Thus, ΔABC ≅ ΔPQR [SSS criterion of congruence]

Question 5. D, E and F are respectively the mid-points of sides AB, BC, and CA of ∆ ABC. Find the ratio of the areas of ∆ DEF and ∆ ABC.

Solution:

As, it is given here

DF = ½ BC

DE = ½ AC

EF = ½ AB

So,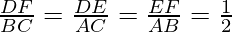 

Hence, ΔABC ~ ΔDEF

According to theorem 1,

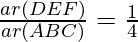
ar(ΔDEF) : ar(ΔABC) = 1 : 4

Question 6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Solution:

Given: AM and DN are the medians of triangles ABC and DEF respectively.

ΔABC ~ ΔDEF

According to theorem 1,

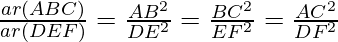
So,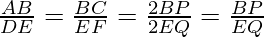 

 ……………………….(1)

∠B = ∠E (because ΔABC ~ ΔDEF)

Hence, ΔABP ~ ΔDEQ [SAS similarity criterion]

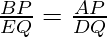 ……………………….(2)

From (1) and (2), we conclude that

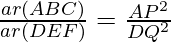
Hence, proved!

Question 7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.

Solution:

Let’s take side of square = a

Diagonal of square AC = a√2

As, ΔBCF and ΔACE are equilateral, so they are similar

ΔBCF ~ ΔACE

According to theorem 1,

=

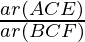 = 2

Hence, Area of (ΔBCF) = ½ Area of (ΔACE)

Tick the correct answer and justify:

Question 8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is

(A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4

Solution:

Here,

AB = BC = AC = a

and, BE = BD = ED = ½a

ΔABC ~ ΔEBD (Equilateral triangle)

According to theorem 1,

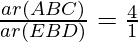
Area of (ΔABC) : Area of (ΔEBD) = 4 : 1

Hence, OPTION (C) is correct.

Question 9. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio

(A) 2 : 3 (B) 4 : 9 (C) 81 : 16 (D) 16 : 81 

Solution:

ΔABC ~ ΔDEF

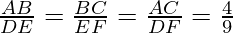
According to theorem 1,

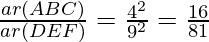
Area of (ΔABC) : Area of (ΔDEF) = 16 : 81

Hence, OPTION (D) is correct.