Question 15. Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm, find the length of the other diagonal.
Solution:

Given,
In rhombus ABCD, diagonals AC and BD bisect each other at O at right angles
Each side = 10 cm and one diagonal AC = 16 cm
∴ AO = OC = 16/2 = 8 cm
Now in ∆AOB,
By using Pythagoras theorem
AB2 = AO2 + OB2
(10)2 = (8)2 + (BO)2
100 = 64 + BO2
BO2 = 100 – 64 = 36
BO = 6
So, BD = 2BO = 2 x 6 = 12 cm
Hence, the length of the other diagonal is 12 cm
Question 16. Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
Solution:

Given,
Side of equilateral triangle=12 cm
To find: Calculate the height of an equilateral triangle
Let us draw the figure. Let us draw the altitude AD.
BD = DC = 6cm [ Altitude is also median of the equilateral triangle]
In ∆ADB,
By using Pythagoras theorem
AB2 = AD2 + BD2
144 = AD2 + 36
AD2 = 144 − 36 = 108
AD = 10.39 cm
Hence, the height of the equilateral triangle is 10.39 cm
Question 17. In the figure, ∠B < 90° and segment AD ⊥ BC. Show that:
(i) b2 = h2 + a2 + x2 – 2ax
(ii) b2 = a2 + c2 – 2ax
Solution:

Given : In ∆ABC, ∠B < 90°
AD ⊥ BC
AD = c, BC = a, CA = b AD = h, BD = x, DC = a – x
(i) In ∆ADC,
By using Pythagoras theorem
AC2 = AD2 + DC2
b2 = h2 + (a – x)2
So, b2 = h2 + a2 + x2 – 2ax
(ii) Similarly in right ∆ADB
By using Pythagoras theorem
AB2 = AD2 + BD2
c2 = h2 + x2 …..….(i)
b2 = h2 + a2 + x2 – 2ax
= h2 + x2 + a2 – 2ax
= c2 + a2 – 2ax [From eq(i)]
So, b2 = a2 + c2 – 2ax
Hence proved.
Question 18. In an equilateral ∆ABC, AD ⊥ BC, prove that AD2 = 3 BD2.
Solution:

In right-angled ∆ABD,
By using Pythagoras theorem
AB2 = AD2 + BD2 ….(1)
We know that in an equilateral triangle every altitude is also median.
So, AD bisects BC.
We have BD = DC
Since ∆ABC is an equilateral triangle, AB = BC = AC
So, we can write equation (1) as
BC2 = AD2 + BD2 ….(2)
But BC = 2BD
Therefore, equation (2) becomes,
(2BD)2 = AD2 + BD2
On simplifying the equation we get,
4BD2 – BD2 = AD2
3BD2 = AD2
So, AD2 = 3BD2
Hence proved
Question 19. ∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC.BD
(ii) AC2 = BC.DC
(iii) AD2 = BD.CD
(iv) AB2/AC2 = BD/DC
Solution:

(i) In ΔADB and ΔCAB
∠DAB = ∠ACB = 90°
∠ABD = ∠CBA (common angle)
∠ADB = ∠CAB (remaining angle)
So, by AAA
ΔADB ~ ΔCAB
Hence,
AB/CB = BD/AB
⇒ AB2 = CB × BD
(ii) Let ∠CAB = y
In ΔCBA
∠CBA = 180° − 90° − y
∠CBA = 90° − y
Similarly, in ΔCAD
∠CAD = 90° − ∠CAD = 90° − y
∠CDA = 90° − ∠CAB
= 90° − y
∠CDA = 180° −90° − (90° − y)
∠CDA = y
Now in ΔCBA and ΔCAD,
∠CBA = ∠CAD
∠CAB = ∠CDA
∠ACB = ∠DCA = 90°
So, by AAA rule
ΔCBA ~ ΔCAD
So, AC /DC = BC/AC
⇒ AC2 = DC × BC
(iii) In ΔDCA & ΔDAB
∠DCA = ∠DAB (both are equal to 90°)
∠CDA = ∠ADB (common angle)
∠DAC = ∠DBA (remaining angle)
So, by AAA rule
ΔDCA ~ ΔDAB
so, DC/DA = DA/DB
⇒ AD2 = BD × CD

(iv) From part (i) AB2 = CB x BD
From part (ii) AC2 = DC × BC
So, AB2/AC2= CB x BD/DC x BC
AB2/AC2 = BD/DC
Hence proved
Question 20. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution:

Given,
AC = 18m be the height of pole.
BC = 24m is the length of a guy wire and is attached to stake B.
Now,
In △ABC
By using Pythagoras theorem
BC2 = AB2 + AC2
242 = AB2 + 182
AB2 = 576 − 324
= 252
So, AB = 6√7 m
Hence, the stake has to be 6√7 m from base A.
Question 21. Determine whether the triangle having sides (a – 1) cm, 2 √a cm and (a + 1) cm is a right-angled triangle.
Solution:

Given,
The sides of triangle are (a – 1) cm, 2√a and (a + 1) cm.
Let us considered ABC be the triangle in which with the sides are
AB = (a – 1)cm, BC = (2√ a) cm, CA = (a + 1) cm
AB² = (a – 1)2
By using (a – b)2 = a2 + b2 – 2ab
= a2 + 12 – 2 × a × 1
AB2 = a2 + 1 -2a
BC2 = (2√a)2
∴ BC = 4a
CA2 = (a + 1)2
By using (a + b)2 = a2 + b2 + 2ab
= a2 + 12 + 2 × a × 1
CA2 = a2+ 1 + 2a
By using Pythagoras Theorem
AC2 = AB2 + BC2
On putting value of AC2, AB2 and BC2 in the above equation,
a2 + 1 + 2a = a2 + 1 – 2a + 4a
a2 + 1 + 2a = a2 + 1 + 2a
AC2 = AB2 + BC2
∆ABC is right-angled ∆ at B.
Hence proved
Question 22. In an acute-angled triangle, express a median in terms of its sides.
Solution:

Given,
In Δ ABC AD is median.
Construction: AE ⊥ BC
Now,
∴ BD = CD = 1/2 BC ….(1) [AD is the median]
In Δ AED,
By using Pythagoras Theorem
AD2 = AE2 + DE2
⇒ AE2 = AD2 – DE2 …..(2)
In Δ AEB,
AB2 = AE2 + BE2
⇒ AD2 – DE2 + BE2 [From eq(2)]
= (BD + DE)2 + AD2 – DE2 [∴ BE = BD + DE]
BD2 + DE2 + 2BD x DE + AD2 – DE2
= BD2 + AD2 + 2BD x DE
= (1/2BC)2 + AD2 + (2 × 1/2BC × DE) [From eq(1)]
= (1/4BC)2 + AD2 + BC x DE ….(3)
In Δ AED,
By using Pythagoras Theorem
AC2 = AE2 + EC2
= AD2 – DE2 + EC2
= AD2 – DE2 + (DC – DE)2
= AD2 – DE2 + DC2 + DE2 – 2DC x DE
AD2 + DC2 – 2DC x DE
= AD2 + (1/2BC)2 – (2 × 1/2BC x DE)
= AD2 + (1/4BC)2 – BC x DE ….(4)
On adding eq(3) and (4), we get
AB2 + AC2 = 1/4BC2 + AD2 + BC x DE + AD2 + 1/4BC2 – BC x DE
= 1/2BC2 + 2AD2
2(AB2 + AC2) = BC2 + 4AD2
2AB2 + 2AC2 = BC2 + 4AD2
Hence Proved
Question 23. In right-angled triangle ABC in which ∠C = 90°, if D is the mid point of BC, prove that AB2 = 4AD2 – 3AC2.
Solution:

Given :
∠C = 90° and D is the mid-point of BC.
To prove : AB2 = 4AD2 – 3AC2
In ∆ ACD,
By using Pythagoras Theorem
AD2 = AC2 + CD2
CD2 = AD2 – AC2 ……….(1)
In ∆ACB,
By using Pythagoras Theorem
AB2 = AC2 + BC2
AB2 = AC2 + (2CD)2 [D is the mid-point of BC]
AB2 = AC2 + 4CD2
∴ AB2 = AC2 + 4(AD2 – AC2) [From eq(1)]
AB2 = AC2 + 4AD2 – 4AC2
AB2 = 4AD2 – 4AC2 + AC2
∴ AB2 = 4AD2 – 3AC2
Hence Proved
Question 24. In the figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that
(i) b2 = p2 + a2/4 + ax
(ii) c2 = p2– ax + a2/4
(iii) b2 + c2 = 2p2 + a2/2
Solution:

Given,
D is the midpoint of BC
(i) In ∆ AEC
AC2 = AE2 + EC2
b2 = AE2 + (ED + DC)2
b2 = AD2 + DC2 + 2 x ED x DC [Given BC = 2CD]
b2 = p2 + (a/2)2 + 2(a/2)x
b2 = p2 + a2/4 + ax ………..(i)
(ii) In ∆ AEB
AB2 = AE2 + BE2
c2 = AD2 – ED2 + (BD – ED)2
c2 = p2 – ED2 + BD2 + ED2 – 2BD x ED
c2 = P2 + (a/2)2 – 2(a/2)2x
c2 = p2 – ax + a2/4 ……………….(ii)
(iii) Adding eqn (i) and (ii) we get,
b2 + c2 = 2p2 + a2/2
Hence Proved
Question 25. In ∆ABC, ∠A is obtuse, PB x AC and QC x AB. Prove that:
(i) AB x AQ = AC x AP
(ii) BC2 = (AC x CP + AB x BQ)
Solution:

(i) Given :
∠A is obtuse.
PB is perpendicular to AC.
QC is perpendicular to AB.
To Prove :
AB × AQ = AC × AP.
Proof:
In ΔACQ and ΔABP,
⇒ ∠CAQ = ∠BAP [Vertically opposite ∠]
⇒ ∠Q = ∠P [∠Q = ∠P = 90 º]
So, by AA rule
ΔACQ ~ ΔABP
By Property of Similar Triangles,
⇒ CQ/BP = AC/AB = AQ/AP
⇒ AC/AB = AQ/AP
⇒ AB × AQ = AC × AP ……..(i)
Hence Proved.
(ii) To Prove :
BC² = AB × BQ + AC × CP
Proof:
By using Pythagoras Theorem
⇒ BC2 = CQ2 + QB2
⇒ BC2 = CQ2 + (QA + AB)2
⇒ BC2 = CQ2 + QA2 + AB2 + 2 QA × AB
⇒ BC2 = CQ2 + QA2 + AB2 + QA × AB + QA × AB
⇒ BC2 = AC2 + AB2 + QA × AB + QA × AB [In ΔACQ, CQ2 + QA2 = AC2]
⇒ BC2 = AC2 + AB2 + QA × AB + AC × CP [By Eq (i)]
⇒ BC2 = AC2 + AC × CP + AB² + QA × AB
⇒ BC2 = AC × (AC + CP) + AB × (QA + AB)
⇒ BC2 = AC × CP + AB × BQ [CP = AC + CP, BQ = AQ + AB]
⇒ BC2 = AB × BQ + AC × CP.
Hence, Proved.
Question 26. In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4 (AD2 – AC2).
Solution:

Given:
∠C = 90°
In ∆ADC
By using Pythagoras Theorem
AD2 = AC2 + DC2
AD2 = AC2 + (1/2BC)2 [DC = 1/2BC]
AD2 = AC2 + 1/4(BC)2
4AD2 = 4AC2 + (BC)2
-(BC)2 = 4AC2 – 4AD2
Taking minus common
(BC)2 = 4(AD2 – AC2)
Hence, proved
Question 27. In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
Solution:

Given: ABCD is a quadrilateral, ∠B = 90° and AD2 = AB2 + BC2 + CD2
To prove: ∠ACD = 90°
Proof: In right ∆ABC,
By using Pythagoras Theorem
AC2 = AB2 + BC2 … (1)
Given, AD2 = AB2 + BC2 + CD2
⇒ AD2 = AC2 + CD2 [Using eq(1)]
In ∆ACD,
AD2 = AC2+ CD2
So, ∠ACD = 90° [By converse of Pythagoras theorem]
Question 28. An aeroplane leaves an airport and flies due north at a speed of 1000 km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/ hr. How far apart will be the two planes after 1and1/2 hours?
Solution:

Given that speed of first aeroplane = 1000 km/hr
Distance travelled by first aeroplane (due north) in 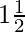 hours = 1000 x 3/2 km = 1500 km
hours = 1000 x 3/2 km = 1500 km
Speed of second aeroplane = 1200 km/hr
Distance travelled by first aeroplane (due west) in 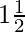 hours = 1200 × 3/2 km = 1800 km
hours = 1200 × 3/2 km = 1800 km
Now in ΔAOB,
Using Pythagoras Theorem,
AB2 = AO2 + OB2
⇒ AB2 = (1500)2 + (1800)2
⇒ AB = √(2250000 + 3240000)
= √5490000
⇒ AB = 300√61 km
Hence, in 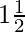 hours the distance between two plane = 300√61 km.
hours the distance between two plane = 300√61 km.
Share your thoughts in the comments
Please Login to comment...