Skip to content
Related Articles
Open in App
Not now

Related Articles

Class 10 RD Sharma Solutions – Chapter 14 Coordinate Geometry – Exercise 14.4

Improve Article
Save Article
  • Last Updated : 30 Nov, 2022
Improve Article
Save Article

Question 1. Find the centroid of the triangle whose vertices are:

(i) (1, 4), (-1, -1), and (3, -2)

Solution:

Given, vertices of triangle are (1, 4), (-1, -1), and (3, -2)

As we know that the coordinates of the centroid of a triangle whose vertices are (x1, y1), (x2, y2), (x3, y3)

(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})

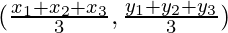
So, the coordinates of the centroid of a triangle are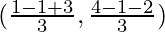(\frac{1-1+3}{3},\frac{4-1-2}{3})

= (1, 1/3)        

Hence, the centroid of the triangle whose vertices are (1, 4), (-1, -1), and (3, -2) is (1, 1/3).       

(i) (-2, 3), (2, -1), and (4, 0)

Solution:

Given, vertices of triangle are (-2, 3), (2, -1), and (4, 0)

As we know that the coordinates of the centroid of a triangle whose vertices are (x1, y1), (x2, y2), (x3, y3)

(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})

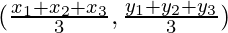
So, the coordinates of the centroid of a triangle are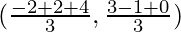(\frac{-2+2+4}{3},\frac{3-1+0}{3})

= (4/3, 2/3)        

Hence, the centroid of the triangle whose vertices are (-2, 3), (2, -1), and (4, 0) is (4/3, 2/3).  

Question 2. Two vertices of a triangle are(1, 2), (3, 5), and its centroid is at the origin. Find the coordinates of the third vertex.

Solution:

According to question 

Two vertices of a triangle are(1, 2), (3, 5), and its centroid is at the origin

Find: the coordinates of the third vertex

So, let us assume that the coordinates of the third vertex is (x, y), 

So, the coordinates of the centroid of a triangle are 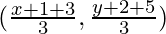(\frac{x+1+3}{3},\frac{y+2+5}{3})

 As we know that the centroid is at origin. So, 

(x + 1 + 3)/3 = 0

x + 4 = 0

x = -4

(y + 2 + 5)/3 = 0

y + 7 = 0

y = -7

Hence, the third coordinate is (-4, -7)

Question 3. Find the third vertex of a triangle, If two of Its vertices are at (−3, 1) and (0, −2) and the centroid is at the origin.

Solution:

According to the question

ABC is a triangle in which the coordinates of A are (−3, 1), B are (0, −2), and C are (a, b)

and the centroid of the triangle ABC is (0, 0)

so, 

(-3 + 0 + a)/3 = 0

a = 3

(1 – 2 + b)/3 = 0

b = 1

Hence, the coordinates of third vertex is (3, 1)

Question 4. A (3, 2) and B (−2, 1) are two vertices of a triangle ABC whose centroid G has the coordinates (5/3, -1/3). Find the coordinates of the third vertex C of the triangle.

Solution:

According to the question

ABC is a triangle in which the coordinates of A are (3, 2), B are (−2, 1), and C are (a, b)

and the centroid of the triangle ABC is (5/3, -1/3)

so, 

(3 – 2 + a)/3 = 5/3

a = 4

(1 + 2 + b)/3 = -1/3

b = -4

Hence, the coordinates of third vertex is (4, -4)

Question 5. If (−2, 3), (4, −3), and (4, 5) are the mid-points of the sides of a triangle, Find the coordinates of Its centroid.

Solution:

Let us assume ABC is a triangle 

Now in this triangle P, Q, R be the mid point of side, AC, AB, BC. 

The coordinates of P(−2, 3), Q (4, −3), and R(4, 5) 

Let us assume that the coordinates of A, B, and C are (x1, y1), (x2, y2), and (x3, y3)

As we know that P is the mid point of side AC, 

So, 

(x1 + x3) /2 = -2 

= x1 + x3 = -4 …..(1)

(y1 + y3) /2 = 3

= y1 + y3 = 6 …..(2)

As we know that Q is the mid point of side AB, 

So, 

(x1 + x2) /2 = 4 

= x1 + x2 = 8 …..(3)

(y1 + y2) /2 = -3

= y1 + y2 = -6 …..(4)

As we know that R is the mid point of side BC, 

So, 

(x2 + x3) /2 = 4 

= x2 + x3 = 8 …..(5)

(y2 + y3) /2 = 5

= y2 + y3 = 10 …..(6)

Now add c

2(x1 + x2 + x3) = -4 + 8 + 8 = 12  …..( 7)

x1 + x2 + x3 = 6

Now subtract eq(1), (3), (5) from eq(7), we get

x1 = 10

x2 = -2

x3 = -2

Similarly, add (2), (4), and (6), we get

2(y1 + y2 + y3) = -6 + 6 + 10 = 10 

y1 + y2 + y3 = 5   ……(8)

Now subtract eq(2), (4), (6) from eq(8), we get

y1 = -1

y2 = 11

y3 = -5

so, the coordinate of  ABC triangle are (10, -1), (-2, 11), and (-2, -5)

Hence, the centroid of the triangle is ((10 – 2 – 2)/3, (-1 + 11 – 5)/3)  = (2, 5/3)

Question 6. Prove analytically that the middle points of two sides of a triangle is equal to half to the third side.

Solution:

In triangle ABC,

D and E are the mid-points of the sides AB and AC 

The DE = 1/2 BC 

Let the coordinates of the vertices of a ∆ABC be (x1, y2), B(x2, y2), and C(x3, y3)

Then coordinates of D will be

(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})

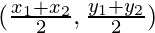
and coordinates of E will be

(\frac{x_1+x_3}{2},\frac{y_1+y_3}{2})

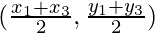
Length of BC=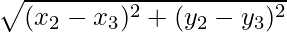\sqrt{(x_2-x_3)^2+(y_2-y_3)^2} ……(1)

and the length of DE

=\sqrt{(\frac{x_1+x_2}{2}-\frac{x_1+x_3}{2})^2+(\frac{y_1+y_2}{2}-\frac{y_1+y_3}{2})^2}\\ =\sqrt{(\frac{x_1+x_2-x_1-x_3}{2})^2+(\frac{y_1+y_2-y_1-y_3}{2})^2}\\ =\sqrt{\frac{(x_2-x_3}{2})^2+(\frac{y_2-y_3}{2})^2}\\ =\frac{1}{2}\sqrt{(x_2-x_3)^2+(y_2-y_3)^2}

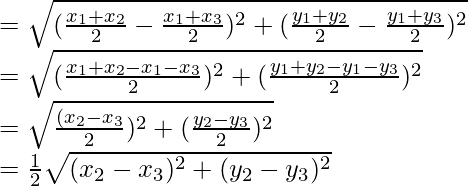
= 1/2 BC 

Hence Proved

Question 7. Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the points of its diagonals meet in a point and bisect another.

Solution:

Let us assume the vertices of ABCD quadrilateral are A (x1, y1), B (x2, y2), C (x3, y3) and D (x4, y4) 

In this quadrilateral, E and F are the mid-points of side BC and AD 

and EF is joined G and H are the mid-points of diagonal AC and BD.

GH are joined

Now co-ordinates of E will be 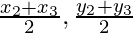\frac{x_2+x_3}{2},\frac{y_2+y_3}{2}

and co-ordinates of F will be 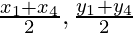\frac{x_1+x_4}{2},\frac{y_1+y_4}{2}

Co-ordinates of G will be 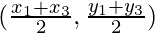(\frac{x_1+x_3}{2},\frac{y_1+y_3}{2})

Co-ordinates of H will be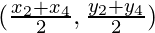(\frac{x_2+x_4}{2},\frac{y_2+y_4}{2})

Here, EF and GH intersect each other at M.

So, let M is the midpoint of EF, then its coordinates will be

(\frac{x_1+x_2+x_3+x_4}{4},\frac{y_1+y_2+y_3+y_4}{4})

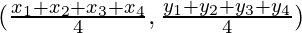
Let M is the midpoint of GH, then its coordinates of M will be

(\frac{x_1+x_2+x_3+x_4}{4},\frac{y_1+y_2+y_3+y_4}{4})

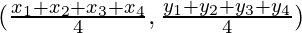
Here, we conclude that the coordinates of in both cases are same

Therefore, EF and GH bisect each other at M

Question 8. If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2 + PB2 + PC2 = GA2 + GB2 + GC2 + 3GP.

Solution:

According to the question 

ABC is a triangle, G is the centroid of it let P(h, x) is any point in the plane.

We have to prove that PA2 + PB2 + PC2 = GA2 + GB2 + GC2 + 3GP

Proof: 

In triangle ABC, 

Let us assume the coordinates of are(x1, y1) of B are(x2, y2), and of C are(x3, y3)

Therefore, co-ordinates of centroid G will be (u, v)

Where u = (x1 + x2 + 3)/3 and v = (y1 + y2 + 3)/3 

Now, we shall find L.H.S and R.H.S. separately

PA2 + PB2 + PC2 = (h – x1)2 + (k – y1)2 + (h – x2)2 + (k – y2)2 + (h – x3)2 + (k – y3)2

=3(h^2+k^2)+(x^2_1+x^2_2+x_3^2)+(y_1^2+y^2_2+y_3^2)-2h(x_1+x_2+x_3)-2k(y_1+y_2+y_3)\\ =3(h^2+k^2)+(x_1^2+x_2^2+x_3^2)+(y_1^2+y_2^2+y_3^2)-2h(3u)-2k(3v)\\ =3(h^2+k^2)-6hu-6kv+(x_1^2+x_2^2+x_3^2)+(x_1^2+x_2^2+x_3^2)GA^2+GB^2+GC^2+3GD^2\\ =(u-x_1)^2+(v-y_1)^2+(u-x_2)^2+(v-y_2)^2+(u-x_3)^2+(v-y_3)^2+3[(u-h)^2+(v-k)^2]\\

=3(u^2+v^2)+(x_1^2+y_1^2+x_2^2+y_2^2+x_3^2+y_3^2)-2u(x_1+x_2+x_3)-2v(y_1+y_2+y_3)+3(u^2+h^2-2uh+v^2+k^2-2vk)\\ =6(u^2+v^2)+(x_1^2+y_1^2+x_2^2+y_2^2+x_3^2+y_3^2)-2u(3u)-2v(3v)+3(h^2+k^2)-6uh-6vk\\ =(x_1^2+x^2_2+x_3^2)+(y_1^2+y^2_2+y^2_3)+3(h^2+k^2)-6uh-6vk\\

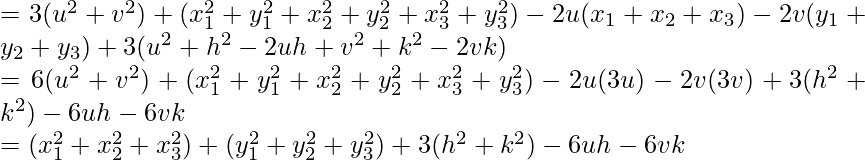
Hence proved

Question 9. If G be the centroid of triangle ABC, prove that AB2 + BC2 + CA2 = 3(GA2 + GB2 + GC2).

Solution:

According to the question 

ABC is a triangle and G be the centroid of this triangle

We have to prove that AB2 + BC2 + CA2 = 3(GA2 + GB2 + GC2)

Proof:

Let us assume that the coordinates of the vertices of ∆ABC be 

A(x1, y1), B(x2, y2), and C(x3, y3) and let G be the centroid of the triangle

Therefore, the coordinates of G will be

(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})

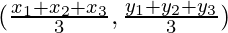
Now L.H.S.= AB2 + BC2 + CA2

= (x1 – x2)2 + (y1 – y2)2 + (x2 – x3)2 + (y2 – y3)2 + (x3 – x1)2 + (y3 – y1)2

=x_1^2+x^2_2-2x_1x_2+x_2^2+x_3^2-2x_2x_3+x_3^2+x_1^2-2x_3x_1+y_1^2+y_2^2-2y_1y_2+y^2_2+y^2_3-2y_2y_3+y_3^2+y_1^2-2y_3y\\ =2(x_1^2+x^2_2+x_3^2)-2(x_1x_2+x_2x_3+x_3x_1)+(y_1^2+y^2_2+y^2_3)-2(y_1y_2+y_2y_3+y_3y_2)\\

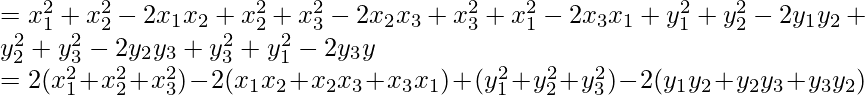
R.H.S = 3[GA2 + GB2 + GC2]

=3[(x_1-\frac{x_1+x_2+x_3}{3})^2+(y_1-\frac{y_1+y_2+y_3}{3})^2+(x_2-\frac{x_1+x_2+x_3}{3})^2+(y2-\frac{y_1+y_2+y_3}{3})^2+(x_3-\frac{x_1+x_2+x_3}{3})^3+(y_3-\frac{y_1+y_2+y_3}{3})]

=3[\frac{(2x_1-x_2-x_3}{3})^2+(\frac{2y_1+y_2-y_3}{3})^2+(\frac{2x_2-x_1-x_3}{3})^2+(\frac{2y_2-y_1-y_3}{3})^2+(\frac{2y_3-x_1-x_2}{3})^2+(\frac{2y_3-y_2-y_3}{3})^2]

=\frac{1}{3}[6x_1^2+6x_2^2-6x_1^2-6x_1x_2-6x_2x_3-6x_3x_1+6y_1^2+6y_2^2+6y_3^2-6y_1y_2-6y_2y_3-6y_3y_1]\\ =2[(x_1^2+x_2^2+x_3^2)-2(x_1x_2+x_2x_3+x_3x_1)+2(y_1^2+y_2^2+y_3^2+y_3^2+y_3^2)-2(y_1y_2+y_2y_3+y_3y_1)]

= L.H.S

Hence proved

Question 10. In the figure, a right triangle BOA is given. C is the mid-point of the hypotenuse AB. Show that it is equidistant from the vertices O, A, and B.

Solution:

In right triangle OAB, 

Co-ordinates of O are (0, 0), A are(2a, 0), and of B are(0, 2b)

C is the midpoint of AB. So, the co-ordinates of C will be

(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})

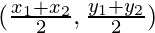
or 

(\frac{2a+0}{2},\frac{0+2b}{2})

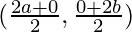
Now CO = 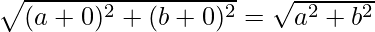\sqrt{(a+0)^2+(b+0)^2}=\sqrt{a^2+b^2}

CA = 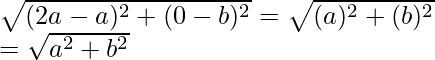\sqrt{(2a-a)^2+(0-b)^2}=\sqrt{(a)^2+(b)^2}\\ =\sqrt{a^2+b^2}

CB = 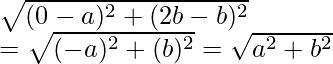\sqrt{(0-a)^2+(2b-b)^2}\\ =\sqrt{(-a)^2+(b)^2}=\sqrt{a^2+b^2}

So, we can conclude that, CO = CA = CB

Hence, C is equidistant to form the vertices O, A and B.

Hence proved


My Personal Notes arrow_drop_up
Related Articles
1. Class 10 RD Sharma Solutions - Chapter 14 Coordinate Geometry - Exercise 14.5 | Set 3
2. Class 11 RD Sharma Solutions - Chapter 28 Introduction to 3D Coordinate Geometry - Exercise 28.1
3. Class 10 RD Sharma Solutions- Chapter 14 Coordinate Geometry - Exercise 14.1
4. Class 11 RD Sharma Solutions - Chapter 28 Introduction to 3D Coordinate Geometry - Exercise 28.2 | Set 1
5. Class 11 RD Sharma Solutions - Chapter 28 Introduction to 3D Coordinate Geometry - Exercise 28.2 | Set 2
6. Class 10 RD Sharma Solutions - Chapter 14 Coordinate Geometry - Exercise 14.2 | Set 1
7. Class 10 RD Sharma Solutions - Chapter 14 Coordinate Geometry - Exercise 14.2 | Set 2
8. Class 11 RD Sharma Solutions - Chapter 28 Introduction to 3D Coordinate Geometry - Exercise 28.3
9. Class 10 RD Sharma Solutions - Chapter 14 Coordinate Geometry - Exercise 14.5 | Set 1
10. Class 10 RD Sharma Solutions - Chapter 14 Coordinate Geometry - Exercise 14.5 | Set 2
Previous
Class 10 RD Sharma Solutions - Chapter 14 Coordinate Geometry - Exercise 14.3 | Set 3
Next
Class 10 RD Sharma Solutions - Chapter 14 Coordinate Geometry - Exercise 14.5 | Set 1
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
ysachin2314
@ysachin2314
Vote for difficulty
Improved By :
Article Tags :
Report Issue
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox

Start Your Coding Journey Now!