As a Part of Society, communication with people around is very common, and not all communications include facts. Facts are the Universal truth that we all know are true and exist but what if someone says “It may Rain Today” Does this consider to be a fact? No, because neither it is a universal truth nor there is a certainty of that event to occur.
There are some statements given in a list below, let’s take a closer look at them:
- India will probably win today.
- Maybe Prime Minister will make an announcement tonight.
- There may be some chances that famous musician John Mayer might come on tour in India.
- There is a 50-50 chance of Barcelona beating Real Madrid today.
Notice that all these statements have the words like “probably”, “chances”, etc used in them. These statements are not certain, there is a chance of these things happening, but it is not necessary that these things will happen. So this uncertainty that is present in these statements is captured by “Probability” in mathematical terms. Let’s define probability in formal terms.
Probability
Probability is an experimental approach to the game of chances we come across every day in our lives. It is a way to describe these “chances” in a mathematical way and then analyze it. It allows us to measure the chances of something occurring.
The concept of probability was developed by famous philosopher and mathematician Blaise Pascal in the 17th century.
Let’s do an experiment,
Suppose we have a coin, we toss it a number of times and then collect the data about heads and tails. We will perform this experiment multiple times and record the data in a table.
| Total Number of Times Coin Tosses | Number of Heads | Number of Tails |
| 5 | 2 | 3 |
| 10 | 7 | 3 |
| 15 | 9 | 6 |
| 20 | 9 | 11 |
Let’s calculate the values of two fractions given below,
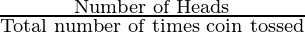
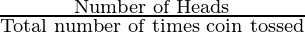
Now if we keep on calculating these values, we will notice that the values start converging towards 0.5 as the number of experiments trials increases.
Trial
A trial is an action that results in one or more outcomes
In the given experiment, tossing a coin is a trial.
Event
An event is an outcome of the trial
Getting a head or a tail after tossing the coin can be considered an event in our experiment. Now let’s define probability.
Sample Space
It is the set of all the possible outcomes
Since sample space, consists of all the possible outcomes. In our case, the number of heads can vary from 0 to the number of times the coin is tossed.
{0, 1, 2, 3, …..n}
Probability
It is a value that denotes the chances of occurrence of some event.
Let “n” be the total number of trials, and E be an event. The probability of occurrence of that event is,
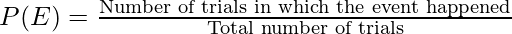
Notice that by its definition, the numerator will always be less than or equal to the denominator. So,
P(E) ≤ 1
Question: Based on the experiment above, let us say a coin was tossed 20 times, and we obtained 15 heads and 5 tails. Find the probability of getting a head and a tail when this coin is tossed again.
Solution:
We know that the coin was tossed 20 times, suppose we want to calculate the probability for heads first.
Probability for Heads:
So the event that we will look for is getting head, this happened 15 times when the coin was tossed 20 times.
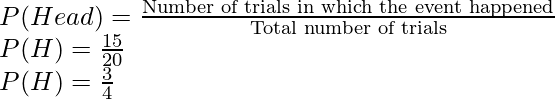
Probability for Tails:
So the event that we will look for is getting a head, this happened 5 times when the coin was tossed 20 times.
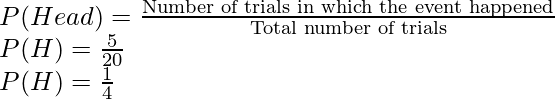
Notice that in the previous example, the probability of head and probability of tails when summed up, give us 1.
Probability with Venn Diagrams
Before introducing Venn diagrams, we need to take a look at the term “Mutually Exclusive”.
Mutually Exclusive: Let’s say there are two events A and B in a trial. If both of them cannot occur simultaneously, then both events are mutually exclusive.
For example: In the coin-tossing experiment, both heads and tails together are not possible. So they are mutually exclusive events in nature.
Another example,
Let’s say a die was rolled, event A is rolling of an odd number and event B is rolling of the number 3. Now, when 3 comes out of dice, both events A and B happen simultaneously. Thus, they are not mutually exclusive.
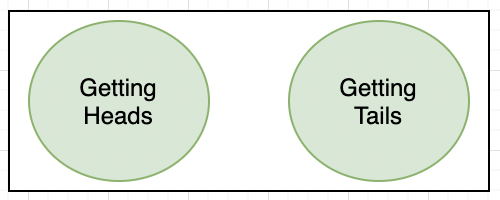
The diagrams below represent the Venn Diagram for the coin toss experiment we did above. Since both events are mutually exclusive, these circles do not intersect.
For the example of a die roll, let’s make a Venn diagram for event A and event B. Notice that the outcomes 1, 5, and 3 are in one circle which denotes event A. 3 is common to both the events, and thus it lies in the intersection. 4 and 6 do not come in any event, and thus they lie outside into the sample space.

These events are not mutually exclusive, thus the diagrams intersect.
Adding Probabilities
In the first example, we saw that the probability of head and the probability of tails added up to 1. This gives rise to another rule of probability.
For mutually exclusive events. The Sum of all the probabilities of all the events in an experiment is always 1. For example:
If a trial has three possible outcomes, A, B and C.
P(A) + P(B) + P(C) = 1
Sometimes we have only one outcome in which we are interested. Let’s say 8 teams are participating in the cricket World Cup. We are interested in finding the probability of winning the world cup for India. We are not interested in finding out the probability for every other team. So we will formulate the problem in the following way,
Let’s say event A denotes India winning the world cup. So, another event B denotes India not winning the world cup.
P(A) + P(B) = 1
P(A) = 1 – P(B)
Such events are called elementary events.
Rules for Adding Probabilities
Suppose there are two events A and B, based on the fact whether both the events are Mutually Exclusive or not, Two different Rules are described,
Rule 1: When the events are Mutually Exclusive
When the events are mutually exclusive, the probability of the events occurring is the sum of both events.
P(A∪ B) = P(A) + P(B)
Rule 2: When the events are not mutually exclusive
There is always some overlapping between two events which are non-mutually exclusive, Therefore, the Probability of the events will become,
P(A∪ B)= P(A) + P(B) – P(A∩ B)
Let’s see some problems with these concepts.
Sample Problems
Question 1: Let’s say a die was rolled. Answer the following questions:
- What is the probability of getting a number greater than 4.
- What is the probability of getting an even number.
Solution:
When a die is rolled, there are six possible outcomes.
1, 2, 3, 4, 5 and 6
Probability of getting a number greater than 4:
Number of favorable outcomes = 2
Total number of outcomes = 6
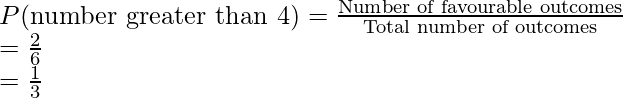
Probability of getting an even number:
Number of favorable outcomes = 3
Total number of outcomes = 6
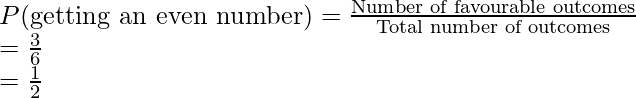
Question 2: Let’s say a card was drawn from a well-shuffled deck of cards. Find the probability of getting a Queen on one draw.
Solution:
We know that a deck has 52 cards. So there are total 52 outcomes that are possible if a card is drawn. We also know that there are four queens in the deck. These are our favorable outcomes.
So,
Total number of outcomes = 52
Total number of favorable outcomes = 4
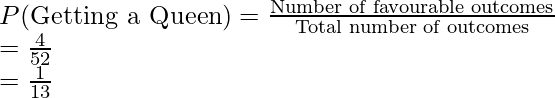
Question 3: A bag contains 3 white balls, 4 black balls, and 2 green balls. A ball is drawn with replacement. Find the probability of getting:
- A White Ball
- A Black Ball
- A Green Ball
Solution:
There are a total of 3 + 4 + 2 = 9 balls.
1. Probability of getting a white ball
Total number of balls = 9,
Favorable outcomes = 3
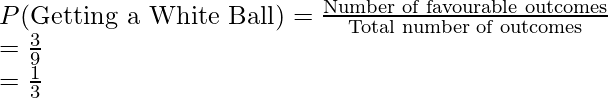
2. Probability of getting a Black ball
Total number of balls = 9,
Favorable outcomes = 4
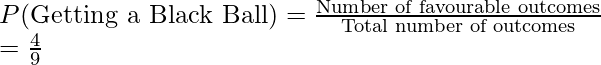
3. Probability of getting a Black ball
Total number of balls = 9,
Favorable outcomes = 2
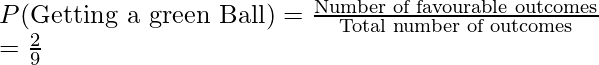
Question 4: A satellite from space came crashing down on earth. The figure below denotes the area in which ISRO suspects the satellite crashed. Find the probability that it crashed in the lake.

Solution:
In this we don’t know the number of outcomes. This is a continuous case, that is plane can crash anywhere in the area.
So, total area of the region = 10 × 5 = 50 Km2
Total area of the lake = 5 × 3 = 15 Km2
Now we can use these areas to calculate the probability.
Total Number of possible outcomes(area in this case) = 50 Km2
Total number of favorable outcomes (area of the lake in this case) = 5 × 3 = 15 Km2
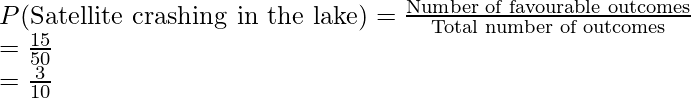
Thus, the probability of satellite crashing in the lake is 0.3.
Question 5: Let’s say we have a well-shuffled deck. We draw two cards, find the probability of getting either King or a Queen.
Solution:
Let’s say drawing a king represents an event A while drawing a queen represents an event B. We are asked for the probability for getting either King or Queen. We will use law of adding probabilities here,
Probability (King or Queen) = Probability (King) + Probability (Queen)
We know that there are 4 Kings and 4 Queens in the deck.
P(King) = 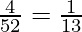
P(Queen) = 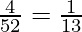
Thus,
Probability (King or Queen) = 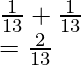
Question 6: We have an urn that contains three black balls, two blue balls, and three white balls. Find the probability of getting one black, one blue, and one white ball if we draw three times with replacement.
Solution:
We have a total of eight balls.
P(getting a black ball) = 
P(getting a blue ball) = 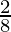
P(getting a white ball) = 
We will find out this probability with law of addition.
So the total probability of getting all three colors = P(Black) + P(Blue) + P(White)
= 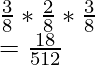
Notice that the probability sums up to one. This is in accordance with laws of probability.
Question 7: Union Budget is going to be announced by the government this week. The probability that it will be announced on a day is given,
| Day | Probability |
| Monday |  [Tex]\frac{1}{7}[/Tex] [Tex]\frac{1}{7}[/Tex] |
| Tuesday |  [Tex]\frac{3}{7}[/Tex] [Tex]\frac{3}{7}[/Tex] |
| Wednesday |  [Tex]\frac{1}{7}[/Tex] [Tex]\frac{1}{7}[/Tex] |
| Thursday |  [Tex]\frac{1}{7}[/Tex] [Tex]\frac{1}{7}[/Tex] |
| Friday |  [Tex]\frac{1}{7}[/Tex] [Tex]\frac{1}{7}[/Tex] |
Find the probability of the budget getting announced between Monday to Wednesday.
Solution:
We need to use the probability addition law,
P(Monday to Wednesday) = P(Monday) + P(Tuesday) + P(Wednesday)
P(Monday) = 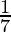
P(Tuesday) = 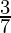
P(Wednesday) = 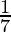
P(Monday to Wednesday) = P(Monday) + P(Tuesday) + P(Wednesday)
= 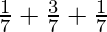
= 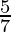
Question 8: In a class of 90 students, 50 took Math, 25 took Physics, 30 took both Math and Physics. Find the number of students who have taken either math or Physics.
Solution:
Since the events of choosing math and physics are non-mutually exclusive, the second rule of addition will be applied here,
P(Math ∪ Physics)= P(Math) + P(Physics) – P(Math ∩ Physics)
P(Math) = 50
P(physics) = 25
P(Math ∩ Physics)= 30
P(Math ∪ Physics)= 50+ 25 – 30
P(Math ∪ Physics)= 30 students.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...