Frustum of a cone is a special shape that is formed when we cut the cone with a plane parallel to its base. The cone is a three-dimensional shape having a circular base and a vertex. So the frustum of a cone is a solid volume that is formed by removing a part of the cone with a plane parallel to circular base. The frustum is not only defined for cones but can be also defined for the different types of pyramids (square pyramid, triangular pyramid, etc.).
Some of the common shapes of a frustum of cone which we discover in our daily life are buckets, lamp shade, and others. Let us learn more about the frustum of cones in this article.
What is Frustum of Cone?
Frustum is a Latin word, which means pieces, therefore frustum of cone is a solid piece of the cone. When a right circular cone is cut by a plane parallel to the base of the cone the shape so obtained is called frustum of the cone. The figure given below shows us how a plane cuts the cone parallel to its base to form the frustum of the cone.

Now, the frustum of the cone is easily defined as,
If a right circular cone is cut off by a plane parallel to it’s base, the shape of the portion between the cutting plane and the base plane is called frustum of cone.
Net of Frustum of Cone
If a three-dimensional (3D) shape is cut open and made a two-dimensional shape the shape so obtained is called the net. One can assume that when the net of the figure is folded properly in a correct manner it forms the desired 3D shape. The image given below shows the net of the frustum of the cone.
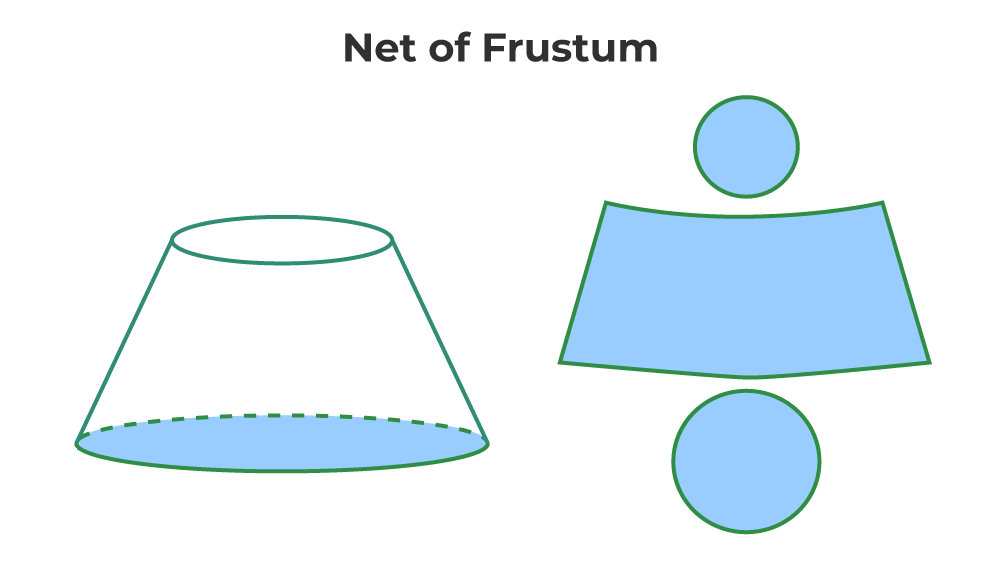
Properties of Frustum of Cone
Properties of a Frustum of a cone are very similar to the cone, some of the important properties of frustum of cone are,
- Base of the cone the original cone is contained in the frustum of a cone but its vertex is not contained in the frustum.
- Formulas of frustum of a cone are dependent on its height and two radii (corresponding to the top and bottom bases).
- Height of the frustum of the cone is the perpendicular distance between the centers of its two bases.
Formulas of Frustum of Cone
Frustum of Cone is such a shape that is frequently seen in our daily life, for example, table lamps, buckets, etc. The important formulas for the frustum of a cone are,
- Volume of Frustum of Cone
- Surface Area of Frustum of Cone
Let’s learn about these formulas in detail below,
Volume of Frustum of Cone
Frustum of cone is a sliced part of a cone, where a small cone is removed from the larger cone. Therefore, to calculate the volume of the frustum of cone, one just needs to calculate the difference between the volume of the larger and smaller cone.
.png)
Let’s assume,
- Total height of the cone is to be H + h
- Total slant height to be l’ + L
- The radius of a complete cone is r
- The radius of the sliced cone is r’
Since the volume of the cone is given as V = 1/3πr2h
Volume of complete cone V1 = 1/3πr2(H+h)
Volume of smaller cone V2 =1/3πr’2(h)
Now the volume of the frustum of cone (V) can be calculated using the formula,
V = V1 – V2
V = 1/3πr2(H+h) – 1/3πr’2(h)
V= 1/3π[r2(H+h) – r’2(h)]…(1)
Using the property of similarity of the triangles of △OCD and △OAB, one can write,
r / (H + h) = r’ / h
r / r’ = (H + h) / h
H + h = hr / r’
Substitute this value of (H+h) in equation (1), and simplify,
V = 1/3π[r2(rh / r’) – r’2(h)}
= 1/3π[{hr3 – hr’3} / r’]…(2)
Using the similar triangle’s property again in △OCD and △OAB, we will find out the value of h
r / (H + h) = r’ / h
r / r’ = (H + h) / h
rh = (H + h)r’
rh = Hr’ + hr’
(r -r’)h = Hr’
h = Hr’ / (r -r’)
Substituting these values in equation (2),
V = 1/3π[{r3h – r3h} / r’]
= 1/3π[{r3 – r’3}h / r’]
= 1/3π[{r3 – r’3}{Hr’ / (r – r’)} / r’]
= 1/3πH(r2 + r’2 +rr’)
Thus,
Volume of the frustum of cone = 1/3 πH(r2 + r’2 + rr’)
Surface Area of Frustum of Cone
The surface area of frustum of cone can be calculated by the difference between the surface area of the complete cone and the smaller cone (removed from the complete cone). The surface area of the frustum of cone can be calculated using the below diagram, where one needs to sum up the surface areas of the curved surfaces, and the surface areas of the top and bottom surfaces of the frustum of cone.

Similar to the Volume of the frustum of cone, the curved surface area will be also equal to the difference between the surface areas of the bigger cone and the smaller cone.
In the figure given above, triangles OAB and OCD are similar. Therefore, using the similarity criteria, one can write,
l’ / l = r’ / r…(1)
Since, l’ = l – L, therefore, from equation (1),
(l – L) / l = r’ / r
After cross-multiplication,
lr – Lr = lr’
l(r – r’) = Lr
l = Lr / (r – r’)…(2)
The curved surface area of a complete cone = πrl
The curved surface area of the smaller cone = πr’l’
Difference between the curved surface areas of complete cone and smaller cone = π (rl – r’l’)
Thus, the curved surface area (CSA) of the frustum of cone = πl (r – r’l’/l)
Use equation (1) to substitute the value of l’/l in the above equation, and simplify,
CSA of the frustum of cone = πl (r – r’×r’/r) = πl (r2 – r’2)/r
Now, substitute the value of l from equation (2), and simplify,
CSA of the frustum of cone = πlr/(r – r’)× (r2 – r’2)/r = πl (r + r’)
Thus, one can write,
Curved surface area of frustum of cone = πl (r + r’)
Now, let’s calculate the surface area of the top and bottom bases of the frustum of the cone, such that,
The surface area of the top base of the frustum of cone having a radius r’ = πr’2
The surface area of the bottom base of the frustum of cone having a radius r = πr2
So,
Total surface area of the frustum of cone = Curved surface area of the frustum of cone + surface area of the top base + surface area of the bottom base
Therefore,
The total surface area of the frustum of cone = πl (r + r’) + πr’2 + πr2 = πl (r + r’) + π (r2 + r’2)
Thus, the total surface area of the frustum of cone is = πl (r + r’) + π (r2 + r’2)
This formula can be also written as,
The total surface area of the frustum of cone is = πl (r2 – r’2)/r + π (r2 + r’2)
So, one can write,
Total surface area of frustum of cone = πl(r + r’) + π (r2 + r’2)
or
Total surface area of frustum of cone = πl (r2 – r’2)/r + π (r2 + r’2)
Note that, l is the slant height of the smaller cone that can be given as
L = √ [H2 + (r – r’)2]
Read, More
Solved Examples on Frustum of Cone
Example 1: Find out the Volume of a frustum of a cone that is 15 cm high and the radii for both the bases are 5 cm and 8 cm.
Solution:
Using the formula studied above, one can write,
V = 1/3 πH(r2 + r’2 + rr’)
Given,
H = 15 cm
r’= 5 cm
r = 8 cm
V = 1/3 π15(82 + 52 + 40)
V = 5π(129)
V = 645π cm3
Example 2: Find out the surface area and total surface area of a frustum of a cone which is 10 cm high and the radii for both the bases are 4 cm and 8 cm.
Solution:
We know the formula for surface area and total surface area of the frustum. We need to plug in the required values.
Curved Surface area of the frustum = πl(r+r’)
where,
L = √ [H2 + (R – r)2]
Given,
H = 10 cm
r = 4 cm
R = 8 cm
Calculating the value of L,
L = √ [102 + (8 – 4)2]
= √(100+16) = √(116)
Curved Surface Area of Frustum = πL(R+r)
= π√(116)×(8+4)
= 48π√(29)
Total Surface Area = Curved Surface Area of Frustum + Area of Both Bases
= 48π√(29) + π(8)2 + π(4)2
= 48π√(29) + 64π + 16π
= 48π√(29) + 80π cm2
Example 3: Let’s say we have an open metal bucket whose height is 50cm and the radii of the bases are 10cm and 20cm. Find the area of the metallic sheet used to make the bucket.
Solution:
Bucket is in the form of frustum which closed from the bottom. We need to calculate the total surface area of this frustum.
Given
H = 50 cm
r ‘= 10 cm
r = 20 cm
Curved Surface Area of Frustum = πL(R+r)
L = √ [H2 + (r – r’)2]
L = √ [502 + (20 – 10)2]
= √(2500+100) = √(2600)
= √100(26) = 10√(26)
Curved Surface Area of Frustum = πL(R+r)
= π10√(26)×(20+10)
= 300π√(26)
Total Surface Area = Curved Surface Area of Frustum + Area of Both Bases
= 300π√(26) + π(20)2 + π(10)2
= 300π√(26) + 400π + 100π
= (300π√(26) + 500π) cm2
Example 4: Find out the expression of the volume for a frustum if its height is 6y, and its radii are y and 2y respectively.
Solution:
Using the formula studied above,
V = 1/3 πH(r2 + r’2 + rr’)
Given,
H = 6y
r’= y
r = 2y
V = 1/3 π6[(2y)2 + (y)2 + (y)(2y)]
V = 2πy(7y2)
V = 14πy3 unit3
FAQs on Frustum of Cone
Question 1: What is the Frustum of a Cone?
Answer:
When we cut a cone in such a way that the plane of cutting is parallel to the base of the cone. The resultant figure so obtained is called the Frustum of the Cone.
Question 2: What are the Frustum of Cone Formulas?
Answer:
The formulas of the frustum of a cone are discussed below. Let’s take a frustum of base radius ‘R’ and top radius ‘r’, height ‘H’, and slant height then,
- Volume of frustum of a cone (V) = 1/3πH(r2 + rr’ + r’2)
- Total surface area of frustum of a cone = πl (r + r’) + π (r’2 + r2).
Question 3: What is the CSA of a frustum?
Answer:
The curved surface area of the frustum of a cone is calculated using the formula,
CSA = πl (r + r’)
where,
r’ is the radius of the upper circle of frustum
r is the radius base
l is the slant height
Question 4: What is the Surface Area of Frustum of Cone?
Answer:
The surface area of the frustum of a cone is calculated using the formula,
- CSA of frustum of cone = πl [ (r2 – r’2) / r’ ]
- TSA of frustum of cone = π (r2 + r’2) + πl [ (r2 – r’2) / r’]
Question 5: What is the Volume of the Frustum of Cone?
Answer:
The volume of the frustum of a cone is calculated using the formula,
- V = 1/3πh[ (r3 – r’3) / r’]
- V = 1/3πH(r2 + rr’ + r’2)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...