Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.6
Last Updated :
03 Apr, 2024
This exercise has been deleted as per new NCERT Syllabus
Question 1. In Fig., PS is the bisector of ∠QPR of ΔPQR. Prove that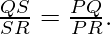

Solution:
Given: PS is angle bisector of ∠QPR.
To prove: 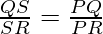
Construction: Draw RT∥ST to cut OP provided at T.
Proof: since PS∥TR and PR cuts them, hence we have,
∠1 = ∠3 ——[alternate interior angle] 1
∠1 = ∠4 ——[corresponding angle] 2
But ∠1 = ∠2 [given]
From 1 and 2
∴∠3=∠4
In ∆PTR,
PT = PR [sides opposite to equal angle are equal] 3
Now In ∆QRT, we have
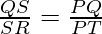 ———-[by B.P.T]
———-[by B.P.T]
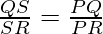 ———[from 3]
———[from 3]
Question 2. In Fig., D is a point on hypotenuse AC of ΔABC, such that BD ⊥ AC, DM ⊥ BC and
DN ⊥ AB. Prove that:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN

Solution:
Given: BD ⊥ AC, DM ⊥ BC and DN ⊥ AB
To prove:
(i) DM2 = DN.MC
(ii) DN2 = DM.AN
Proof: we have AB⊥BC and DM⊥BC
So, AB || DM
Similarly, we have CB⊥AB and DN ⊥ AB
Therefore, CB || DN
Hence, BMD DN is a triangle
∴BM=DN or DM=ND
In ∆BMD,
∠1+ ∠2+ ∠DMB=180 ———–[angle sum property of triangle]
∠1+ ∠2+90=180
∠1+ ∠2=180-90
∠1+ ∠2=90 ——————-1
Similarly, in ∆DMC,
∠3+ ∠4=90° _______2
∴ from 1 and 2
∠1+ ∠2=∠2+ ∠3
∠1=∠3
From 2 and 3
∠3+ ∠4=∠2+ ∠3
∠4=∠2
Now in ∆BMD and ∆DMC,
∠1=∠3
∠2=∠4
∴∆BMD~∆DMC ——-(AA similarity criteria)
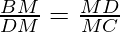
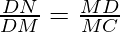
DM2=DN*MC
II) proceeding as in (i), we can prove that ∆BND~∆DNA
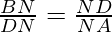
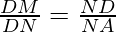 [BN=NA]
[BN=NA]
DN2 = MN*MC
Question 3. In Fig., ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2 BC.BD.

Given: In ∆ABC, ∠ABC > 90° and AD⊥CB provided.
To prove: (AC)2= AB2+BC2+ 2 BC.BD
Proof: In ∆ADB by Pythagoras theorem,
AC2=AD2+AB2
(AC)2= (AD)2+(DB)2 ———1
In ∆ADC by Pythagoras theorem,
(AC)2= (AD)2+(DC)2 ———2
AC2= AD2+DB2 ———1
AC2= AD2+(DB)2+2*DB*BC
AC2= AD2+(DB)2+BC2+2*DB*BC
Question 4. In Figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 – 2BC.BD.

Solution:
Given: In ∆ABC, ∠ABC < 90° and AD ⊥ BC.
To prove: AC2 = AB2 + BC2 – 2*BC.BD
Proof: In triangle ADB, by Pythagoras theorem
AB2=AD2 +BD2 ———1
In triangle ADC, by Pythagoras theorem
AC2=AD2+DC2 ———2
AC2=AD2+ BC2 +BD2
AC2=AD2+ BC2 +BD2 – 2*BC*BD
AC2=AB2+ BD2+BC2 – 2*BC*BD
AC2 = AB2 + BC2 – 2BC.BD
Question 5. In Fig., AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
(i) AC2 = AD2 + BC.DM + (BC/2)2
(ii) AB2 = AD2 – BC.DM + (BC/2)2
(iii) AC2 + AB2 = 2 AD2 + 1/2 BC2

Given: In ∆ABC, AD is a median, AM ⊥ BC.
Prove that:
(i) AC2 = AD2 + BC.DM + (BC/2)2
(ii) AB2 = AD2 – BC.DM + (BC/2)2
(iii) AC2 + AB2 = 2 AD2 + 1/2 BC2
Proof: i) In obtuse ∆ADC,∠D>90°
AC2 = AD2 + DC2+2DC.DM
AC2 = AD2 +(BC/2)2+2(BC/2).DM
AC2 = AD2 +(BC/2)2+BC.DM
Or AC2 = AD2 +BC.DM+(BC/2)2
II)In acute triangle ABD,
∠D>90°
AB2 = AD2 + BD2+2BD.DM
AB2 = AD2 +(BC/2)2-2(BC/2).DM
AB2 = AD2 +(BC/2)2-BC.DM
Or
AB2 = AD2 -BC.DM +(BC/2)2
iii) Adding i and ii
AC2 +AB2 =AD2+BC.DM+(BC/2)2 +AD2 -BC.DM +(BC/2)2
= 2 AD2+BC/42 +BC/42
= 2AD2+1/2.BC/42
= 2AD2+ BC2
Question 6. Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.

Solution:
Given: ||gm ABCD and diagonals BD and AC
To prove: AB2+BC2+CD2+AD2=AC2+BD2
Proof: Diagonals of ||gm bisects each other at midpoint
Solution: In ∆ABC, BO is median
∴AB2+BC2=2BO2+1/2AC2 ———1
In ∆ADC, DO is median
∴AD2+DC2 = 2DO2+1/2AC2 ———2
Adding 1 and 2
AB2+BC2+AD2+DC2=2BO2+1/2AC2+2DO2+1/2AC2
=2.(1/2.BD)2 +1/2AC2+2(1/2BD)2+1/2AC2
=2.BD/42 +1/4AC2+2.BD/42+1/2AC2
=BD2/2+1/2AC2 +BD2/2+1/2AC2
=BD2+AC2
Question 7. In Fig., two chords AB and CD intersect each other at the point P. Prove that :
(i) Δ APC ~ Δ DPB
(ii) AP.PB = CP.DP

Solution:
Given: chords AB and CD intersect each other at the point P.
To prove: (i) Δ APC ~ Δ DPB (ii) AP.PB = CP.DP
Proof: In ∆ABC and ∆DPB,
∠1=∠2 ——-[vertically opposite angle]
∠A=∠D ——-[angle in the same segment of circle are equal]
i) ∴∆APC~∆DPB (AA similarity criteria)
ii) 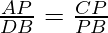
AP*PB=CP*DP
Question 8. In Fig., two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) Δ PAC ~ Δ PDB
(ii) PA.PB = PC.PD

Solution:
i) In ∆PAC and ∆PDB,
∠P=∠P ———[common]
∠1+∠2=180° ——–[linear pair angle]
∠2=180°+∠1
∠2+∠3=180° ——[sum of opposite angle of a cyclic quadrilateral is 180°]
∠3=180°-180°+∠1
∠3=∠1 ————2
∠1=∠3 ———–[form 2]
∴∆APC~∆PDB ———[AA similarity criteria]
ii) 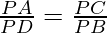
PA*PD = PC*PB
Question 9. In Fig., D is a point on side BC of ΔABC such that 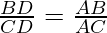 . Prove that AD is the bisector of ∠BAC.
. Prove that AD is the bisector of ∠BAC.

Solution:
Construction: Produce BA to E such that AE=AC join CE.
Proof: In ∆AEC,
Since AE=AC
∴∠1=∠2 ——[Angle opposite to equal sides of ∆are=]
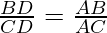
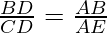 ———–(BY CONSTRUCTION)
———–(BY CONSTRUCTION)
By converse of BPT
AD||EC
And AC is a transversal then
∠3=∠1 ——-[corresponding angles]
∠4=∠2 ——-[alternate interior angles]
But ∠1=∠2 ——–[by construction]
∴AD bisects ∠BAC internally
Question 10. Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig.)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Solution:
In ∆ABC,
AC is string
By Pythagoras theorem,
AC2=AB2+BC2
AC2=AB2+BC2
AC2=(1.8)2+(2.4)2
(AC)2=3.24+5.76
AC=√9
AC=3m
∴Length of string she have out=3m
=5cm/sec*12sec
=60cm
=60/100 =0.6m
AP=AC-0.6
=3-06
=2.4 m
Now in ∆ABP by Pythagoras theorem,
(AP)2=(AB)2+(PB)2
(2.4)2=(1.8)2+(PB)2
5.76=3.24 + (PB)2
5.76=3.24 + (PB)2
2.52=(PB)2
√2.52= PB
1.59=PB
PD=PB+BD
PD=1.59+1.2
PD=2.79m ———(approx)
Hence, the horizontal distance of the fly from nazima of the 12 sec in 2.79m.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...