Construction of Similar Triangles
Last Updated :
19 Apr, 2021
The basic construction techniques allow constructing perpendicular bisectors, angle bisectors, and so on. These basic techniques can be used for more complex constructions. These constructions are very essential for the designers who design buildings, roads, machines .. Etc. So, these techniques are very handy in real life. As the name suggests similar triangles are those triangles that are similar in appearance, angles, and the ratio of their sides. But if a triangle is given and is asked to make a similar triangle, how will it be done? Is there a need to construct the whole triangle again? For this purpose, some construction techniques were developed to simplify the process.
Similar Triangles
Similar triangles are triangles that are not congruent, but they are similar in nature. There are a few conditions that must be satisfied when two triangles are similar.
Let’s say we have two triangles which are similar ΔABC and ΔXYZ. The two triangles must follow two conditions:
1. The corresponding angles of the triangles must be equal
∠A = ∠X, ∠B = ∠ Y and ∠ C = ∠ Z
2. The corresponding sides of both the triangles must be in same ratio.
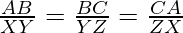

Construction of Similar Triangles
This construction of similar triangles involves two cases:
- The triangle to be constructed is larger than the original triangle
- The triangle to be constructed is smaller than the original triangle.
Scale Ratio: We define scale ratio as the ratio of the sides of the triangle constructed with the sides of the original triangle.
Sample Constructions
Let’s see the construction in both cases through some examples,
Question 1: Construct a triangle similar to triangle ΔPQR with the scale ratio = 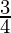
Solution:
We know that the scale ratio must be 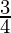 , that is the sides of the new triangle must be
, that is the sides of the new triangle must be 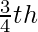 , of the sides of the original triangle.
, of the sides of the original triangle.
Steps of Construction:
Step 1. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P.

Step 2. On the ray QX, make four points Q1, Q2, Q3 and Q4 on QX in such a way that QQ1 = QQ2 = QQ3 = QQ4. Now on this ray locate the 4th point(whichever is greater in the fraction 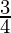

Step 3. Now join Q4R and draw a line from Q3 parallel to Q4R and let it intersect QR at R’.

Step 4. Draw a line from R’ which is parallel to the line RP. Let it intersect PQ and P’

ΔPQ’R’ is our required triangle.
Question 2: Construct a triangle similar to triangle ΔPQR with the scale ratio = 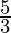 .
.
Solution:
This is an example of the second case, scale ratio is given by 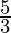 . That is the sides of the new triangle must be
. That is the sides of the new triangle must be 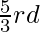 , of the sides of the original triangle. The steps in this case are similar to the above case, but with some minor modification.
, of the sides of the original triangle. The steps in this case are similar to the above case, but with some minor modification.
Steps for Construction:
Step 1. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P.

Step 2. On the ray QX, make four points Q1, Q2, Q3, Q4, Q5on QX in such a way that QQ1 = QQ2 = QQ3 = QQ4 = QQ5. Now on this ray locate the 5th point whichever is greater in the fraction 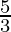

Step 3. Join the 3rd point with R and draw a line that is parallel to Q3R through the 5th point, let it intersect the extended line QR at R’.

Step 4. Now, we need to draw the line through R’ which parallel to PR, it should intersect the extended line of PQ and P’.

ΔP’QR’ is our required triangle.
Question 3: Draw a triangle of sides 10cm, 11cm, and 8cm. Then draw a triangle that is similar to it with a scale ratio of 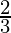 .
.
Solution:
Steps of the construction:
Step 1. Draw a triangle of 10cm, 11cm and 8cm.
We know that the scale ratio must be 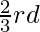 , that is the sides of the new triangle must be
, that is the sides of the new triangle must be 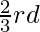 , of the sides of the original triangle.
, of the sides of the original triangle.
Step 2. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P.
Step 2. On the ray QX, make three points Q1, Q2, Q3 on QX in such a way that QQ1 = QQ2 = QQ3. Now on this ray locate the 2nd point(whichever is greater in the fraction 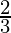
Step 3. Now join Q3R and draw a line from Q2 parallel to Q3R and let it intersect QR at R’.
Step 4. Draw a line from R’ which is parallel to the line RP. Let it intersect PQ and P’

ΔPQ’R’ is our required triangle.
Question 4: In the original triangle of the previous question. Draw a triangle that is similar to it with a scale ratio of 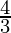 .
.
Solution:
Steps of the construction:
Step 1. Draw a triangle of 10cm, 11cm and 8cm.
We know that the scale ratio must be 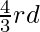 , that is the sides of the new triangle must be
, that is the sides of the new triangle must be 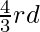 , of the sides of the original triangle.
, of the sides of the original triangle.
Step 2. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P.
Step 3. On the ray QX, make four points Q1, Q2, Q3, Q4, Q5on QX in such a way that QQ1 = QQ2 = QQ3 = QQ4 = QQ5. Now on this ray locate the 5th point whichever is greater in the fraction 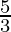
Step 4. Join the 3rd point with R and draw a line that is parallel to Q3R through the 5th point, let it intersect the extended line QR at R’.
Step 5. Now, we need to draw the line through R’ which parallel to PR, it should intersect the extended line of PQ and P’.

ΔP’QR’ is our required triangle.
Question 5: Draw a triangle of sides 4cm, 5cm, and 6cm. Then draw a triangle that is similar to it with a scale ratio of 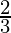 .
.
Solution:
Steps of the construction:
Step 1. Draw a triangle of 4cm, 5cm and 6cm.
We know that the scale ratio must be 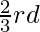 , that is the sides of the new triangle must be
, that is the sides of the new triangle must be 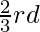 , of the sides of the original triangle.
, of the sides of the original triangle.
Step 2. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P.
Step 2. On the ray QX, make three points Q1, Q2, Q3 on QX in such a way that QQ1 = QQ2 = QQ3. Now on this ray locate the 2nd point(whichever is greater in the fraction 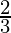
Step 3. Now join Q3R and draw a line from Q2 parallel to Q3R and let it intersect QR at R’.
Step 4. Draw a line from R’ which is parallel to the line RP. Let it intersect PQ and P’.

ΔPQ’R’ is our required triangle.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...