Question 20. The three vertices of a parallelogram are (3, 4), (3, 8), and (9, 8). Find the fourth vertex.
Solution:

Let ABCD be a parallelogram and vertices will be A (3, 4), B (3, 8), C (9, 8)
and the co-ordinates of fourth vertex D be(x, y)
Now AB = 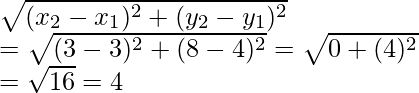
Similarly, BC = 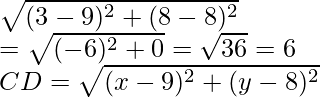
and DA = 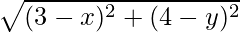
Hence, ABCD is a ||gm
Here, AB = CD and BC = AD
CD = 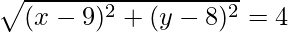
On squaring both sides we get
(x – 9)2 + (y – 8)2 = (4)2
x2 – 18x + 81 + y2 – 16y + 64 = 16
x2 + y2 – 18x – 16y = 16 – 81 – 64
x2 + y2 – 18x – 16y = -129 ………..(i)
Similarly, AD = 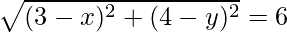
On squaring both sides we get
(3 – x)2 + (4 – y)2 = 26
9 + x2 – 6x + 16 + y2 – 8y = 36
x2 + y2 – 6x – 8y = 36 – 9 – 16
x2 + y2 – 6x – 8y = 11 ………..(ii)
Now on subtracting eq(i) from (ii), we get
12x + 8y = 140
3x + 2y = 35
2y = 35 – 3x
y = (35 – 3x)/2 ………..(iii)
Now substituting the value of y in eq (ii)
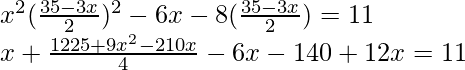
4x2 + 1225 + 9x2 – 210x – 24x – 560 = 44
13x2 – 186 + 621 = 0
13x2 – 117x – 69x + 621 = 0
13x(x – 9) – 69(x – 9) = 0
(x – 9)(13x – 69) = 0
Either x – 9 = 0, then x = 9
or 13x – 69 = 0, then x69/13 which is not possible
So, x = 9
Hence, the vertex will be (9,4)
Question 21. Find a point which is equidistant from the point A (-5, 4) and B (-1, 6). How many such points are there?
Solution:
Let us considered P (h, k) be the point which is equidistant from the points A (-5, 4) and B (-1, 6).
So, PA = PB
Therefore, (PA)2 = (PB)2
Now by distance formula, we get
(-5 – h)2 + (4 – k)2 = (-1 – h)2 + (6 – k)2
25 + h2 + 10h + 16 + k2 – 8k = 1h2 + 2h + 36 + k2 – 12k
25 + 10h + 16 – 8k = 1 + 2h + 36 – 12k
8h + 4k + 41 – 37 = 0
8h + 4k + 4 = 0
2h + k + 1 = 0 …….(i)
Midpoint of AB = ((-5 – 1)/2, (4 + 6)/2) = (-3, 5)
At point (-3, 5), from eq(i)
2h + k = 2(-3) + 6
-6 + 5 = -1
2h + k + 1 = 0
So, the mid-point of AB satisfy the Eq. (i).
Hence, infinite number of points, in fact all points which are solution
of the equation 2h + k + 1 = 0, are equidistant from the point A and B.
Replacing h, k, by x, y in above equation, we have 2x + y + 1 = 0
Question 22. The centre of a circle is (2a, a – 7). Find the values of a if the circle passes through the point (11, -9) and has diameter 10√2 units.
Solution:

According to the question
Distance between the centre C (2a, a – 1) and the point P (11, -9), which lie on the circle = Radius of circle
So, Radius of circle =  …..(i)
…..(i)
Given that, length of diameter = 10√2
Therefore, length of radius = Length of diameter/2
= 10√2/2 = 5√2
Now put this value in eq(i), we get
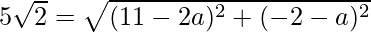
Squaring on both sides, we get
50 = (11 – 2a)2 + (2 + a)2
50 = 121 + 4a2 – 44a + 4 + a2 + 4a
5a2 – 40a + 75 = 0
a2 – 8a + 15 = 0
a2 – 5a – 3a + 15 = 0
a(a – 5) – 3(a – 5) = 0
(a – 5)(a – 3) = 0
So, a = 3, 5
Hence, the required values of a are 5 and 3.
Question 23. Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter’s school and then reaches the office. What is the extra distance travelled by Ayush in reaching the office? (Assume that all distance covered are in straight lines). If the house is situated at (2, 4), bank at (5, 8), school at (13, 14), and office at (13, 26), and coordinates are in kilometers.
Solution:

According to the figure
Distance between two points 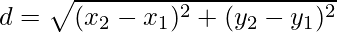
Now, distance between house and bank

Distance between bank and daughter’s
School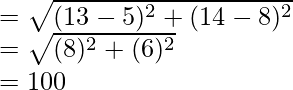
Distance between daughter’s school and office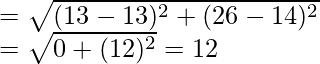
Total distance (house+bank+school+office) travelled = 5 + 10 + 12 = 27 units
Distance between house to offices
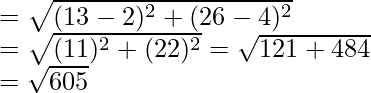 = 24.59 = 24.6km
= 24.59 = 24.6km
So, the extra distance travelled by Ayush in reaching his office = 27 – 24.6 = 2.4km.
Hence, the required extra distance travelled by Ayush is 2.4 km
Question 24. Find the value of k, if the point P (0, 2) is equidistant from (3, k) and (k, 5).
Solution:
Let us considered P (0, 2) is equidistant from A (3, k) and B (k, 5)
PA = PB
=> PA2 = PB2

Therefore, PA2 = (0 – 3)2 + (2 – k)2
= (-3)2 + (2 – k)2
= k2 – 4k + 13
Similarly, PB2 = (k – 0)2 + (5 – 2)2
= k2 + (3)2 = k2 + 9
Therefore, PA = PB
PA2 = PB2
k2 – 4k + 13 = k2 + 9
-4k = 9 – 13
-4k = -4
k = -4/-4 = 1
Hence, K = 1.
Question 25. If (-4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the
(i) interior,
(ii) the exterior of the triangle.
Solution:
Let us considered the third vertex of an equilateral triangle be (x, y).
So, the vertices are A (-4, 3), B (4,3) and C (x, y).
We know that, in equilateral triangle the angle between two
adjacent side is 60 and all three sides are equal.
Therefore, AB = BC = CA
AB2 = BC2 = CA2 …..(i)
Now, taking first two parts
AB2 = BC2
(4 + 4)2 + (3 – 3)2 = (x – 4)2 + (y – 3)2
64 + 0 = x2 + 16 – 8x + y2 + 9 – 6y
x2 + y2 – 8x – 6y = 39 …..(ii)
Now, taking first and third parts.
AB2 = CA2
(4 + 4)2 + (3 – 3)2 = (x – 4)2 + (y – 3)2
64 + 0 = x2 + 16 – 8x + y2 + 9 – 6y
x2 + y2 – 8x – 6y = 39
On subtracting eq(ii) from (iii), we get
x = 0
Now, put the value of x in eq(ii), we get
0 + y2 – 0 – 6y = 39
y2 – 6y – 39 = 0
Therefore, y = 
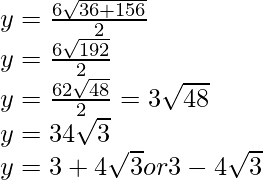
So, the points of third vertex are
(0, 3+√3)or(3 – 4√3)
But it is given that, the origin lies in the interior of the ∆ABC and the x-coordinate of third vertex is zero.
So, y-coordinate of third vertex should be negative.
Hence, the requirement coordinate of third vertex,
C = (0, 3 – 4√3)
Question 26. Show that the points (-3, 2), (-5, -5), (2, -3), and (4, 4) are the vertices of a rhombus. Find the area of this rhombus.
Solution:
Let us considered the co-ordinates of the vertices A, B, C and D of a rhombus are A (-3, 2), B (-5, -5), C (2, -3) and D (4, 4)
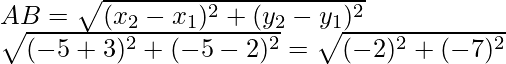
or AB2 = (-2)2 + (-7)2 = 4 + 49 = 53
Similarly, BC2 = (2 + 5)2 + (-3 + 5)2
= (7)2 + (2)2 = 49 + 4 = 53
CD2 = (4 – 2)2 + (4 + 3)2
= (2)2 + (7)2 = 4 + 48 = 53
and DA2 = (-3 – 4)2 + (2 – 4)2
= (-7)2 + (-2)2 = 49 + 4 = 53
Therefore, we see that AB = BC = CD = DA = √53
Now diagonals AC = 
and diagonal BD = 
Therefore, sides are equal but diagonal are not equal
Hence, ABCD is a rhombus
Now we find the area of rhombus = Product of diagonal/2
= (5√2 × 9√2)/2
= 9/2
= 45sq.units
Question 27. Find the coordinates of the circumcenter of the triangle whose vertices are (3, 0), (-1, -6), and (4, -1). Also, find its circumradius.
Solution:

Let us considered ABC is a triangle whose vertices are A (3, 0), B (-1, -6) and C (4, -1)
So, O be the circumcenter of the triangle ABC and so the co-ordinates be (x, y)
Therefore, OA = OB = OC
OA2 = OB2 = OC2
Now OA = 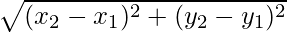
OA2 = (x2 – x1)2 + (y2 – y1)2
= (x – 3)2 + (y – 0)2
= (x – 3)2 + y2
OB2 = (x + 1)2 +(y + 6)2
and OC2 = (x – 4)2 + (y + 1)2
Therefore, OA2 = OB2
(x – 3)2 + y2 = (x + 1)2 + (y + 6)2
x2 – 6x + 9 + y2 = x2 + 2x + 1 + y2 + 12y + 36
-6x – 2x – 12y = 1 + 36 – 9
-8x – 12y = 28
2x + 3y = -7 ……..(i)
Therefore, OB2 = OC2
(x + 1)2 + (y + 6)2 = (x – 4)2 + (y + 1)2
x2 + 2x + 1 + y2 + 12y + 36 = x2 – 8x + 16 + y2 + 2y + 1
2x + 12y + 37 + 8x – 2y = 17
10x + 10y = 17 – 37 = -20
x + y = -2 ……..(ii)
On multiply eq(i) by 1 and (ii) by 2, we get
2x + 3y = -7
2x + 2y = -4
Now, on substituting y = -3, we get
x + y = -2
x – 3 = -2
x = -2 + 3 = 1
Radius = OA = 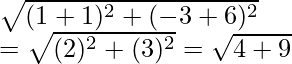 = √13
= √13
Question 28. Find a point on the x-axis which is equidistant from the points (7, 6) and (-3, 4).
Solution:
The required point is on x-axis
Its ordinate will be O
So, the co-ordinates of the required point P (x, 0)
It is given that the point P is equidistant from the points A (7, 6) and B (-3, 4)
Now AP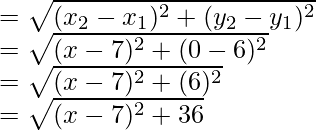
Therefore, AP2 = (x – 7)2 + 36
Similarly, BP2 = (x + 3)2 + (0 – 4)2
= (x + 3)2 + 16
Therefore, AP = BP
AP2 = BP2
Therefore, (x – 7)2 + 36 = (x + 3)2 + 16
x2 – 14x + 49 + 36 = x2 + 6x + 9 + 16
x2 – 14x – x2 – 6x = 25 – 85
-20x = -60
x = -60/-20 = 3
Therefore, the required point will be (3, 0)
Question 29. (i) Show that the points A (5, 6), B (1, 5), C (2, 1), and D (6, 2) are the vertices of a square.
(ii) Prove that the points A (2, 3), B (-2, 2), C (-1, -2), and D (3, -1) are the vertices of a square ABCD.
(iii) Name the type of triangle PQR formed by the point P(√2, √2), Q(- √2, – √2), and R (-√6, √6).
Solution:
(i) Given points are given A (5, 6), B (1, 5), C (2, 1) and D (6, 2)
Now AB2 = (x2 – x1)2 + (y2 – y1)2
= (1 – 5)2 + (5 – 6)2
= (-4)2 + (-1)2 = 16 + 1 = 17
Similarly, BC = (2 – 1)2 + (1 – 5)2
= (1)2 + (-4)2
= 1 + 16 = 17
CD = (6 – 2)2 + (2 – 1)2 + (4)2 + (1)2
= 16 + 1 = 17
and DA = (5 – 6)2 + (6 – 2)2
= (-1)2 + (4)2
= 1 + 16 = 17
Diagonals AC2 = (2 – 5)2 + (1 – 6)2
= (-3)2 + (-5)2
= 9 + 25
=34
and BD2 = (6 – 1)2 + (2 – 5)2
= (5)2 + (-3)2
= 25 + 9 = 34
We conclude that
AB = BC = CD = DA and diagonals AC = BD
Hence, ABCD is a square.
(ii) Given points A(2, 3), B(-2, 2), C(-1, -2) and D(3, -1)

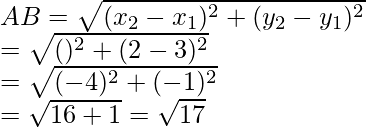
Similarly,
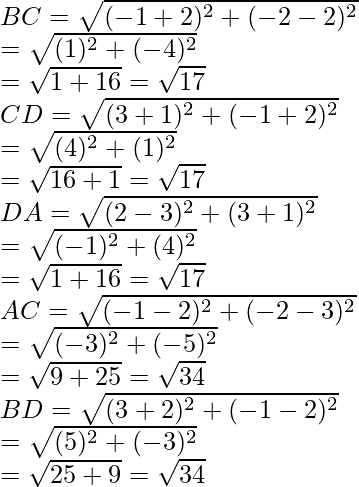
Therefore, AB, BC, CD and DA are equal and diagonals AC and BD are also equal
Hence, ABCD is a square.
(iii) Using distance formula

Since, PQ = PR = RQ = 4, so, the point P, Q, R form an equilateral triangle.
Question 30. Find the point on x-axis which is equidistant from the points (-2, 5) and (2, -3).
Solution:
Let us considered point P lies on x-axis
So, the coordinates of point P be (x, 0)
It is given that P is equidistant from A (-2, 5) and B (2, -3)
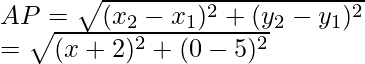
AP2 = (x + 2)2 + (-5)2
= (x + 2)2 + 25
BP2 = (x – 2)2 + (0 + 3)2
= (x – 2)2 + 9
AP = BP
So, AP2 = BP2
(x + 2)2 + 25 = (x – 2)2 + 9
x2 + 4x + 4 + 25 = x2 – 2x + 4 + 9
x2 + 4x – x2 + 4x = 13 – 29
8x = -16
x = -16/8
x = -2
Hence, the co-ordinates of point P are(-2, 0)
Question 31. Find the value of x such that PQ = QR where the co-ordinates of P, Q, and R are (6, -1), (1, 3), and (x, 8) respectively.
Solution:
Given that the co-ordinates of P (6, -1), Q(1, 3), and R(x, 8)
Also, PQ = QR
By using the distance formula
D = 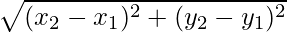
We find the length of PQ and QR
PQ2 = (1 – 6)2 + (3 + 1)2
= (-5)2 + (4)2
= 25 + 16 = 41
QR2 = (x – 1)2 + (8 – 3)2
= (x – 1)2 + (5)2 = (x – 1)2 + 25
It is given that PQ = QR
So PQ2 = QR2
41 = (x – 1)2 + 25
(x – 1)2 = 41 – 25 = 16 = (±4)2
x – 1 = ±4
If x – 1 = 4, then x = 1 + 4 = 5
If x – 1 = -4 then x = -4 + 1 = -3
Hence, the value of x = 5, -3
Question 32. Prove that the points (0, 0), (5, 5), and (-5, 5) are the vertices of a right isosceles triangle.
Solution:
Let us consider ABC is a triangle whose vertices are A(0, 0), B(5, 5), and C(-5, 5)
Now 
AB2 = (√50)2 = 50
Similarly, BC2 = (-5 – 5)2(5 – 5)2
= (-10)2 + (0)2 = 100 + 0 = 100
and CA2 = (0 + 5)2 + (0 – 5)2
= (5)2 + (-5)2 = 25 + 25 = 50
Here, we conclude that AB = CA
Also, AB2 + CA2 = 50 + 50 = 100 = BC2
Hence, the triangle ABC is a right triangle.
Question 33. If the points P (x, y) is equidistant from the points A (5, 1) and B (1,5), prove that x = y.
Solution:
Let us consider P(x, y) is equidistant from the points A (5, 1) and B (1,5),
It is given that PA = PB
Also, PA2 = PB2
Now, PA=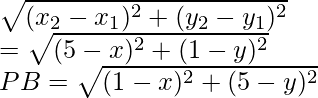
On squaring both sides, we get
(5 – x)2 + (1 – y)2 = (1 – x)2 + (5 – y)2
25 + x2 – 10x + 1 + y2 – 2y = 1 + x2 – 2x + 25 + y2 – 10y
-10x – 2y + 26 = -2x – 10y + 26
-10x – 2y = -2x – 10y
-10x + 2x = -10y + 2y
-8x = -8xy
x = y
Question 34. If Q (0, 1) is equidistant from P (5, -3) and R (x, 6) find the values of x. Also find the distances QR and PR.
Solution:
Given that Q (0, 1) is equidistant from P (5, -3) and R (x, 6)
So, PQ = RQ
Also, PA2 = PB2
Now 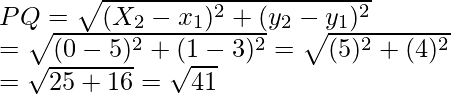
PQ2 = 41
Similarly, RQ2 = (-x)2 + (1 – 6)2
= (-x)2 + (-5)2 = x2 + 25
It is given that PQ = RQ
So,
x2 + 25 = 41
x2 = 41 – 25
x2 = (±4)2
x = ±4
Now, QR = √x2 + 25 = √41
So, when x = 4, then
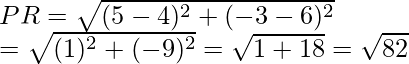
or when x = -4, then
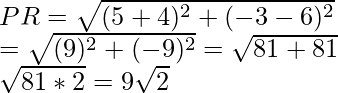
Question 35. Find the values of y for which the distance between the points P (2, -3) and Q (10, y) is 10 units.
Solution:
Given that the distance between P (2, -3) and Q (10, y) = 10
So, 
On squaring both side we get
64 + (y + 3)2 = 100
(y + 3)2 = 100 – 64
(y + 3)2 = 36
y + 3 = (±6)2
So, when y + 3 = 6, then y = 6 – 3 = 3
Or when y + 3 = -6, then y = -6 – 3 = -9
Hence, y = 3, -9
Question 36. If the point P (k – 1, 2) is equidistant from the points A (3, k) and B (k, 5), find the values of k.
Solution:
Given that the point P (k – 1, 2) is equidistant from A (3, k) and B (k, 5)
So, PA = PB
Also, PA2 = PB2
(k – 1 – 3)2 + (2 – k)2 = (k – 1 – k)2 + (2 – 5)2
(k – 4)2 + (2 – k)2 = (-1)2 + (-3)2
k2 – 8k + 16 + 4 – 4k + k2 = 1 + 9
2k2 – 12k + 20 – 10 = 0
2k2 – 12k + 10 = 0
k2 – k – 5k + 5 = 0
k(k – 1) – 5(k – 5) = 0
(k – 1)(k – 5) = 0
Either k – 1 = 0, then k = 1
or k – 5 = 0, then k = 5
Hence, k = 1, 5
Question 37. If the point A (0, 2) is equidistant from the point B (3, p) and C (p, 5), find p. Also, find the length of AB.
Solution:
Given that point A (0, 2) is equidistant from B (3, p) and C (p, 5)
So, AB = AC
Also, AB2 = AC2
(0 – 3)2 + (2 – p)2 = (0 – p)2 + (2 – 5)2
9 + (2 – p)2 = p2 + 9
9 + 4 + p2 – 4p = p2 + 9
p2 – 4p + 13 – p2 – 9 = 0
-4p – 4 = 0
-4p = -4
p = -4/-4 = 1
p = 1
and AB = 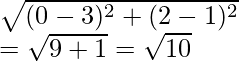
Question 38. Name the quadrilateral formed, if any, by the following points, and give reasons for your answers :
(i) A (-1, -2), B (1, 0), C (-1, 2), D (-3, 0)
(ii) A (-3, 5), B (3, 1), C (0, 3), D (-1, -4)
(iii) A (4, 5), B (7, 6), C (4, 3), D (1, 2)
Solution:

(i) Given points are A (-1, -2), B (1, 0), C (-1, 2), D (-3, 0)
Now 
AB2 = (x2 – x1)2 + (y2 – y1)2
= (1 + 1)2 + (0 + 2)2
= (2)2 + (2)2
= 4 + 4 = 8
Similarly, BC2 = (-1 – 1)2 + (2 – 0)2
= (-2)2 + (2)2
= 4 + 4 = 8
CD2 = (-3 + 1)2 + (0 – 2)2
= (-2)2 + (-2)2
= 4 + 4 = 8
DA2 = (-1 + 3)2 + (-2 + 0)2
= (2)2 + (-2)2
= 4 + 4 = 8
Diagonal AC2 = (-1 + 1)2 + (2 + 2)2
= (0)2 + (4)2 = 0 + 16 = 16
and BD2 = (-3 – 1)2 + (0 – 0)2 = (-4)2 + (0) = 16
Therefore, the sides are equal and diagonals are also equal
Hence, the quadrilateral ABCD is a square.
(ii) Given points are A (-3, 5), B (3, 1), C (0, 3), D (-1, -4)
Now AB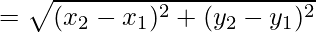
AB2 = (x2 – x1)2 + (y2 – y1)2
= (3 + 3)2 + (1 – 5)2
= (6)2 + (-4)2
= 36 + 16 = 52
Similarly, BC2 = (0 – 3)2 + (3 – 1)2
= (-3)2 + (2)2
= 9 + 4 = 13
CD2 = (-1 – 0)2 + (-4 – 3)2
= (-1)2 + (-7)2
= 1 + 49 = 50
DA2 = (-3 + 1)2 + (5 + 4)2
= (-2)2 + (9)2
= 4 + 81 = 85
Diagonal AC2 = (0 + 3)2 + (3 – 5)2 = (3)2 + (-2)2 = 9 + 4 = 13
In triangle ABC
The length of AB = √52, AC = √13, BC = √13
AC + BC = √13 + √13 = 2√13
= √4 * 13 = √52
AC + BC = AB
Triangle ABC is not possible
Hence, ABCD is not a quadrilateral
(iii) Points A (4, 5), B (7, 6), C (4, 3), D (1, 2)
Now AB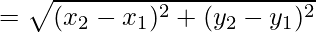
AB2 = (x2 – x1)2 + (y2 – y1)2
= (7 – 4)2 + (6 – 5)2
= (3)2 + (1)2
= 9 + 1 = 10
Similarly, BC2 = (4 – 7)2 + (3 – 6)2
= (3)2 + (-3)2 = 9 + 9 = 18
CD2 = (1 – 4)2 + (2 – 3)2
= (-3)2 + (-1)2
= 9 + 1 = 10
DA2 = (4 – 1)2 + (5 – 2)2 = (3)2 + (3)2 = 9 + 9 = 18
Here AB = CD and BC = DA
Diagonal AC2 = (4 – 4)2 + (3 – 5)2
= (0)2 + (-2)2
= 0 + 4 = 4
and BD2 = (1 – 7)2 + (2 – 6)2 = (-6)2 + (-4)2
= 36 + 16 = 52
Hence the opposite sides are equal and diagonals are not equal.
So, ABCD is a parallelogram.
Question 39. Find the equation of the perpendicular bisector of the line segment joining points (7, 1) and (3, 5).
Solution:
Let the given points are A (7, 1) and B (3, 5) and mid point be M
Coordinates of mid-point AB = ((7 + 3)/2, (1 + 5)/2) = (5, 3)
Now slope of AB(m1)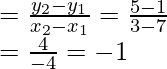
Slope of perpendicular to AB(m2) = -1/m1 = -(-1) = -1
So, the equation of the perpendicular line passing through multiple y – y1 = m(x – x1)
y – 3 = 1(x – 5)
y – 3 = x – 5
x – y = -3 + 5
x – y = 2
Share your thoughts in the comments
Please Login to comment...