Basic Proportionality Theorem

Thales theorem is one of the most fundamental theorems in geometry that relates the parts of the length of sides of triangles. As this theorem is given by the Greek mathematician Thales of Miletus, thus this theorem is called Thales Theorem. The other name of the Thales theorem is Basic Proportionality Theorem or BPT. With the understanding of the Thales Theorem, students can gain foundational knowledge of geometry. In this article, Thales Theorem or Basic Proportionality Theorem is covered with all the necessary details such as statement, proof, and its converse as well. Also, this article covers the sample problems and FAQs based on Thales Theorem.

What is a Similar Triangle?

The concept of Thales’ theorem is based on the understanding of similar triangles. Two triangles are said to be similar if they have the same shape which can be determined using either the angles or the proportions of the sides of any two triangles. In similar triangles, they have two following properties:

• All the corresponding angles of similar triangles are equal, and
• All the sides of both triangles are proportional to each other.

Statement of Thales Theorem

Thales’s Theorem or Basic Proportionality Theorem (BPT) states that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.

Proof of Thales Theorem

Proof of Basic Proportionality Theorem or Thales Theorem is given as follows:

Given: Suppose we have a triangle ABC, if we draw a line LM parallel to side BC.

To Proof: 

Construction: To prove the required result, construct the following lines in the given figure:

• Construct LY⊥AM.
• Construct MX⊥AL.
• Join points L with C and M with B with a line segment.

Proof:

Since, area of triangle= 

Area of  ALM=

Area of  LBM=

Area of  ALM=

Area of  LMC=

Ratio of area of  ALM and  LBM:

. . .(1)

Ratio of area of  ALM and  LMC:

. . .(2)

According to the property of triangles, the triangles on the same base and between same parallel lines have equal areas.

Therefore,  LBM and  LMC have equal areas. 

i.e., area of   LBM = area of  LMC. . .(3)

From equations (1),(2), and (3) we can conclude:

[Hence Proved]

Corollary of Thales Theorem

One of the most important corollaries of the Thales theorem is the Mid Point theorem which states that “if the line is drawn from one of the midpoints of the side of a triangle parallel to the second, then it always intersects the third side at the midpoint as well.”

Converse of Basic Proportionality Theorem

The Converse of the Basic Proportionality Theorem (BPT) or Thales’s Theorem states that if a line intersects two sides of a triangle and divides the sides proportionally, then the line is parallel to the third side of the triangle.

Proof of Converse of Basic Proportionality Theorem

Proof of the converse of the Basic Proportionality Theorem or converse of Thales Theorem is given as follows:

Given: Let us consider a triangle ABC with D and E two points on the side AB and AC such that AD/BD = AE/CE . . .(i).

To Proof: DE∥BC

Construction: To prove the converse of BPT, draw a line DE’∥BC.

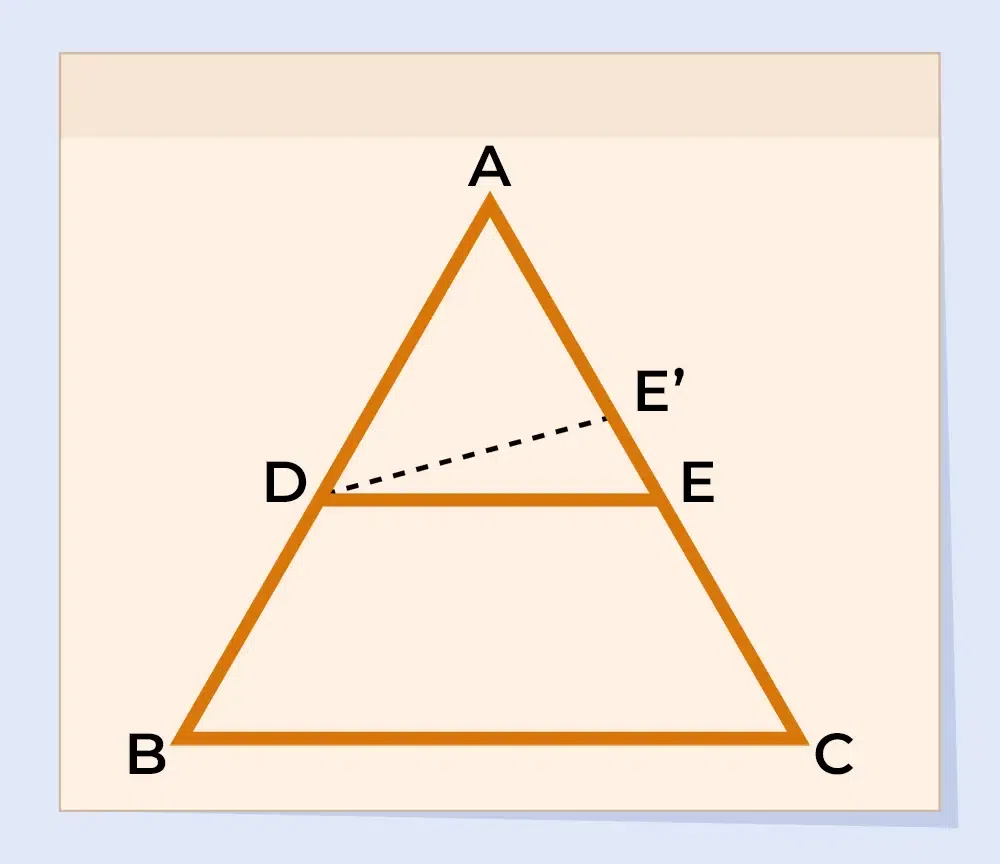
Proof:

Now, as DE’∥BC in triangle ABC, 

Thus, by using the Basic proportionality theorem,

AD/BD = AE’/CE’ . . .(ii)

Using equations (i) and (ii), we get

AE/CE = AE’/CE’

Add 1 to both sides of the equation,

AE/CE + 1 = AE’/CE’ + 1

⇒ (AE+CE)/CE = (AE’+CE’)/CE’

⇒ AC/CE = AC/CE’

⇒ CE = CE’

This can only be possible if E and E’ are coincident.

Thus, E and E’ are the same points. 

As, DE∥BC 

So, DE∥BC [Hence Proved]

Solved Examples on Basic Proportionality Theorem

Example 1: In ΔPQR, X and Y are points on the sides PQ and PR respectively such that XY|| QR. If PX/XQ = 2/5 and PR = 10 cm find PY. 

Solution:

In the given triangle PQR, X and Y are points on the sides PQ and PR respectively such that XY || QR.

By the Basic Proportionality Theorem, we have:

PX/XQ = PY/YR

⇒ PX/XQ = PY/(PR-PY)

Given that PX/XQ = 2/5, we can substitute for PX/XQ:

2/5 = PY/(PR-PY)

⇒ 2/5 = PY/(10-PY)

⇒ 2/5 = PY/(10-PY)

⇒ 2(10 – PY) = 5PY

⇒ 20 – 2PY = 5PY

⇒ 7PY = 20 

⇒ PY = 20 /7

Hence, the length of PY is 20/7 cm.

Example 2: In ΔPQR, X and Y are points on the sides PQ and PR respectively such that XY|| QR. If PX = x − 7 , XQ = x + 3 , PY = 2x and YR = 2x −1 , find the value of x.

Solution:

In the given triangle PQR, X and Y are points on the sides PQ and PR respectively such that XY || QR.

By the Basic Proportionality Theorem, we have:

PX/XQ = PY/YR

⇒ (x – 7)/(x + 3) = 2x/(2x – 1)

⇒ (x – 7)(2x – 1) = 2x(x + 3)

⇒ 2x² – x – 14x +7 = 2x² + 6

⇒ -15x = 6 – 7

⇒ 15x = 1

⇒ x = 1/15

Example 3: In an ∆ABC, sides AB and AC  are intersected by a line at D and E respectively, which is parallel to side BC. Prove that AD/AB = AE/AC.

Solution:

Given: DE || BC. So, AD/DB = AE/EC

or By interchanging the ratios as => DB/AD = EC/AE

Now, add 1 on both sides 

(DB/AD)  + 1 = (EC/AE) + 1

⇒ (DB + AD)/AD = (EC + AE)/AE

⇒ AB/AD = AC/ AE

If we interchange the ratios again, we get

AD/AB = AE/AC [Hence Proved]

Example 4. In triangle ABC, where DE is a line drawn from the midpoint of AB and ends midpoint of AC at E. AD/DB = AE/EC and ∠ADE = ∠ACB. Then prove ABC is an isosceles triangle.

Solution:

Given: AD/DB = AE/EC

By the converse of the basic proportionality theorem, we get => DE || BC

According to question; ∠ADE = ∠ACB

Hence,∠ABC = ∠ACB

The side opposite to equal angles is also equal to AB = AC

Hence, ABC is an isosceles triangle.

FAQs on Basic Proportionality Theorem

Q1: What is the Basic Proportionality Theorem?

Answer:

In simple words, Basic Proportionality Theorem states that the line joining the points on the sides of triangle if parallel then always divide the sides in equal proportions.

Q2: Why Basic Proportionality Theorem is called Thales Theorem?

Answer:

The basic proportionality theorem (BPT) is called Thales Theorem as it is given by the Greek Mathematician cum philosopher Thales of Miletus.

Q3: Can the Basic Proportionality Theorem be applied to any triangle?

Answer:

Yes, Basic Proportionality Theorem can be applied to any triangle regardless of its size and shape.

Q4: Can the Thales Theorem be applied if the line joining the sides is not parallel to the base of the triangle?

Answer:

No, the Thales Theorem can only be applied if the line joining the sides of a triangle is parallel as it is the necessary condition for the theorem.

Q5: What is the converse of the Basic Proportionality Theorem?

Answer:

Converse of the Basic Proportionality Theorem states that if a line intersects two sides of a triangle and divides the sides proportionally, then the line is parallel to the third side of the triangle.