Quadratic equations are the equations where a polynomial has degree two. Roots of Quadratic Equations are the values of the variable that satisfies the equation.
Let’s learn how to find the roots of quadratic equation formulas with the help of solved examples.
Roots of Quadratic Equation
Roots of a Quadratic Equation are the values of the variable let’s say x for which the equation gets satisfied.
- Roots of Quadratic Equations are also called Zeros of a Quadratic Equation or Solutions of a Quadratic Equation.
- Quadratic equations are mathematical expressions of the form ax2 + bx + c = 0, where a, b, and c are constants, and x represents the variable.
- Solving for the values of x that make this equation true yields the roots of the quadratic equation.
Methods to Find Roots
The methods to find Roots or Zeroes of a Quadratic Equation are :
- Factoring
- Quadratic Formula
- Completing the Square
- Graphical Method
How to Find Roots of Quadratic Equation?
To Find roots of Quadratic Equations follow the methods mentioned below:
Finding Roots of Quadratic Equation by Quadratic Formula
x = [-b±√(b2 – 4ac)]/2a
Example: The length of sides of a rectangle is given by x – 3 and x – 5 and the area of the rectangle is 3 unit2. Find the sides of the rectangle.
Solution:
Area of rectangle = length*breadth = (x – 3)(x – 5) = 3
Area = x2 – 8x + 15 = 3
= x2 – 8x + 12 = 0
Discriminant = b2 – 4ac = 64 – (4(1)(12)) = 64 – 48 = 16
x = [-b ± √(b2-4ac)]/2a = [-(-8) ± √16]/2 = (8±4)/2
x = 12/2 or 4/2
x = 2 or 6
When x is 2, sides are x – 3 = 2 – 3 = -1 and x – 5 = 2 – 5 = -3.
Since length of sides cannot be equal therefore x = 2 is not a valid ans.
When x is 6, sides are x – 3 = 6 – 3 = 3 and x – 5= 6 – 5 =1.
Therefore, x = 6 is the valid answer and the sides are 3 and 1.
Finding Roots of Quadratic Equation by Factoring
A quadratic equation can be considered a factor of two terms. Like ax2 + bx + c = 0 can be written as (x – x1)(x – x2) = 0 where x1 and x2 are roots of quadratic equation.
Steps:
- Find two numbers such that there product = ac and their sum = b.
- Then write x coefficient as sum of these two numbers and split them such that you get two terms for x.
- factor the first two as a group and last two terms as a group.
- Take common factors from these and on equating the two expression with zero after taking common factors and rearranging the equation we get the roots .
Example: Let be the quadratic equation x2 + 3x = 18
x2 + 3x – 18 = 0
Step:
1. 6 and -3 are the numbers whose sum is equal to b and product is equal ac.
2. x2 + (6-3)x – 18 = x2 + 6x -3x – 18 =0
3. x(x + 6) – x(x + 6) = 0
4. taking (x + 6) as common.
(x + 6)(x – 3) = 0
x = -6 or x = 3
In a factorizing method it is not necessary that you will always find these two numbers easily(especially in the case when roots are imaginary or irrational) so it is better to use the quadratic formula.
Nature of Roots
The nature of roots depends on the discriminant of the quadratic equation. The discriminant of a quadratic equation is given by b2 – 4ac. It is so because in quadratic formula square root of discriminant is there.
Root 1: If b2 – 4ac > 0 roots are real and different. As the discriminant is >0 then the square root of it will not be imaginary. It has two cases.
- If b2 – 4ac is a perfect square then roots are rational. As the discriminant is a perfect square, so we will have an integer as a square root of the discriminant. Hence, the roots are rational numbers.
Example: Let the quadratic equation be x2-5x+6=0.
Then the discriminant of the given equation is b2 – 4ac=(-5)2 – 4×1×6 = 25-24 = 1
According to Shridharacharaya formula
x = [-b±√(b2-4ac)]/2a = x = [-(-5) ± √1]/2
x1 = [-(-5) + √1]/2 = 6/2 = 3
x2 = [-(-5) – √1]/2 = 4/2 = 2
Therefore, the roots are 3,2. Both are rational and different.
- If b2 – 4ac is not a perfect square then the square root of discriminant is irrational hence roots are irrational and occurs in pair.
Example: Let the quadratic equation be x2-7x+8 = 0.
Then the discriminant of the given equation is
b2 – 4ac=(-7)2 – 4*1*8 = 49-32 = 17
According to Shridharacharaya formula
x = [-b±√(b2-4ac)]/2a = x = [-(-7) ± √17]/2
x1 = [-(-7) + √17]/2 = [7 + √17]/2
x2 = [-(-7) – √17]/2 = [7 – √17]/2
Therefore, the roots are [7 + √17]/2,[7 – √17]/2. Both are irrational and in pairs.
Root 2: If b2 – 4ac = 0 roots are real and equal.
Example: Let the quadratic equation be 3x2-6x+3=0.
Then the discriminant of the given equation is
b2 – 4ac=(-6)2 – 4*3*3 = 36 – 36 = 0
According to Shridharacharaya formula
x = [-b±√(b2-4ac)]/2a = x = [-(-6) ± √0]/[(2)(3)]
x1 = [-(-6) + √0]/2 = 6/6 = 1
x2 = [-(-6) – √0]/2 = 6/6 = 1
Therefore, the roots are 1,1. Both are real and equal.
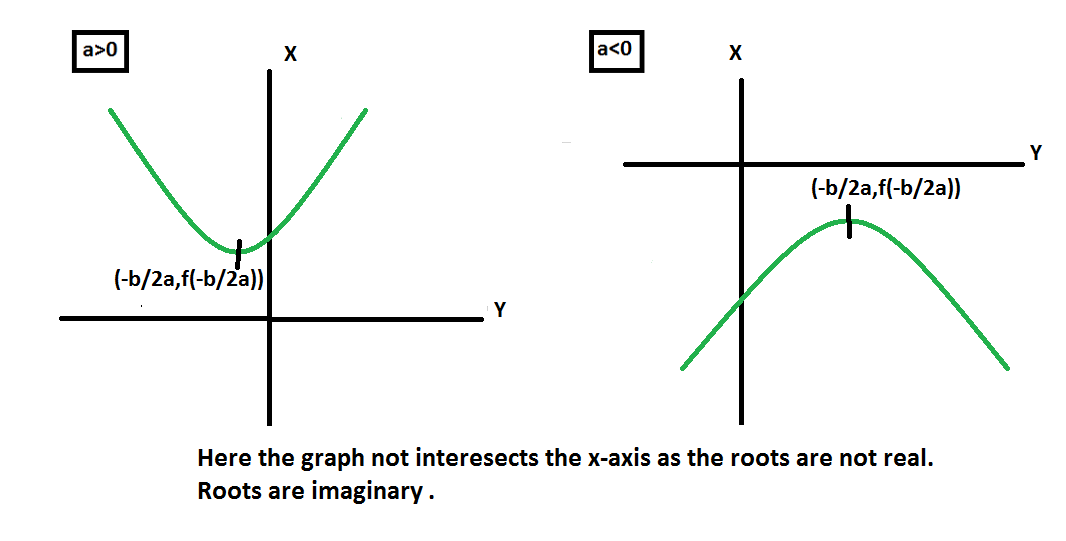
Root 3: If b2 – 4ac < 0 roots are imaginary, or you can say complex roots. It is imaginary because the term under the square root is negative. These complex roots will always occur in pairs i.e, both the roots are conjugate of each other.
Example: Let the quadratic equation be x2+6x+11=0.
Then the discriminant of the given equation is
b2 – 4ac=(6)2 – 4*1*11 = 36-44 = -8
According to Shridharacharaya formula
x = [-b±√(b2-4ac)]/2a = x = [-(6) ± √(-8)]/2
x1 = [-(6) + √(-8)]/2 = [-6 + √8i]/2 = 2[-3 + √2i]/2 = -3 + √2i
x2 = [-(6) – √(-8)]/2 = [-6 – √8i]/2 = 2[-3 – √2i]/2 = -3 – √2i
Therefore, the roots are 3,2. Both are imaginary and conjugate of each other(in pair).
Learn More :
Graphs for Roots
The maximum/minimum value of quadratic function is found at x = -b/2a
Proof:
We get maxima or minima when d(f(x))/dx = 0.
On differentiating quadratic function f(x) = ax2 + bx + c.
We get,
2ax + b = 0
x = -b/2a
This x is either maxima(a<0) or minima(a>0).
1. When D > 0
Graph of b2– 4ac > 0 is shown below:

2. When D = 0
Graph of b2– 4ac = 0 is shon below:

3. When D < 0
Graph of b2– 4ac < 0 is shown below:
Related :
Examples on Roots of Quadratic Equation
Question 1. The height of a triangle is less than 4 cm than the base. The area of triangle is 30 cm2. Find the height and base of triangle.
Solution:
Let the base of triangle be x cm then height is x-4 cm
Area of triangle = 1/2*height*base = 1/2*(x)(x – 4)=30
Area = x2 – 4x = 30*2
= x2 – 4x = 60
= x2 – 4x – 60 = 0
Discriminant = (-4)2 – 4(1)(-60) = 16+240 = 256
x = [-b±√(b2 – 4ac)]/2a = [-(-4)±√256]/2 = (4±16)/2
x = 20/2 or -12/2
x = 10 or -6
As side cannot be negative, therefore -6 is not correct.
So, when x is 10, base =10 cm and height =x – 4 = 10 – 4 = 6 cm
Therefore, x = 10 is the valid answer and the base and height of the triangle are 10 and 6 respectively.
Question 2. The volume of a box is 600 inch2 . The length of box is 2 inches less than the width. The height of box is 5 inches . Find the dimensions of box.
Solution:
Let the width of box be x inches then length = x – 2 inches.
Volume of box =Length* Width *Height = (x-2)(x)5= 600
x2 – 2x = 120 => x2 – 2x -120 = 0
x2 + 10x – 12x – 120 = 0
x(x + 10) – 12(x + 10)=0
(x – 12)(x + 10)=0
x = 12 or x = -10
As width can not be negative, therefore, -10 is not correct.
When x = 12, width = 12 inches, length = x – 2 = 12 – 2 = 10 inches, height = 5 inches
Question 3. A ball is thrown from the top of a building . its height in meters above the ground as a function of time is given by h(t) = -4t2 + 24t + 3. a) How much time it take to reach the maximum height and what is the maximum height. b) Find also the time at which ball hits the ground.
Solution:
a) Since a<0, therefore the time to reach maximum height is = -b/2a. (refer graph part)
t = -24/(2(-4)) = -24/-8
t = 3 sec.
Height = h(t) = -4(3)2 +24(3)+3 = 39 meters.
b) When the ball hits the ground h(t)=0.
-4t2 + 24t + 3 = 0
The discriminant of the given equation is
b2 – 4ac=(24)2 – 4×(-4)×3 = 576 + 48 = 624
According to Quadratic formula
x = [-b±√(b2-4ac)]/2a = x = [-(24) ± √624]/[(2)(-4)]
x1 = [-24 + √624]/-8= 4 [-6 + √39]/-8 = [-6 + √39]/-2 = [6 – √39]/2 = -0.122499 = -0.1225(approx)
x2 = [-24 – √624]/-8= 4 [-6 – √39]/-8 = [-6 – √39]/-2 = [6 + √39]/2 = 6.122499 = 6.1225(approx)
As time can not be negative, therefore, [6 – √39]/2 sec is not correct.
Therefore, the ball hits the ground at [6 + √39]/2 = 6.122499 = 6.1225 sec
Practice Problems on Roots of Quadratic Equations
Problem 1: Find the roots of the following Quadratic Equations:
- 3x2 – 7x + 2 = 0
- x2 + 4x + 4 = 0
- 2x2 + 5x – 3 = 0
- 4x2 – 12x + 9 = 0
- x2 – 6x + 9 = 0
Problem 2: The sum of two consecutive integers is 31. Find the two integers.
Problem 3: A quadratic equation of the form ax2 + bx + c = 0 has roots x = 3 and x = -2. Find the values of a, b and c.
Problem 4: A ball is thrown into the air from a height of 5 feet with an initial velocity of 40 feet per second. The height h of the ball above the ground after t seconds can be modelled by the quadratic equation h(t) = -16t2 + 40t + 5. How long does it take for the ball to reach its maximum height?
FAQs on Roots of Quadratic Equations
What is Quadratic Equation?
A quadratic equation is a polynomial equation of the second degree, typically written in the form ax2 + bx + c = 0, where a, b, and c are constants, and x is the variable.
What are the Roots of a Quadratic Equation?
The roots of a quadratic equation are the values of ‘x’ that satisfy the equation, making it equal to zero. These are the values where the graph of the quadratic function intersects the x-axis.
How do you Find the Roots of Quadratic Equation?
You can find the roots of a quadratic equation using the quadratic formula, i.e., x = (-b ± √(b2 – 4ac)) / (2a).
Other than this, we can also find roots using the methods such as factoring and completing the square.
How many Roots Can a Quadratic Equation Have?
A quadratic equation can have either two real roots, one real root (a repeated root), or two complex roots (conjugate pair of complex numbers).
Can a Quadratic Equation have no Real Roots?
Yes, if the discriminant is negative (b2 – 4ac < 0), the quadratic equation will have two complex roots and no real roots.
How do you Determine the Nature of the Roots of Quadratic Equation?
You can determine the nature of the roots by calculating the discriminant (b2 – 4ac) and examining its value in relation to zero.
- If discriminant > 0, two real roots,
- If discriminant = 0, one real repeated root, and
- If discriminant < 0, two complex roots i.e., no real roots.
What is the Sum and Product of the Roots of Quadratic Equation?
For a quadratic equation in the form ax2 + bx + c = 0, the sum of the roots is -b/a, and the product of the roots is c/a.
What are Four Types of Roots of Quadratic Equations?
Four types of roots in quadratic equations are:
- Two Real and Distinct Roots
- Two Real and Equal Roots
- One Real and Repeated Root
- Two Complex Roots
Why are Alpha (α) and Beta (β) used to Represent Roots of Quadratic Equation?
Alpha (α) and beta (β) are commonly used to represent the roots of a quadratic equation for simplicity and consistency in mathematical notation.
Share your thoughts in the comments
Please Login to comment...