Class 10 RD Sharma Solutions – Chapter 6 Trigonometric Identities – Exercise 6.1 | Set 2
Last Updated :
30 Apr, 2021
Prove the following trigonometric identities:
Question 29. 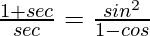
Solution:
We have,
L.H.S. = 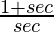
= 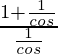
= 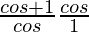
= 1 + cos θ
= 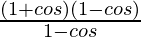
= 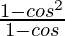
= 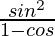
= R.H.S.
Hence proved.
Question 30. 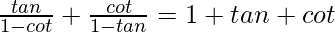
Solution:
We have,
L.H.S. = 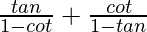
= 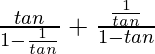
= ![Rendered by QuickLaTeX.com \frac{1}{1-tanθ}[\frac{1}{tanθ}-tan^2θ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0df38adc2314f3e63eed2fe87487d31d_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{1-tanθ}[\frac{1-tan^3θ}{tanθ}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a1b491a4c45fc79cc901b052ef64f14_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{1-tanθ}\left[\frac{(1-tanθ)(1+tanθ+tan^2θ)}{tanθ}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0de043372ca96eee1b760730f703ce8_l3.png)
= 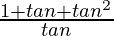
= 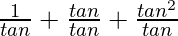
= 1 + tanθ + cotθ
= R.H.S.
Hence proved.
Question 31. sec6 θ = tan6 θ + 3 tan2 θ sec2 θ + 1
Solution:
We know,
sec2 θ − tan2 θ = 1
On cubing both sides, we get,
=> (sec2θ − tan2θ)3 = 1
=> sec6 θ − tan6 θ − 3sec2 θ tan2 θ(sec2 θ − tan2 θ) = 1
=> sec6 θ − tan6 θ − 3sec2 θ tan2 θ = 1
=> sec6 θ = tan6 θ + 3sec2 θ tan2 θ + 1
Hence proved.
Question 32. cosec6 θ = cot6 θ + 3cot2 θ cosec2 θ + 1
Solution:
We know,
cosec2 θ − cot2 θ = 1
On cubing both sides,
=> (cosec2 θ − cot2 θ)3 = 1
=> cosec6 θ − cot6 θ − 3cosec2 θ cot2 θ (cosec2 θ − cot2 θ) = 1
=> cosec6 θ − cot6 θ − 3cosec2 θ cot2 θ = 1
=> cosec6 θ = cot6 θ + 3 cosec2 θ cot2 θ + 1
Hence proved.
Question 33. 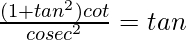
Solution:
We have,
L.H.S. = 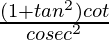
= 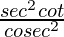
= 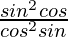
= sin θ/cos θ
= tan θ
= R.H.S.
Hence proved.
Question 34. 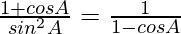
Solution:
We have,
L.H.S. = 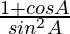
= 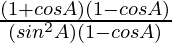
= 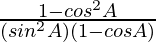
= 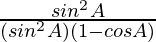
= 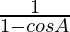
= R.H.S.
Hence proved.
Question 35. 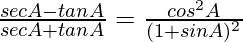
Solution:
We have,
L.H.S. = 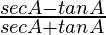
= 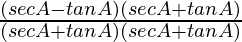
= 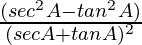
= 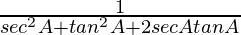
= 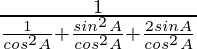
= 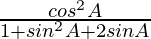
= 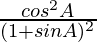
= R.H.S.
Hence proved.
Question 36. 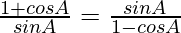
Solution:
We have,
L.H.S. = 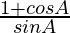
= 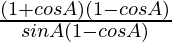
= 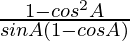
= 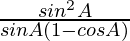
= 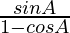
= R.H.S.
Hence proved.
Question 37. (i) 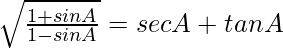
Solution:
We have,
L.H.S. = 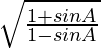
= 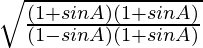
= 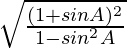
= 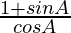
= 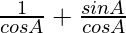
= sec A + tan A
= R.H.S.
Hence proved.
(ii) 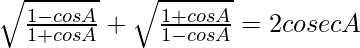
Solution:
We have,
L.H.S. = 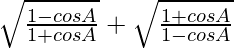
= 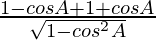
= 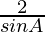
= 2 cosec A
= R.H.S.
Hence proved.
Question 38. (i) 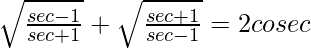
Solution:
We have,
L.H.S. = 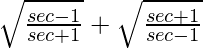
= 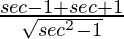
= 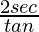
= 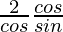
= 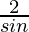
= 2 cosec θ
= R.H.S.
Hence proved.
(ii) 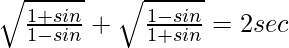
Solution:
We have,
L.H.S. = 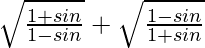
= 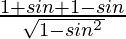
= 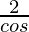
= 2 sec θ
= R.H.S.
Hence proved.
(iii) 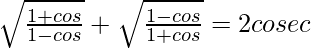
Solution:
We have,
L.H.S. = 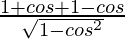
= 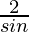
= 2 cosec θ
= R.H.S.
Hence proved.
(iv) 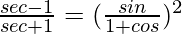
Solution:
We have,
L.H.S. = 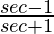
= 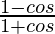
= 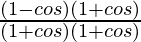
= 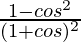
= 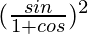
= R.H.S.
Hence proved.
Question 39. (sec A – tan A)2 = 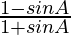
Solution:
We have,
L.H.S. = (sec A – tan A)2
= 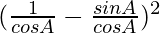
= 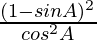
= 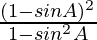
= 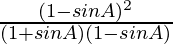
= 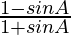
= R.H.S.
Hence proved.
Question 40. 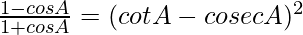
Solution:
We have,
L.H.S. = 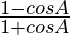
= 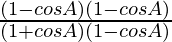
= 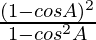
= 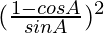
= (cosec A – cot A)2
= (cot A – cosec A)2
= R.H.S.
Hence proved.
Question 41. 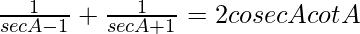
Solution:
We have,
L.H.S. = 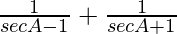
= 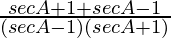
= 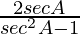
= 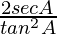
= 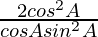
= 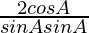
= 2 cosec A cot A
= R.H.S.
Hence proved.
Question 42. 
Solution:
We have,
L.H.S. = 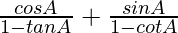
= 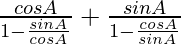
= 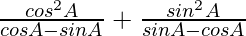
= 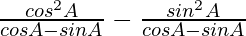
= 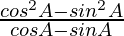
= 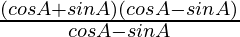
= sin A + cos A
= R.H.S.
Hence proved.
Question 43. 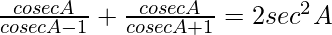
Solution:
We have,
L.H.S. = 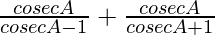
= 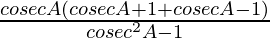
= 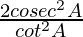
= 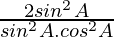
= 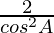
= 2 sec2 A
= R.H.S.
Hence proved.
Question 44. 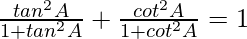
Solution:
We have,
L.H.S. = 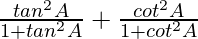
= 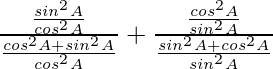
= 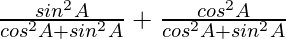
= 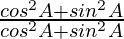
= 1
= R.H.S.
Hence proved.
Question 45. 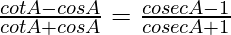
Solution:
We have,
L.H.S. = 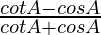
= 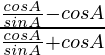
= 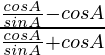
= 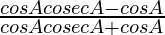
= 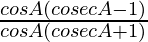
= 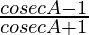
= R.H.S.
Hence proved.
Question 46. 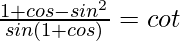
Solution:
We have,
L.H.S. = 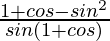
= 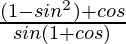
= 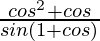
= 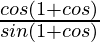
= 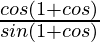
= cos θ/sin θ
= cot θ
= R.H.S.
Hence proved.
Question 47. (i) 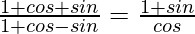
Solution:
We have,
L.H.S. = 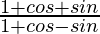
= 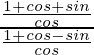
= 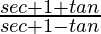
= 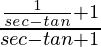
= 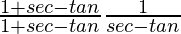
= 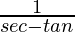
= 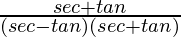
= sec θ + tan θ
= 1/cos θ + sin θ/cos θ
= 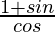
= R.H.S.
Hence proved.
(ii) 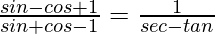
Solution:
We have,
L.H.S. = 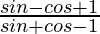
= 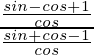
= 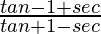
= 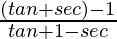
= 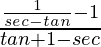
= 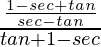
= 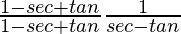
= 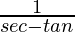
= R.H.S.
Hence proved.
Question 48. 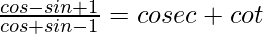
Solution:
We have,
L.H.S. = 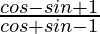
= 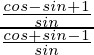
= 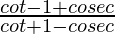
= 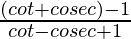
= 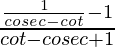
= 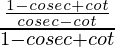
= 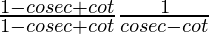
= 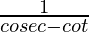
= 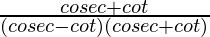
= cosec θ + cot θ
= R.H.S.
Hence proved.
Question 49. (sin θ + cos θ) (tan θ + cot θ) = sec θ + cosec θ
Solution:
We have,
L.H.S. = (sin θ + cos θ) (tan θ + cot θ)
= sin2 θ/cosθ + cos θ + sin θ + cos2 θ/sin θ
= sin θ (1 + tan θ) + (cos θ/tan θ) (1 + tan θ)
= (1 + tan θ) (sin θ + cos θ/tan θ)
= 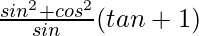
= 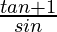
= sec θ + cosec θ
= R.H.S.
Hence proved.
Question 50. 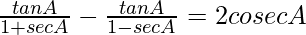
Solution:
We have,
L.H.S. = 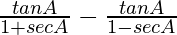
= 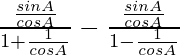
= 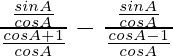
= 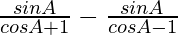
= 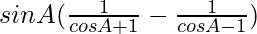
= 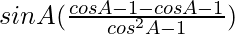
= 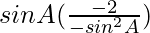
= 2/sin A
= 2 cosec A
= R.H.S.
Hence proved.
Question 51. 1 + 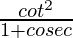 = cosec θ
= cosec θ
Solution:
We have,
L.H.S. = 1 + 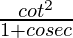
= 1 + 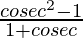
= 1+ 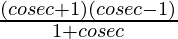
= 1 + cosec θ − 1
= cosec θ
= R.H.S.
Hence proved.
Question 52. 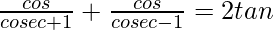
Solution:
We have,
L.H.S. = 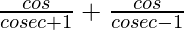
= 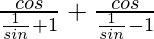
= 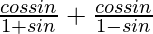
= 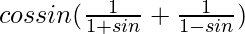
= 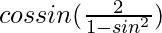
= 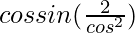
= 2 sin θ/cos θ
= 2 tan θ
= R.H.S.
Hence proved.
Question 53. (1 + tan2 A) + (1 + 1/tan2 A) = 1/(sin2 A − sin4 A)
Solution:
We have,
L.H.S. = (1 + tan2 A) + (1 + 1/tan2 A)
= (1 + sin2 A/cos2 A) + (1 + cos2 A/sin2 A)
= 1/cos2 A + 1/sin2 A
= 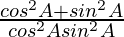
= 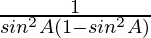
= 1/(sin2 A − sin4 A)
= R.H.S.
Hence proved.
Question 54. sin2 A cos2 B − cos2 A sin2 B = sin2 A − sin2 B
Solution:
We have,
L.H.S. = sin2 A cos2 B − cos2 A sin2 B
= sin2 A (1 − sin2 B) − sin2 B (1 − sin2 A)
= sin2 A− sin2 A sin2 B − sin2 B + sin2 A sin2 B
= sin2A − sin2 B
= R.H.S.
Hence Proved.
Question 55. (i) 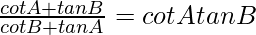
Solution:
We have,
L.H.S. = 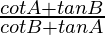
= 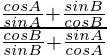
= 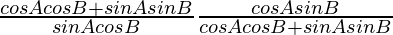
= 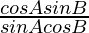
= cot A tan B
= R.H.S.
Hence proved.
(ii) 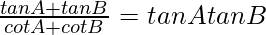
Solution:
We have,
L.H.S. = 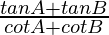
= 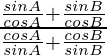
= 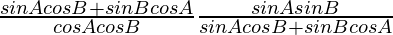
= 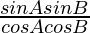
= tan A tan B
= R.H.S.
Hence proved.
Question 56. cot2 A cosec2 B − cot2 B cosec2 A = cot2 A − cot2B
Solution:
We have,
L.H.S. = cot2 A cosec2 B − cot2 B cosec2 A
= cot2 A (1 + cot2 B) − cot2 B (1 + cot2 A)
= cot2 A + cot2 A cot2 B − cot2 B − cot2 B cot2 A
= cot2 A − cot2 B
= R.H.S.
Hence proved.
Share your thoughts in the comments
Please Login to comment...