Question 1. Determine the nature of the roots of following quadratic equations :
(i) 2x² – 3x + 5 = 0
(ii) 2x² – 6x + 3 = 0
(iii) 3/5 x² – 2/3 x + 1 = 0
(iv) 3x² – 4√3 x + 4 = 0
(v) 3x² – 2√6 x + 2 = 0
Solution:
(i) 2x² – 3x + 5 = 0
Here a=2, b=-3, c=5
D=b2-4ac=(-3)2-4*2*5
=-9-40=-31
D<0
Roots are not real
(ii) 2x² – 6x + 3 = 0
Here a=2, b=-6, c=3
D=b2-4ac
=(-6)2-4*2*3=36-24=12
D>0
Roots are real and distinct
(iii) 3/5 x² – 2/3 x + 1 = 0
Here a=3/5, b=-2/3, c=1
Discriminant (D)=b2-4ac
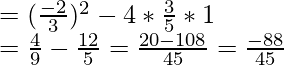
D<0
Roots are not real
(iv) 3x² – 4√3 x + 4 = 0
Here a=3, b=-4√3, c=4
D=b2-4ac
=(-4√3)2-4*3*4=48-48=0
D=0
Roots are real and equal
(v) 3x² – 2√6 x + 2 = 0
Here a=3, b=– 2√6, c=2
Discriminant (D)=b2-4ac
=(– 2√6)2-4*3*2=24-24=0
D=0
Roots are real and equal
Question 2. Find the values of k for which the roots are real and equal in each of the following equations :
(i) kx² + 4x + 1 = 0
Solution:
Here a=k, b=4, c=1
Discriminant(D)=b2-4ac
=(4)2-4*k*1
=16-4k
Roots are real and equal
D=0
16-4k=0⇒4k=16
k=16/4=4
Hence k=4
(ii) kx² – 2√5 x + 4 = 0
Solution:
Here a=k, b=-2√5, c=4
Discriminant(D)=b2-4ac
=( – 2√5 )-4*k*4=20-16k
Roots are real and equal
D=0
20-16k=0⇒ 16k=20
k=20/16=5/4
Hence k=5/4
(iii) 3x² – 5x + 2k = 0
Solution:
Here a=3, b=-5, c=2k
Discriminant (D)=b2-4ac
=(-5)2-4*3*2k
=25-24k
Roots are real and equal
D=0
25-24k=0⇒24k=25
k=25/24
(iv) 4x²+ kx + 9 = 0
Solution:
Here a=4, b=k, c=9
Discriminant (D)=b2-4ac
=k2-4*4*9=k2-144
Roots are real and equal
k2-144=0⇒k2=144=(±12)2
(v) 2kx² – 40x + 25 = 0
Solution:
Here a=2k, b=-40, c=25
Discriminant(D)=b2-4ac
=(-40)2-4*2k*25
=1600-200k
Roots are real and equal
D=0
1600-200k=0⇒200k=1600
k=1600/200=8
Hence k=8
(vi) 9x² – 24x + k = 0
Solution:
Here a=9, b=-24, c=k
Discriminant(D)=b2-4ac
=(-24)2-4*9*k
=576-36k
Roots are real and equal
D=0
576-36k=0
36k=576⇒k=576/36=16
k=16
(vii) 4x² – 3kx +1 = 0
Solution:
Here a=4, b=-3k, c=1
Discriminant (D)=b2-4ac
=(-3k)2-4*4*1
=9k2-16
Roots are real and equal
D=0
9k2-16=0⇒9k2=16
k2=16/9=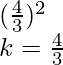
(viii) x² – 2 (5 + 2k) x + 3 (7 + 10k) = 0
Solution:
Here a=1, b=-2(5+2k) and c=3(7+10k)
Discriminant (D)=b2-4ac
[-2(5+2k)]2-4*1*3(7+10k)
=4(25+4k2+20k)-12(7+10k)
=100+16k2+80k-84-120k
16k2-40k+16
Roots are real and equal
D=0
16k2-40k+16=0
2k2-5k+2=0
2k2-4k-k+2=0
2k(k-2)-1(k-2)=0
(k-2)(2k-1)=0
Either k-2=0, then k=2 or 2k-1=0, then 2k=1⇒k=1/2
Hence, k=2, 1/2
(ix) (3k + 1) x² + 2(k + 1) x + k = 0
Solution:
Here a=3k+1, b=2(k+1), c=k
Discriminant(D)=b2-4ac
=[2(k+1)]2-4*(3k+1)*k
=4(k2+2k+1)-4k(3k+1)
=4k2+8k+4-12k2-4k
-8k2+4k+4
Roots are real and equal
D=0
-8k2+4k+4=0
2k2-k-1=0 (Dividing by -4)
2k2-2k+k-1= {Therefore -2=-2*1
-1=-2+1}
2k(k-1)+1(k-1)=0
(k-1)(2k+1)=0
Either k-1=0, then k=1 or 2k+1=0, then 2k=-1⇒k=-1/2
k=1,-1/2
(x) kx² + kx + 1 = – 4x² – x
Solution:
kx² +4x2+kx+x+1=0
(k+4)x2+(k+1)x+1=0
Here a=k+4, b=k+1, c=1
Discriminant(D)=b2-4ac
=(k+1)2-4*(k+4)*1
=k2+2k+1-4k-16
=k2-2k-15
Roots are real and equal
D=0
k2-2k-15=0
k2-5k+3k-15=0 {Therefore -15=-5*3
-2=-5+3}
k(k-5)+3(k-5)=0
(k-5)(k+3)=0
Either k-5=0, then k=5
or k+3=0, then k=-3
Hence k=5,-3
(xi) (k + 1) x² + 2 (k + 3) x + (k + 8) = 0
Solution:
Here a=k+1, b=2(k+3), c=k+8
Discriminant(D)=b2-4ac
=[2(k+3)]2-4(k+1)(k+8)
=4(k2+6k+9)-4)(k2+9k+8)
=4k2+24k+36-4k2-36k-32
=-12k+4
Roots are real and equal
D=0
-12k+4=0
12k=4⇒k=4/12=1/3
Hence k=1/3
(xii) x² – 2kx + 7k – 12 = 0
Solution:
Here a=1, b=-2k, c=(7k-12)
Discriminant(D)=b2-4ac
=(-2k)2-4*1*(7k-12)
=4k2-4(7k-12)
=4k2-28k+48
Roots are real and equal
D=0
4k2-28k+48=0
k2-7k+12=0 (Dividing by 4 )
k2-3k-4k+12=0 {12=-3*(-4)
-7=-3-4}
k(k-3)-4(k-3)=0
(k-3)(k-4)=0
Either, k-3=0, then k=3
or k-4=0, then k=4
Therefore, k=3,4
(xiii) (k + 1) x² – 2 (3k + 1) x + 8k + 1 = 0
Solution:
Here a=k+1, b=-2(3k+1), c=8k+1
Discriminant(D)=b2-4ac
=[-2(3k+1)2-4*(k+1)(8k+1)]
=4(9k2+6k+1)-4(8k2+9k+1)
=36k2+24k+4-32k2-36-4
=4k2-12k
Roots are real and equal
D=0
4k2-12k=0
k2-3k=0 ————–(Dividing by 4)
k(k-3)=0
Either k=0
or k-3=0, then k=3
k=3,0
(xiv) 5x² – 4x + 2 + k (4x² – 2x – 1) = 0
Solution:
5x2-4x+2+4kx2-2kx-k=0
(5+4k)x2-(4+2k)x+(2-k)=0
Here a=5+4k, b=-(4+2k), c=2-k
Discriminant (D)=b2-4ac
=[-(4+2k)]2-4*(5+4k)(2-k)
=16+4k2+16k-4(10-5k+8k-4k2)
=16+4k2+16k-40+20k-32k+16k2
=20k2+4k-24
Roots are real and equal
D=0
20k2+4k-24=0
5k2+k-6=0 —–(Dividing by 4)
5k2+6k-5k-6=0
k(5k+6)-1(5k+6)=0
(5k+6)(k-1)=0
Either 5k+6=0, then 5k=-6⇒k=-6/5
or k-1=0, then k=1
k=1,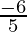
(xv) (4 – k) x² + (2k + 4) x (8k + 1) = 0
Solution:
Here a=4-k, b=2k+4, c=8k+1
Discriminant (D)=b2-4ac
=(2k+4)2-4*(4-k)(8k+1)
=4k2+16k+16-4(32k+4-8k2-k)
=4k2+16k+16-128k-16+32k2+4k
=36k2-108k
Roots are real and equal
36k2-108k=0
k2-3k=0⇒k(k-3)=0
Either k=0
or k-3=0, then k=3
Hence k=0,3
(xvi) (2k + 1) x² + 2 (k + 3) x (k + 5) = 0
Solution:
Here a=2k+1, b=2(k+3), c=k+5
Discriminant (D)=b2-4ac
=[2(k+3)]2-4(2k+1)(k+5)
=4(k2+6k+9)-4(2k2+10k+k+5)
=4k2+24k+36-8k2-40k-4k-20
=-4k2-20k+16
Roots are real and equal D=0
-4k2-20k+16=0
k2+5k-4=0 ———-(Dividing by -4)
Here a=1, b=5, c=-4
Discriminant (D)=b2-4ac
=(5)2-4*1*(-4)=25+16=41
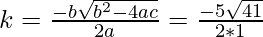
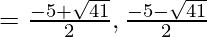
(xvii) 4x² – 2 (k + 1) x + (k + 4) = 0
Solution:
Here a=4, b=-2(k+1), c=k+4
Discriminant (D)=b2-4ac
=[-2(k+1)]2-4*4*(k+4)
=4(k2+2k+1)-16(k+4)
=4k2+8k+4-16k-64
=4k2-8k-12
Roots are real and equal
D=0
4k2-8k-60=0
k2-2k-15=0 ————-(Dividing by 4)
k2-5k+3k-15=0
k(k-5)+3(k-5)=0
(k-5)(k+3)=0
Either k-5=0, then k=5
or k+3=0, then k=-3
k=5,-3
(xviii) 4x² (k + 1) x + (k + 1) = 0
Solution:
Here a=4, b=-2(k+1), c=k+1
Discriminant (D)=b2-4ac
=[-2(k+1)]2-4*4*(k+1)
=4(k2+2k+1)-16(k+1)
=4k2+8k+4-16k-16
=4k2-8k-12
k2-2k-3=0 ————(Dividing by 4)
k2-3k2+k-3=0
k(k-3)+(k-3)=0
(k-3)(k+1)=0
Either (k-3)=0, then k=3
or (k+1)=0, then k=-1
k=-1,3
Question 3. In the following, determine the set of values of k for which the given quadratic equation has real roots:
(i) 2x² + 3x + k = 0
Solution:
Here a=2, b=3, c=k
Discriminant (D)=b2-4ac
=(3)2-4*2*k
=9-8k
The roots are real
D≥0
9-8k≥0⇒9≥8k⇒8k≤9
k≤9/8
(ii) 2x² + x + k = 0
Solution:
Here a=2, b=1, c=k
Discriminant (D)=b2-4ac
=(1)2-4*2*k
=1-8k
The roots are real
D≥0
1-8k≥0⇒1≥8k
8k≤1
k≤1/8
(iii) 2x² – 5x – k = 0
Solution:
Discriminant (D)=b2-4ac
=(-5)2-4*2*(-k)
=25+8k
Roots are real
D≥0
25+8k≥0
8k≥-25⇒≥-25/8
k≥-25/8
(iv) kx² + 6x + 1 = 0
Solution:
Discriminant (D)=b2-4ac
=(6)2-4*k*1
=36-4k
Roots are real
D≥0⇒36-4k≥0
36≥4k⇒4k≤36
k≤36/4⇒k≤9
k≤9
(v) 3x² + 2x + k = 0
Solution:
Here a=3, b=2, c=k
Discriminant (D)=b2-4ac
=(2)2-4*3*k=4-12k
Roots are real
D≥0⇒4-12k≥0
4≥12k⇒12k≤0
4≥12k⇒12k≤4
k≤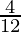 ⇒k≤1/3
⇒k≤1/3
Question 4. Find the values of k for which the following equations have real and equal roots :
(i) x²- 2(k + 1) x + k² = 0
Solution:
Here a=1, b=2(k+1), c=k2
Discriminant (D)=b2-4ac
=[2(k+1)]2-4*1*k2
=4(k2+2k+1)-4k2
=4k2+8k+4-k2
=8k+4
Roots are real and equal
D=0
8k+4=0⇒8k=-4
k=-4/8=-1/2, Hence k=-1/2
(ii) k²x² – 2 (2k – 1) x + 4 = 0
Solution:
Here, a=k2, b=-2(2k-1), c=4
Discriminant (D)=b2-4ac
=[-2(2k-1)]2-4*k2*4
=4(4k2-4k+1)-16k2
=16k2-16k+4-16k2=-16k+4
Roots are real and equal
D=0
-16k+4=0⇒-16k=-4
k=4/16=1/4
k=1/4
(iii) (k + 1) x² – 2(k – 1) x + 1 = 0
Solution:
Here, a=k+1, b=-2(k-1) and c=1
Discriminant (D)=b2-4ac
=[-2(k-1)]2-4(k+1)*1
=4(k2-2k+1)-4(k+1)
=4k2-8k+4-4k-4=4k2-12k
Roots are real and equal
D=0
4k2-12k=0
k2-3k=0 ————-(Dividing by 4)
Either k=0
or k-3=0, then k=3
k=0,3
(iv) x² + k(2x + k – 1) + 2 = 0
Solution:
Here, a=1, b=2k, c=(k2-k+2)
Discriminant (D)=b2-4ac
=(2k)2-4*1*(k2-k+2)
=4k2-4k2+4k-8
=4k-8
Roots are real and equal
D=0
4k-8=0⇒k=2
Hence, k=2
Question 5. Find the values of k for which the following equations have real roots
(i) 2x² + kx + 3 = 0
Solution:
Here a = 2, b = k, c = 3
Roots are real and equal
D=0
k2-24=0⇒k2=24
k=±√24=±√4*6=±2√6
(ii) kx (x – 2) + 6 = 0
Solution:
kx2-2kx+6=0
here, a=k, b=-2k, c=6
Discriminant (D)=b2-4ac=(-2k)2-4*k*6=4k2-24k
Roots are real and equal
D=0
4k2-24k=0⇒4k(k-6)=0
k(k-6)=0
Either k=0 or
k-6=0, then k=6
k=0,6
(iii) x² – 4kx + k = 0
Solution:
Here, comparing with ax2+kx+c=0
a=1, b=-4k, c=k
Discriminant (D)=b2-4ac=(-4k)2-4*1*k=16k2-4k
Roots are real and equal
D=0
16k2-4k=0⇒4k(4k-1)=0
k(4k-1)=0
Either k=0
or 4k-1=0⇒4k=1
k=1/4, Hence k=0,1/4
(iv) kx(x – 2√5) + 10 = 0
Solution:
Here a=k, b=-2√5k, c=10
D=b2-4ac
=(-2√5k)2-4(k)(10)=20k2-40k
Roots are equal D=0
20k2-40k=0
k-2=0 ———(Dividing by 20k)
k=2
(v) kx (x – 3) + 9 = 0
Solution:
Here, a=k, b=-3k, c=9
D=b2-4ac
=(-3k)2-4(k)9
=9k2-36k
For roots to be real
D=0
9k2-36k=0
9k(k-4)=0
k-4=0⇒k=4
k=4
(vi) 4x² + kx + 3 = 0
Solution:
Here, a=4, b=k, c=3
D=b2-4ac
=k2-4(4)(3)
=k2-48
For roots to be real
D=0
k2-48=0
k2=48
k=±√48=±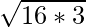
k=±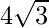
Question 6. Find the values of k for which the given quadratic equation has real and distinct roots :
(i) kx² + 2x + 1 = 0
Solution:
Here, a=k, b=2, c=1
D=b2-4ac
=(2)2-4*k*1
=4-4k
Roots are real and distinct
D>0⇒4-4k>0
1-k>0⇒1>k
⇒k<1
Therefore, k<1
(ii) kx² + 6x + 1 = 0
Solution:
Here, a=k, b=6, c=1
D=b2-4ac
=(6)2-4*k*1
=36-4k
Roots are real and distinct
D>0⇒36-4k>0
9-k>0⇒9>k
⇒k<9
Therefore, k<9
Question 7. For what value of k, (4 – k) x² + (2k + 4) x + (8k + 1) = 0, is a perfect square.
Solution:
(4 – k) x² + (2k + 4) x + (8k + 1) = 0
Here, a = 4 – k, b = 2k + 4, c = 8k + 1
=(2k+4)2-4*(4-k)(8k+1)
=4k2+16k+16-4(32k+4-8k2-k)
=4k2+16k+16-4(-8k2+31k+4)
=4k2+16k+16+32k2-124k-16
=36k2-108k
Therefore, the given quadratic equation is a perfect square
The roots are real and equal
D=0⇒36k2-108k=0
Either k=0
or k-3=0⇒k=3
k=0,3
Question 8. Find the least positive value of k for which the equation x² + kx + 4 = 0 has real roots.
Solution:
x² + kx + 4 = 0
Here, a=1, b=k, c=4
Therefore, Discriminant(D)=b2-4ac
=(k)2=4*1*4
=k2-16
It has real roots
D≥0⇒k2-16≥0
⇒k2≥16⇒(k)2≥(±4)2
k≥4 or k≤-4
Least positive value of k=4
Question 9. Find the value of k for which the quadratic equation (3k + 1) x² + 2(k + 1) x + 1 = 0 has equal roots. Also, find the roots.
Solution:
(3k + 1) x² + 2(k + 1) x + 1 = 0
Here a=(3k+1), b=2(k+1) ,c=1
Now, b2-4ac=[2(k+1)]2-4*(3k+1)*1
=4(k2+2k+1)-4(3k+1)
=4k2+8k+4-12k-4
=4k2-4k
Roots are real and equal
b2-4ac=0
4k2-4k=0
k2-k=0 k(k-1)=0
Either k=0 or k-1=0, then k=1
k=0,1
(i) When k=0, then
(3*0*1)x2+2(0+1)x+1=0
x2+2x+1=0
(x+1)2=0
x+1=0
x=-1
When k=1, then
(3*1+1)x2+2(1+1)x+1=0
4x2+4x2+1=0
(2x+1)2=0
2x+1=0
2x=-1⇒x=-1/2
x=1, -1/2
Question 10. Find the values of p for which the quadratic equation (2p + 1) x² – (7p + 2) x + (7p – 3) = 0 has equal roots. Also, find these roots.
Solution:
Here, a=2-+1, b=-(7p+2), c=(7p-3)
D=0 [Equal roots]
As b2-4ac=0
[-(7p+)]2-4(2p+1)(7p-3)=0
(7p+2)2-4(14p2-6p+7p-3)=0
49p2+28p+4-56p2+24p-28p+12=0
-7p2+24p+16=0
7p2-24-16=0 ————-(Dividing both sides by -1)
7p(p-4)+4(p-4)=0
(p-4)(7p+4)=0
p-4=0 or 7p+4=0
p=4 or p=-4/7
Roots are x=-b/2a [As equal roots (given)]
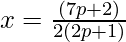
Where p=4,
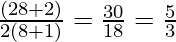
Equal roots is 5/3
When p=-4/7
![Rendered by QuickLaTeX.com x=\frac{[7(\frac{-4}{7})+2]}{[2(\frac{-4}{7}+1)]}\\ =\frac{\frac{(-28+14)}{7}}{2\frac{-8+7}{7}}=\frac{-14}{-2}=7](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2ddf41ae66e2d19f30d3b38e5d335802_l3.png)
Equal roots are 5/3 and 7
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...