The full form of HCF is the Highest Common Factor while the full form of LCM is the Least Common Multiple. HCF is the largest number that divides two or more numbers without leaving a remainder. LCM is the smallest multiple that is divisible by two or more integers.
Let’s learn about HCF and LCM in detail.
HCF and LCM Definition
HCF is the Highest Common Factor which can be seen in two or more numbers. It is denoted by HCF(a, b), where “a” and “b” are the numbers for which we want to find the highest common factor.
LCM can be seen in two or more numbers. It is denoted by LCM(a, b), where “a” and “b” are the numbers for which we want to find the least common multiple.
Let’s try to understand them better with the help of their definitions and examples.
HCF Definition
The HCF of two numbers is defined as the largest number that can exactly divide both the numbers.
HCF is the greatest common number that divides all the given numbers exactly. Therefore, HCF is also known as Greatest Common Divisor or GCD.
For an example, Let’s find the HCF of 6 and 18.
Solution:
Divisors of 6 = 1, 2, 3, 6
Divisors of 18 = 1, 2, 3, 6, 9, 18
HCF = greatest common divisor
HCF = 6
LCM Definition
The LCM of two or more numbers is defined as the smallest number that can be divided by all of the numbers.
LCM is the least number that is a common multiple of all the given numbers.
For an example, let’s find the LCM of 6 and 18.
Solution:
Multiple of 6 = 6, 12, 18, 24, 30, …
Multiple of 18 = 18, 36, 54, …
LCM = first common multiple (least common multiple)
LCM = 18
In order to find the HCF and LCM formula, let’s assume that the numbers given are a and b. The relationship between HCF and LCM states that the product of a and b is equal to the product of HCF and LCM.
(LCM of two numbers) × (HCF of two numbers) = Product of two numbers
Mathematically this can be written as:
LCM(a, b) × HCF(a, b) = a × b
How to Find HCF and LCM?
These are the most famous methods used to calculate HCF and LCM :
- Division method
- Prime factorization method
Let’s learn about all these methods in detail.
HCF by Division Method
The easiest way to understand how to find HCF by Division Method is by going back to simple division.
Following are the steps for better understanding this method :
Step 1: Take the smaller number as the divisor and the larger number as a dividend.
Step 2: Perform division. If you get the remainder as 0, then the divisor is the HCF of the given numbers.
Step 3: If you get a remainder other than 0 then take the remainder as the new divisor and the previous divisor as the new dividend.
Step 4: Perform steps 2 and step 3 until you get the remainder as 0.
Let’s try to understand this with the help of an example.
Example: Find out the HCF of 36 and 48.
Solution:
Using the division method for HCF
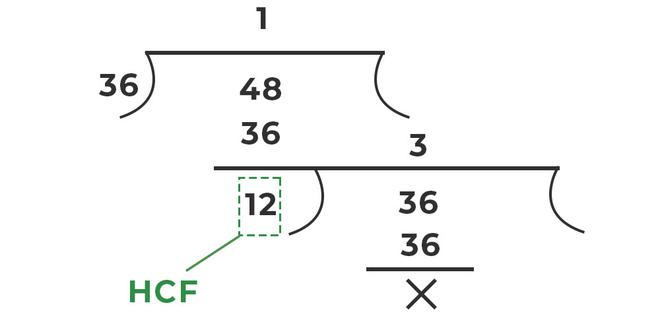
Hence, HCF = 12
LCM by Division Method
In order to find by Division method, we divide the
Following steps can be followed in order to find Least Common Division by Division Method:
Step 1: Check whether the given numbers are divisible by 2 or not.
Step 2: If the number is divisible by 2 then divide and again check for the same. If the numbers are not divisible by 2 then check 3, and so on.
Step 3: Perform step 2 until you get 1 in the end.
Example: Find out the LCM of 36 and 48.
Solution:
Using the division method for LCM

Hence, LCM = 2 × 2 × 2 × 2 × 3 × 3 × 3 = 432
Read More On LCM formula
HCF by Prime Factorization
Finding HCF by Prime Factorization can be done by following the given steps:
Step 1: Find out the prime factors of the given number.
Step 2: Check the occurrence of a particular factor. Find out the common factors and choose them in HCF.
Step 3: Multiply the occurrence of common factors. And this will be the HCF Of the given numbers.
Example: Find out the HCF of 18 and 90.
Solution:
Prime factors of 18 = 2 × 3 × 3
Prime factors of 90 = 2 × 3 × 3 × 5
Now, HCF = 2 × 3 × 3 = 18
LCM by Prime Factorization
Finding LCM by Prime Factorization is done by following the given steps:
Step 1: Find out the prime factors of the given number.
Step 2: Check the occurrence of a particular factor. If a particular factor has occurred multiple times in the given number, then choose the maximum occurrence of the factor in LCM. It can also be found out by checking the powers of the factors. The factor having greater power will be chosen between the numbers.
Step 3: Multiply all the maximum occurrences of a particular factor. And this will be the LCM Of the given numbers.
Example: Find out the LCM of 18 and 90.
Solution:
Prime factors of 18 = 2 × 3 × 3
Prime factors of 90 = 2 × 3 × 3 × 5
Now, LCM = 2 × 3 × 3 × 5 = 90
Alternate method:
Prime factors of 18 = 2 × 3 × 3
Prime factors of 18 = 21 × 32
Prime factors of 90 = 2 × 3 × 3 × 5
Prime factors of 90 = 21 × 32 × 51
Chosen factors for LCM = 21 × 32 × 51
Therefore, LCM = 2 × 9 × 5 = 90.
Read More,
Difference between HCF and LCM
Here are some key differences between HCF and LCM:
|
Feature
|
HCF
|
LCM
|
|
Abbreviation
|
It is the Highest Common Factor. |
It is the Least Common Multiple. |
|
Definition
|
The greatest of all the common factors among the given numbers is HCF. |
The smallest of all the common multiples among the given numbers is LCM. |
|
Properties
|
HCF is the largest number that divides two or more numbers without leaving a remainder.
|
LCM is the smallest multiple that is divisible by two or more integers.
|
|
Value Range
|
The HCF of given numbers will be always less than or equal to any of the numbers. |
The LCM of the given numbers will always be greater than or equal to any of the numbers given. |
|
Representation
|
Hcf(a,b) where “a” and “b” are two numbers.
|
Lcm(a,b) where “a” and “b” are two numbers.
|
|
Relation with Prime Numbers
|
It will involve the identification of common prime factors and multiplying them.
|
It involves identifying of all prime factors and multiplying maximum occurrence of each factor.
|
|
Application
|
Used in division, simplifying fractions, and problems involving factors and divisors
|
Used in multiplication, adding and subtracting fractions, and problems involving multiples and common intervals.
|
Read More,
HCF and LCM Examples
Let’s solve some sample questions on LCM and HCF now.
Example 1: Find out the LCM and HCF of 18, 30, and 90 by prime factorization.
Solution:
Prime factors of 18 = 2 × 3 × 3
Prime factors of 30 = 2 × 3 × 5
Prime factors of 90 = 2 × 3 × 3 × 5
LCM: 2 × 3 × 3 × 5 = 90
HCF: 2 × 3 = 6
Example 2: Find out the LCM and HCF of 318 and 504.
Solution:
Prime factors of 318 = 2 × 3 × 53
Prime factors of 504 = 2 × 2 × 2 × 3 × 3 × 7
LCM: 2 × 2 × 2 × 3 × 3 × 7 × 53
HCF: 2 × 3
Example 3: Find out the HCF of 24 and 36.
Solution:
Let’s find out the HCF of 24 and 36 by division method,

Therefore,
HCF = 2 × 2 × 3 = 12
Example 4: Find out the LCM of 24 and 36.
Solution:
Let’s find out the LCM pf 24 and 36 by division method,

Therefore,
LCM = 2 × 2 × 3 × 2 × 3 = 72
Example 4: Find out the LCM and HCF of 15 and 70. Also, verify the relationship between LCM, HCF, And given numbers.
Solution:
Prime factors of 15 = 3 × 5
Prime factors of 70 = 2 × 5 × 7
LCM: 2 × 3 × 5 × 7
HCF: 5
Verifying the relationship:
LCM × HCF = 2 × 3 × 5 × 5 × 7 = 1050
Product of two numbers = 15 × 70 = 1050
From above you can see that
LCM (15, 70) × HCF(15, 70) = Product of two numbers
Hence Verified.
HCF and LCM in Mathematics -FAQs
What is the full form of HCF and LCM.
The full form of HCF is the Highest Common Factor and the full form of LCM is the Lowest Common Multiple.
What is the formula of HCF and LCM?
The relationship between HCF and LCM states that the product of a and b is equal to the product of HCF and LCM.
(LCM of two numbers) × (HCF of two numbers) = Product of two numbers
This is written as:
LCM(a, b) × HCF(a, b) = a × b
What is GCF? Find GCF of 4 and 12.
GCF is the Greatest Common Factor which is nothing but another name for HCF.
GCF of 4 and 12 will be 4 as 4 is the greatest common factor between 4 and 12.
What are the different methods to find HCF and LCM in math?
There are various methods to find HCF and LCM. Following are the most famous methods used to calculate the Highest Common factor and Least Common Multiple:
- Division method
- Prime factorization method
What is the use of HCF and LCM?
HCF is very useful in mathematics and in real life as well. When numbers are required to be divided into smaller sections, or when certain things are required to be into smaller parts or in groups, HCF is used. LCM can be used in places where certain situations will require to occur multiple times.
Share your thoughts in the comments
Please Login to comment...