Class 10 NCERT Solutions- Chapter 4 Quadratic Equations – Exercise 4.4
Last Updated :
01 May, 2024
Question 1. Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
(i) 2x2-3x+5=0
(ii) 3x2-4√3x+4=0
(iii) 2x2-6x+3=0
Solution:
(i) Given: 2x2-3x+5=0
Here a=2,b=-3 and c=5
 Discriminant, D=b2-4ac
Discriminant, D=b2-4ac
= (-3)2– 4 × 2 × 5)
= 9-40 = -31 < 0
Hence, the roots are imaginary.
(ii) Given: 3x2-4√3x + 4 = 0
Here a=3,b=√3 and c=4
 Discriminant, D=b2-4ac
Discriminant, D=b2-4ac
= (-4√3)2 – (4 × 3 × 4)
= 48 – 48 = 0
Hence, the roots are real and equal.
Using the formula,
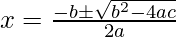 , we get
, we get
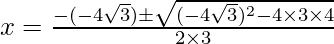
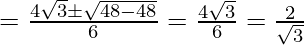
Hence, the equal roots are 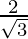 and
and 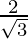 .
.
(iii) Given: 2x2-6x+3=0
Here, a=2,b=-6 and c=3
 Discriminant, D=b2-4ac
Discriminant, D=b2-4ac
= (-6)2 – (4 × 2 × 3)
= 36 – 24 = 12 > 0
Hence, the roots are distinct and real.
Using the formula,
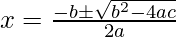 ,we get
,we get
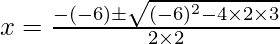
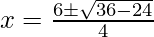
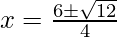
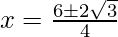
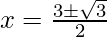
Hence, the equal roots are 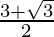 and
and 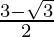
Question 2. Find the values of k for each of the following quadratic equations, so that they have two equal roots.
(i) 2x2+kx+3
(ii) kx(x-2)+6=0
Solution:
(i) 2x+kx+3=0
This equation is of the form ax2+bx+x, where a=2, b=k and c=3.
Discriminant, D=b2-4ac
=k2 – 4 × 2 × 3
=k2 -24
For equal roots D=0
 k2-24=0
k2-24=0
 k2=24
k2=24
 k2 = ±24 = ±2√6
k2 = ±24 = ±2√6
(ii) kx(x-2)+6=0
 kx2-2kx+6=0
kx2-2kx+6=0
This equation is of the form ax2+bx+c=0, where a=k, b=-2k and c=6.
Discriminant, D=b2-4ac
=(-2k)2 – 4 × k × 6
=4k2-24k
For equal roots D=0
 4k2-24k=0
4k2-24k=0
 4k(k-24)=0
4k(k-24)=0
 k=0 (not possible) or 4k-24=0
k=0 (not possible) or 4k-24=0
 k= 24/4=6
k= 24/4=6
Question 3. Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m2? If so, find its length and breadth.
Solution:
Let the breadth of the rectangular mango grove be x m.
Then, the length of the rectangular mango grove will be 2x m.
The Area of the rectangular mango grove=length × breadth
According to the question, we have
x × 2x= 800
 2x2=800
2x2=800
 x2=400
x2=400
 x=20
x=20
Hence, the rectangular mango grove is possible to design whose length=40 m and breadth=20 m.
Question 4. Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution:
Let the present age of one friend be x years.
Then, the present age of other friend be (20-x) years.
4 years ago, one friend’s age was (x-4) years
4 years ago, other friend’s age was (20-x-4)=(16-x) years.
According to the question,
(x-4)(16-x)=48
 16x-64-x2+4x=48
16x-64-x2+4x=48
 x2-20x+112=0
x2-20x+112=0
This equation is of the form ax2+bx+c=0,where a=1, b=-20 and c=112.
Discriminant, D=b2-4ac
= (-20)2-4 × 1 × 112 = -48 < 0
Since, there are no real roots.
So the given situation is not possible.
Question 5. Is it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so, find its length and breadth.
Solution:
Let the length of the rectangular park be x.
The perimeter of the rectangular park= 2(length + breadth)
 2(x + breadth)=80
2(x + breadth)=80
 breadth=40-x
breadth=40-x
The area of rectangular park= length × breadth
 x(40-x)=400
x(40-x)=400
\implies 40x-x2=400
\implies x2-40x+400=0
\implies x2 -20x-20x+400=0
 (x-20)(x-20)=0
(x-20)(x-20)=0
 x=20
x=20
Hence, the rectangular park is possible to design. So, the length of the park is 20m and the breadth = 40-20=20m.
Share your thoughts in the comments
Please Login to comment...