Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. The theorem can be expressed as r2 = p2 + q2, where ‘r’ is the hypotenuse and ‘p’ and ‘q’ are the two legs often called perpendicular and base of the triangle.
Pythagoras Theorem explains the relationship between the three sides of a right-angled triangle and helps us find the length of a missing side if the other two sides are known. It is also known as Pythagorean theorem.
Let’s learn about the Pythagoras theorem statement, its formula, proof, and examples in detail.
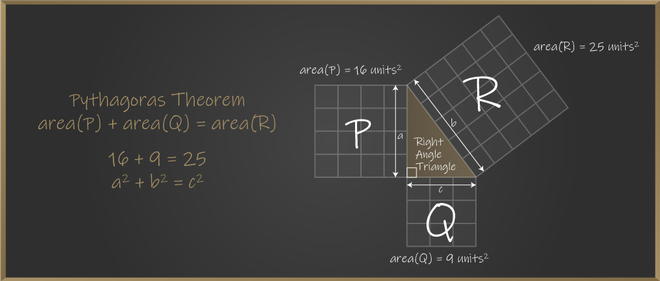
Pythagoras Theorem Statement
The Pythagoras Theorem states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. It provides us with the relationship between the sides in a right-angled triangle. A right triangle consists of two legs and a hypotenuse.
Pythagoras theorem formula is AC2 = AB2 + BC2, where AB is the perpendicular side, BC is the base, and AC is the hypotenuse side. The Pythagoras equation is applied to any triangle that has one of its angles equal to 90°.
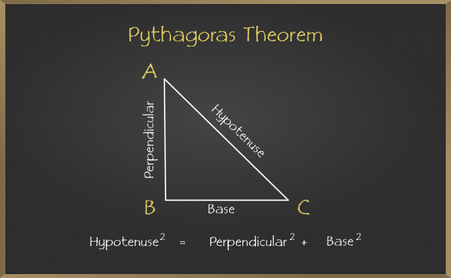
Pythagoras Formula
The three sides of the right-angled triangle are called the Pythagoras Triplets.
Pythagoras Theorem Proof
Consider a right-angled triangle having sides A, B, and C. Here, AC is the longest side (hypotenuse), and AB and BC are the legs of the triangle. Draw a perpendicular line BD at AC as shown in the figure below,
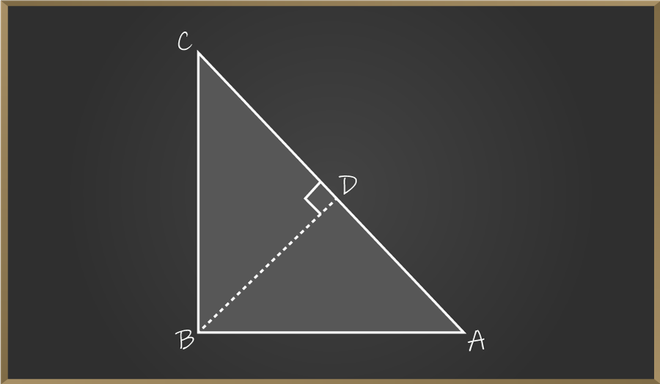
Derivation of Pythagoras Theorem
In △ABD and △ACB,
∠A = ∠A (Common angle)
∠ADB = ∠ABC (90°)
Therefore, we can say △ABD ∼ △ ACB (By AA Similarity)
Similarly, △BDC ∼ △ACB
Hence, AD/AB = AB/AC
AB2 = AD × AC ⇢ (1)
And, CD/BC = BC/AC
BC2 = CD × AC ⇢ (2)
Adding equations (1) and (2),
AB2 + BC2 = AC × AD + AC × CD
AB2 + BC2 = AC (AD + CD)
AB2 + BC2 = AC × AC
AB2 + BC2 = AC2
Also, AC2 = AB2 + BC2
Hence proved.
Converse of Pythagoras Theorem
The converse of the Pythagoras theorem states that,
If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
Converse of Pythagoras Theorem Proof
For a triangle with the length of its sides a, b, if c2 = a2 + b2, we need to prove that the triangle is right-angled.
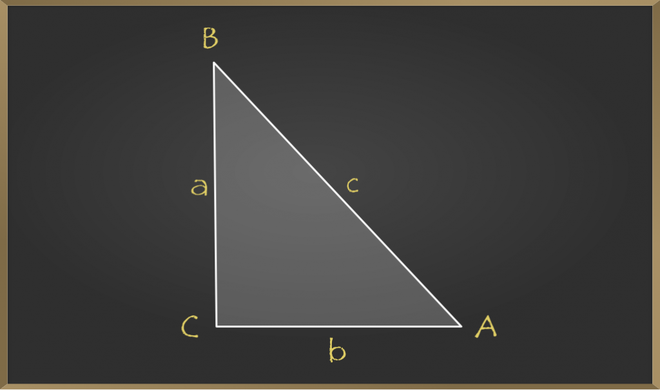
We assume that it satisfies c2 = a2 + b2, and by looking into the diagram, we can tell that ∠C = 90°, but to prove it, we require another triangle △EGF, such as AC = EG = b and BC = FG = a.
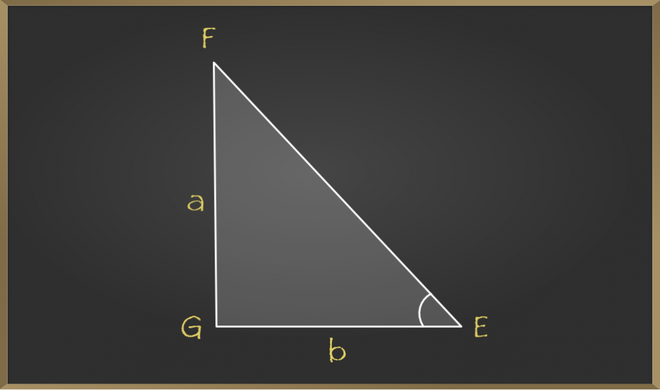
In △EGF, by Pythagoras Theorem:
⇒ EF2 = EG2 + FG22 = b2 + a2 ⇢ (1)
In △ABC, by Pythagoras Theorem:
⇒ AB2 = AC2 + BC2 = b2 + a2 ⇢ (2)
From equation (1) and (2), we have;
⇒ EF2 = AB2
⇒ EF = AB
⇒ △ ACB ≅ △EGF (By SSS postulate)
⇒ ∠G is right angle
Thus, △EGF is a right triangle. Hence, we can say that the converse of the Pythagorean theorem also holds.
History of Pythagoras Theorem
The history of the Pythagoras Theorem goes back to the ancient Babylon and Egypt eras. It is named after the ancient Greek mathematician and philosopher Pythagoras of Samos. He lived during the 6th century BCE.
But the roots of this theorem go to ancient cultures. It is very likely that Babylonians and Indians used this theorem well before Pythagoras, but its widespread use came into existence after Pythagoras stated it. The Pythagorean theorem is also known as the Baudhayana theorem, listed in the book Baudhāyana Śulbasûtra by the great Indian mathematician Baudhāyana.
One of the other reasons this theorem is known as Pythagoras or Pythagorean Theorem is because the disciples of Pythagoras spread knowledge and philosophy of Pythagoras after his death as well.
Pythagoras Theorem Applications
Below are some of the uses of Pythagorean Theorem in real life:
- The Pythagoras theorem is used for navigation in order to find the shortest distance, etc.
- In order to recognize faces in security cameras, this theorem is required to understand the distance of the person from the camera.
- In engineering fields, it is used to calculate the unknown dimension, say, the diameter of a particular sector.
Related Articles:
Solved Examples on Pythagoras Theorem
Let’s solve some questions on Pythagoras Theorem.
Example 1: In the below given right triangle, find the value of y.
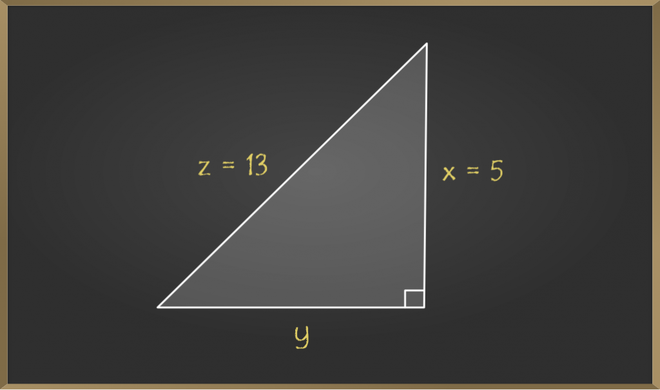
Solution:
By the statement of the Pythagoras theorem we get,
⇒ z2 = x2 + y2
Now, substituting the values directly we get,
⇒ 132 = 52 + y2
⇒ 169 = 25 + y2
⇒ y2 = 144
⇒ y = √144 = 12
Example 2: Given a rectangle with a length of 4 cm and breadth of 3 cm. Find the length of the diagonal of the rectangle.
Solution:

In the above diagram length of the rectangle is 4 cm, and the width is 3 cm. Now we have to find the distance between point A to point C or point B to point D. Both give us the same answer because opposite sides are of the same length i.e., AC = BD. Now let’s find the distance between points A and C by drawing an imaginary line.
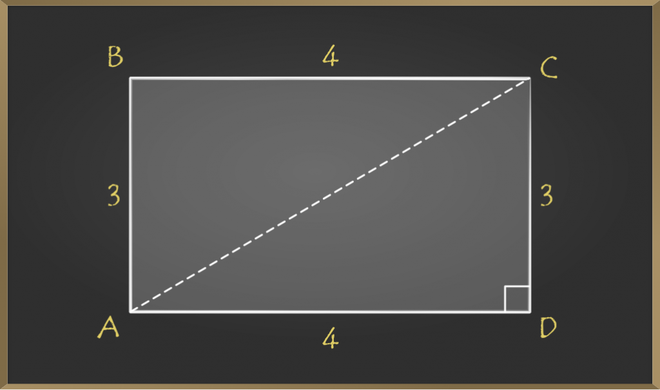
Now triangle ACD is a right triangle.
So by the statement of Pythagoras theorem,
⇒ AC2 = AD2 + CD2
⇒ AC2 = 42 + 32
⇒ AC2 = 25
⇒ AC = √25 = 5
Therefore length of the diagonal of given rectangle is 5 cm.
Example 3: The sides of a triangle are 5, 12, and 13. Check whether the given triangle is a right triangle or not.
Solution:
Given,
⇒ a = 5
⇒ b = 12
⇒ c = 13
By using the converse of Pythagorean Theorem,
⇒ a2 + b2 = c2
Substitute the given values in the above equation,
⇒ 132 = 52 + 122
⇒ 169 = 25 + 144
⇒ 169 = 169
So, the given lengths satisfy the above condition.
Therefore, the given triangle is a right triangle.
Example 4: The side of a triangle is of lengths 9 cm, 11 cm, and 6 cm. Is this triangle a right triangle? If so, which side is the hypotenuse?
Solution:
We know that hypotenuse is the longest side. If 9 cm, 11 cm, and 6 cm are the lengths of the angled triangle, then 11 cm will be the hypotenuse.
Using the converse of Pythagoras theorem, we get
⇒ (11)2 = (9)2 + (6)2
⇒ 121 = 81 + 36
⇒ 121 ≠ 117
Since, both the sides are not equal therefore 9 cm, 11 cm and 6 cm are not the side of the right-angled triangle.
Pythagoras Theorem Questions
Here are some practice questions on the Pythagoras theorem for you to solve.
Q1: If the two shorter sides of a right angled triangle measures 14 and 15 cm, find the length of the longest side.
Q2: If the hypotenuse and perpendicular of a right angled triangle are 5 and 4 cm then find the base.
Q3: In a triangular field the sides measures 24 cm, 7 cm and 25 cm then prove that field is the form of a right triangle.
Q4: A wall is of 12 m height and a ladder of 13 m is placed against it touching its top. Find the distance between the foot of the ladder and the wall.
Pythagorean Theorem- FAQs
State Pythagoras Theorem.
Pythagoras theorem states that, the square of the hypotenuse is equal to the sum of the sides of the perpendicular and base. It can be written as:
c2 = a2 + b2
Who invented Pythagoras Theorem?
Greek mathematician and philosopher Pythagoras of Samos (commonly known as Pythagoras) is credited with the invention of Pythagoras’ Theorem. Scientists also found inscriptions of the same theorem in the ruins of ancient Egypt and Babylon, but their use of the theorem was not widely publicized until Pythagoras stated it.
What is Pythagoras Theorem Formula?
Pythagorean theorem formula is: a2 + b2 = c2 , where “a” and “b” represent the lengths of the two shorter sides of the right triangle and “c” represents the “hypotenuse.”
What is Converse of Pythagoras Theorem?
The converse of Pythagoras theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
Can we apply Pythagoras Theorem to any triangle?
No, we can apply the Pythagoras theorem to the right-angled triangles only.
What are applications of Pythagoras Theorem?
Applications of the Pythagoras theorem are in various fields:
- Architecture and navigation site.
- In order to calculate the surface area and volume, etc.
Share your thoughts in the comments
Please Login to comment...