Finding the vertex, focus and directrix of a parabola
Last Updated :
22 Jun, 2022
Problem – Find the vertex, focus and directrix of a parabola when the coefficients of its equation are given.
A set of points on a plain surface that forms a curve such that any point on that curve is equidistant from the focus is a parabola.
Vertex of a parabola is the coordinate from which it takes the sharpest turn whereas a is the straight line used to generate the curve.
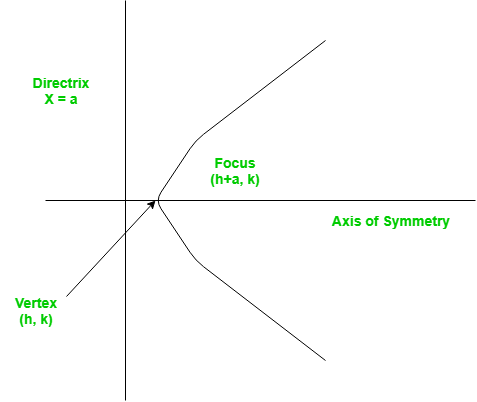
The standard form of a parabola equation is 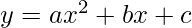 . Given the values of a, b and c; our task is to find the coordinates of vertex, focus and the equation of the directrix.
. Given the values of a, b and c; our task is to find the coordinates of vertex, focus and the equation of the directrix.
Example –
Input : 5 3 2
Output : Vertex:(-0.3, 1.55)
Focus: (-0.3, 1.6)
Directrix: y=-198
Consult the formula below for explanation.
This problem is a simple example of implementations of formulae. Given below are the required set of formulae which will help us tackle the problem.
For a parabola in the form 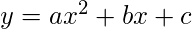 Vertex:
Vertex: 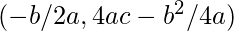 Focus:
Focus: 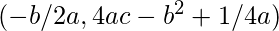 Directrix:
Directrix: 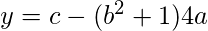
C++
#include <iostream>
using namespace std;
void parabola(float a, float b, float c)
{
cout << "Vertex: (" << (-b / (2 * a)) << ", "
<< (((4 * a * c) - (b * b)) / (4 * a))
<< ")" << endl;
cout << "Focus: (" << (-b / (2 * a)) << ", "
<< (((4 * a * c) - (b * b) + 1) / (4 * a))
<< ")" << endl;
cout << "Directrix: y="
<< c - ((b * b) + 1) * 4 * a << endl;
}
int main()
{
float a = 5, b = 3, c = 2;
parabola(a, b, c);
return 0;
}
|
Java
class GFG {
static void parabola(float a,
float b, float c)
{
System.out.println("Vertex: (" +
(-b / (2 * a)) + ", " +
(((4 * a * c) - (b * b)) /
(4 * a)) + ")");
System.out.println("Focus: (" +
(-b / (2 * a)) + ", " +
(((4 * a * c) - (b * b) + 1) /
(4 * a)) + ")");
System.out.println("Directrix:" + " y=" +
(int)(c - ((b * b) + 1) *
4 * a));
}
public static void main(String[] args)
{
float a = 5, b = 3, c = 2;
parabola(a, b, c);
}
}
|
Python 3
def parabola(a, b, c):
print("Vertex: (" , (-b / (2 * a)),
", ", (((4 * a * c) - (b * b))
/ (4 * a)), ")", sep = "")
print("Focus: (" , (-b / (2 * a)),
", ", (((4 * a * c) - (b * b) + 1)
/ (4 * a)), ")", sep = "")
print("Directrix: y=", c - ((b * b)
+ 1) * 4 * a, sep = "")
a = 5
b = 3
c = 2
parabola(a, b, c)
|
C#
using System;
class GFG {
static void parabola(float a,
float b, float c)
{
Console.WriteLine("Vertex: (" +
(-b / (2 * a)) + ", " +
(((4 * a * c) - (b * b)) /
(4 * a)) + ")");
Console.WriteLine("Focus: (" +
(-b / (2 * a)) + ", " +
(((4 * a * c) - (b * b) + 1) /
(4 * a)) + ")");
Console.Write("Directrix:" + " y=" +
(int)(c - ((b * b) + 1) * 4 * a));
}
public static void Main()
{
float a = 5, b = 3, c = 2;
parabola(a, b, c);
}
}
|
PHP
<?php
function parabola($a, $b, $c)
{
echo "Vertex: (" , (-$b / (2 * $a)) , ", ",
(((4 * $a * $c) - ($b * $b)) / (4 * $a)),
")", "\n" ;
echo "Focus: (" , (-$b / (2 * $a)) , ", ",
(((4 * $a * $c) - ($b * $b) + 1) / (4 * $a))
, ")"," \n" ;
echo "Directrix: y=",
$c - (($b * $b) + 1) * 4 * $a ;
}
$a = 5; $b = 3; $c = 2;
parabola($a, $b, $c);
?>
|
Javascript
<script>
function parabola(a, b, c)
{
document.write("Vertex: (" +
(-b / (2 * a)) + ", " +
(((4 * a * c) - (b * b)) /
(4 * a)) + ")" + "<br/>");
document.write("Focus: (" +
(-b / (2 * a)) + ", " +
(((4 * a * c) - (b * b) + 1) /
(4 * a)) + ")" + "<br/>");
document.write("Directrix:" + " y=" +
(c - ((b * b) + 1) *
4 * a) + "<br/>");
}
let a = 5, b = 3, c = 2;
parabola(a, b, c);
</script>
|
Output –
Vertex:(-0.3, 1.55)
Focus: (-0.3, 1.6)
Directrix: y=-198
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...