Program to find area of a Circular Segment

In a circle, if a chord is drawn then that chord divides the whole circle into two parts. These two parts of the circle are called segments of the circle. The smaller area is known as the Minor segment and the larger area is called as the Major segment.
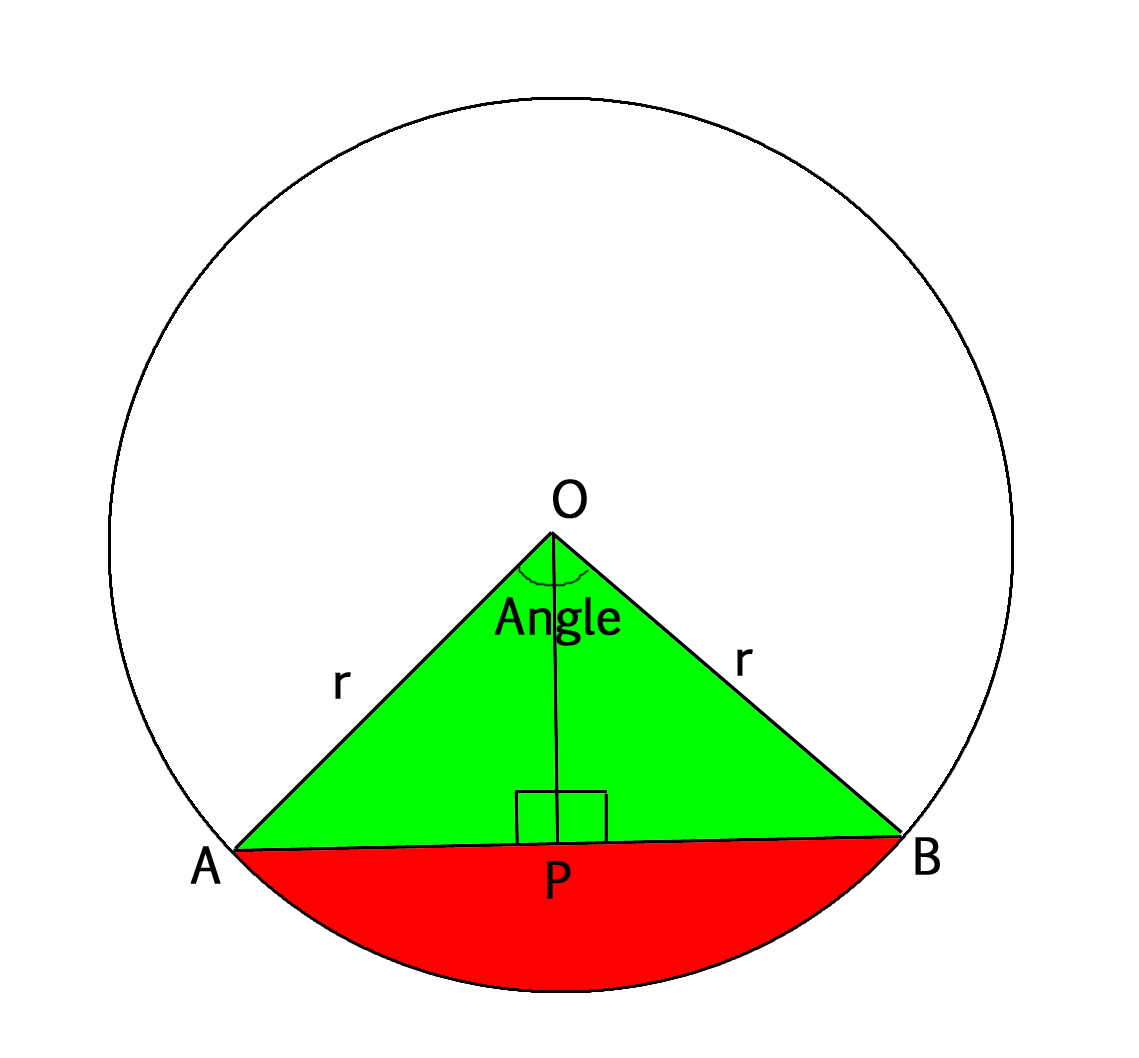
In the figure below, the chord AB divides the circle into minor and major segments. 

We are given radius of circle and angle that forms minor segment. We need to find areas of two segments.
Examples : 

Input : 
radius = 21.0
angle = 120.0
Output :
Area of minor segment 270.855
Area of major segment 1114.59

Input :
radius = 10.0
angle = 90.0
Output : 
Area of minor segment 28.5397
Area of major segment 285.619

Area of the segment :

For that, we join the end points of the chord with the center of the circle resulting in a sector which subtends some ‘angle’ at the center. And a perpendicular is drawn from the center of the circle on the chord AB. By congruence of triangles, we obtain that the ∠ AOP = ∠ BOP = 1/2(angle). 

Formula for Area of Segment :

Area of Segment = Area of sector - Area of Triangle OAB 
                = pi * r2 * (angle/360) -
                  Area of Triangle OAB

For detailed information about formula of Area of Sector, refer https://www.geeksforgeeks.org/area-of-a-sector/. 

In the figure above, assume angle made by sector = X,
so ∠ AOP = ∠ BOP = X/2

Area of Triangle AOB = 1/2 * base * height
                     = 1/2 * AB * OP

Now in Triangle AOP, By trigonometry
Cos(X/2) = OP/AO  i.e. OP = AO * Cos(X/2) 
                       OP = r * Cos(X/2)
Sin(X/2) = AP/AO  i.e. AP = AO * Sin(X/2) 
                       AP = r * Sin(X/2)

So,
Base = AB = AP + PB
          = 2 * AP
          = 2 * r * Sin(X/2)
   
Height = OP = r * Cos(X/2)

Area of triangle = 1/2 * (2 * r * Sin(X/2)) * (r * Cos(X/2))
                    = 1/2 * r2 * Sin(X) 
                      [Using identity 2 * Sin(A) * Cos(A)]
                    = Sin(2 * A))

Hence Area of Segment =  pi * r2 * (angle/360) - 1/2 * r2 * Sin(angle)

C++

// C++ Program to
// find area of
// segment of a
// circle
#include <bits/stdc++.h>
using namespace std;

float pi = 3.14159;

// Function to find
// area of segment
float area_of_segment(float radius,
                      float angle)
{
    // Calculating area of sector
    float area_of_sector = pi *
                           (radius * radius)
                           *(angle / 360);

    // Calculating area of triangle
    float area_of_triangle = (float)1 / 2 *
                             (radius * radius) *
                             sin((angle * pi) / 180);

    return area_of_sector - area_of_triangle;
}

// Driver Code
int main()
{
    float radius = 10.0, angle = 90.0;
    cout << "Area of minor segment = "
        << area_of_segment(radius, angle) << endl;

    cout << "Area of major segment = "
        << area_of_segment(radius, (360 - angle));
}

Java

// Java Program to find area of
// segment of a circle
class GFG {
static float pi = 3.14159f;

static float area_of_segment(float radius,
                              float angle)
{
    // Calculating area of sector
    float area_of_sector = pi *
   (radius * radius) * (angle / 360);

    // Calculating area of triangle
    float area_of_triangle =
        (float)1 / 2 * (radius * radius) *
        (float)Math.sin((angle * pi) / 180);

    return area_of_sector - area_of_triangle;
}

// Driver Function
public static void main(String[] args)
{
    float radius = 10.0f, angle = 90.0f;
    System.out.println("Area of minor segment = " +
                    area_of_segment(radius, angle));

    System.out.println("Area of major segment = " +
                    area_of_segment(radius, (360 - angle)));
}
}

// This code is contributed by Anant Agarwal.

Python

# Python3 Program
# to find area of
# segment of a
# circle
import math

pi = 3.14159

# Function to find
# area of segment
def area_of_segment(radius, angle):
    # Calculating area of sector
    area_of_sector = pi *
                     (radius * radius)
                     * (angle / 360)

    # Calculating area of triangle
    area_of_triangle = 1 / 2 *
                       (radius * radius) *
                       math.sin((angle * pi) / 180)

    return area_of_sector - area_of_triangle;


# Driver Code
radius = 10.0
angle = 90.0
print("Area of minor segment =",
       area_of_segment(radius, angle))
print("Area of major segment =",
      area_of_segment(radius, (360 - angle)))


# This code is contributed by Smitha Dinesh Semwal

C#

// C# Program to find area
// of segment of a circle
using System;

class GFG {
      static float pi = 3.14159f;

      static float area_of_segment(float radius,
                                   float angle)
{
    // Calculating area of sector
    float area_of_sector = pi * (radius * radius)
                             * (angle / 360);

    // Calculating area of triangle
    float area_of_triangle =(float)1 / 2 * (radius * radius)
                            *(float)Math.Sin((angle * pi) / 180);

    return area_of_sector - area_of_triangle;
}

    // Driver Function
    public static void Main()
{
    float radius = 10.0f, angle = 90.0f;
    Console.WriteLine("Area of minor segment = " +
                        area_of_segment(radius, angle));

    Console.WriteLine("Area of major segment = " +
                       area_of_segment(radius, (360 - angle)));
}
}

// This code is contributed by vt_m.

PHP

<?php
// PHP Program to
// find area of
// segment of a
// circle

// Function to find
// area of segment
function area_of_segment($radius,
                          $angle)

{
    $pi = 3.14159;

    // Calculating area of sector
    $area_of_sector = $pi * ($radius * $radius) *
                                   ($angle / 360);

    // Calculating area of triangle
    $area_of_triangle = 1 / 2 *    ($radius * $radius)
                              * sin(($angle * $pi) / 180);

    return $area_of_sector - $area_of_triangle;
}

    // Driver Code
    $radius = 10.0;
    $angle = 90.0;
    echo ("Area of minor segment = ");
    echo( area_of_segment($radius, $angle));
    echo("\n");

    echo("Area of major segment = ");
    echo(area_of_segment($radius, (360 - $angle)));

// This code is contributed by vt_m.
?>

Javascript

<script>

// javascript program to find area of
// segment of a circle
let pi = 3.14159;

function area_of_segment(radius,
                              angle)
{
    // Calculating area of sector
    let area_of_sector = pi *
   (radius * radius) * (angle / 360);

    // Calculating area of triangle
    let area_of_triangle =
        1 / 2 * (radius * radius) *
        Math.sin((angle * pi) / 180);

    return area_of_sector - area_of_triangle;
}


// Driver Function

         let radius = 10.0, angle = 90.0;
    document.write("Area of minor segment = " +
                    area_of_segment(radius, angle) + "<br/>");

    document.write("Area of major segment = " +
                    area_of_segment(radius, (360 - angle)));

    // This code is contributed by jana_sayantan.
</script>

Output : 

Area of minor segment = 28.5397
Area of major segment = 285.619

Time Complexity: O(1) 
Auxiliary Space: O(1)

Please suggest if someone has a better solution which is more efficient in terms of space and time.
This article is contributed by Aarti_Rathi. Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above