Find Simple Closed Path for a given set of points

Given a set of points, connect the dots without crossing. 

Example: 

Input: points[] = {(0, 3), (1, 1), (2, 2), (4, 4),
                   (0, 0), (1, 2), (3, 1}, {3, 3}};

Output: Connecting points in following order would
        not cause any crossing
       {(0, 0), (3, 1), (1, 1), (2, 2), (3, 3),
        (4, 4), (1, 2), (0, 3)}

We strongly recommend you to minimize your browser and try this yourself first.
The idea is to use sorting. 

• Find the bottom-most point by comparing y coordinate of all points. If there are two points with same y value, then the point with smaller x coordinate value is considered. Put the bottom-most point at first position. 
  

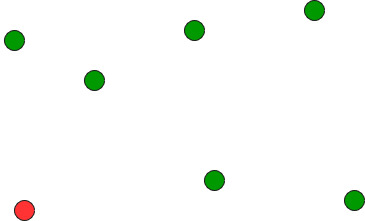
• Consider the remaining n-1 points and sort them by polar angle in counterclockwise order around points[0]. If polar angle of two points is same, then put the nearest point first.
• Traversing the sorted array (sorted in increasing order of angle) yields simple closed path. 
  

How to compute angles?
One solution is to use trigonometric functions. 
Observation: We don’t care about the actual values of the angles. We just want to sort by angle. 
Idea: Use the orientation to compare angles without actually computing them!

Below is C++ implementation of above idea.  

C++

// A C++ program to find simple closed path for n points
// for explanation of orientation()
#include <bits/stdc++.h>
using namespace std;

struct Point
{
    int x, y;
};

// A global point needed for  sorting points with reference
// to the first point. Used in compare function of qsort()
Point p0;

// A utility function to swap two points
int swap(Point &p1, Point &p2)
{
    Point temp = p1;
    p1 = p2;
    p2 = temp;
}

// A utility function to return square of distance between
// p1 and p2
int dist(Point p1, Point p2)
{
    return (p1.x - p2.x)*(p1.x - p2.x) +
           (p1.y - p2.y)*(p1.y - p2.y);
}

// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are collinear
// 1 --> Clockwise
// 2 --> Counterclockwise
int orientation(Point p, Point q, Point r)
{
    int val = (q.y - p.y) * (r.x - q.x) -
              (q.x - p.x) * (r.y - q.y);

    if (val == 0) return 0;  // collinear
    return (val > 0)? 1: 2; // clockwise or counterclock wise
}

// A function used by library function qsort() to sort
//  an array of points with respect to the first point
int compare(const void *vp1, const void *vp2)
{
   Point *p1 = (Point *)vp1;
   Point *p2 = (Point *)vp2;

   // Find orientation
   int o = orientation(p0, *p1, *p2);
   if (o == 0)
     return (dist(p0, *p2) >= dist(p0, *p1))? -1 : 1;

   return (o == 2)? -1: 1;
}

// Prints simple closed path for a set of n points.
void printClosedPath(Point points[], int n)
{
   // Find the bottommost point
   int ymin = points[0].y, min = 0;
   for (int i = 1; i < n; i++)
   {
     int y = points[i].y;

     // Pick the bottom-most. In case of tie, choose the
     // left most point
     if ((y < ymin) || (ymin == y &&
         points[i].x < points[min].x))
        ymin = points[i].y, min = i;
   }

   // Place the bottom-most point at first position
   swap(points[0], points[min]);

   // Sort n-1 points with respect to the first point.
   // A point p1 comes before p2 in sorted output if p2
   // has larger polar angle (in counterclockwise
   // direction) than p1
   p0 = points[0];
   qsort(&points[1], n-1, sizeof(Point), compare);

   // Now stack has the output points, print contents
   // of stack
   for (int i=0; i<n; i++)
       cout << "(" << points[i].x << ", "
            << points[i].y <<"), ";
}

// Driver program to test above functions
int main()
{
    Point points[] = {{0, 3}, {1, 1}, {2, 2}, {4, 4},
                       {0, 0}, {1, 2}, {3, 1}, {3, 3}};
    int n = sizeof(points)/sizeof(points[0]);
    printClosedPath(points, n);
    return 0;
}

Java

import java.util.*;

class Point {
    int x, y;
    Point(int x, int y) {
        this.x = x;
        this.y = y;
    }
}

class ConvexHull {
    static Point p0;

    static void swap(Point p1, Point p2) {
        Point temp = p1;
        p1 = p2;
        p2 = temp;
    }

    static int dist(Point p1, Point p2) {
        return (int)Math.pow(p1.x - p2.x, 2) +
               (int)Math.pow(p1.y - p2.y, 2);
    }

    static int orientation(Point p, Point q, Point r) {
        int val = (q.y - p.y) * (r.x - q.x) -
                  (q.x - p.x) * (r.y - q.y);

        if (val == 0) return 0; // collinear
        return (val > 0)? 1: 2;
    }

    static int compare(Point p1, Point p2) {
        int o = orientation(p0, p1, p2);
        if (o == 0)
            return (dist(p0, p2) >= dist(p0, p1))? -1 : 1;
        return (o == 2)? -1: 1;
    }

    static void printClosedPath(Point points[], int n) {
        int ymin = points[0].y, min = 0;
        for (int i = 1; i < n; i++) {
            int y = points[i].y;
            if ((y < ymin) || (ymin == y &&
                points[i].x < points[min].x))
                ymin = points[i].y;
                min = i;
        }
        swap(points[0], points[min]);
        p0 = points[0];
        Arrays.sort(points, 1, n, (p1, p2) -> compare(p1, p2));
        for (int i=0; i<n; i++)
            System.out.println("(" + points[i].x + ", " + points[i].y + "), ");
    }

    public static void main(String[] args) {
        Point[] points = {new Point(0, 3), new Point(1, 1), new Point(2, 2), new Point(4, 4),
                          new Point(0, 0), new Point(1, 2), new Point(3, 1), new Point(3, 3)};
        int n = points.length;
        printClosedPath(points, n);
    }
}

Python3

from functools import cmp_to_key
# A Python program to find simple closed path for n points
# for explanation of orientation()

# A global point needed for  sorting points with reference
# to the first point. Used in compare function of qsort()
p0 = None

# A utility function to return square of distance between
# p1 and p2
def dist(p1, p2):
    return (p1[0] - p2[0])*(p1[0] - p2[0]) + (p1[1] - p2[1])*(p1[1] - p2[1])

# To find orientation of ordered triplet (p, q, r).
# The function returns following values
# 0 --> p, q and r are collinear
# 1 --> Clockwise
# 2 --> Counterclockwise
def orientation(p, q, r):
    val = (q[1] - p[1]) * (r[0] - q[0]) - (q[0] - p[0]) * (r[1] - q[1])

    if val == 0: return 0  # collinear
    return 1 if val > 0 else 2 # clockwise or counterclock wise

# A function used by library function qsort() to sort
#  an array of points with respect to the first point
def compare(vp1, vp2):
    p1 = vp1
    p2 = vp2

    # Find orientation
    o = orientation(p0, p1, p2)
    if o == 0:
        return -1 if dist(p0, p2) >= dist(p0, p1) else 1

    return -1 if o == 2 else 1

# Prints simple closed path for a set of n points.
def printClosedPath(points, n):
    global p0
    # Find the bottommost point
    ymin = points[0][1]
    min = 0
    for i in range(1,n):
        y = points[i][1]

        # Pick the bottom-most. In case of tie, choose the
        # left most point
        if (y < ymin) or (ymin == y and points[i][0] < points[min][0]):
            ymin = points[i][1]
            min = i

    # Place the bottom-most point at first position
    temp = points[0]
    points[0] = points[min]
    points[min] = temp

    # Sort n-1 points with respect to the first point.
    # A point p1 comes before p2 in sorted output if p2
    # has larger polar angle (in counterclockwise
    # direction) than p1
    p0 = points[0]
    points.sort(key=cmp_to_key(compare))

    # Now stack has the output points, print contents
    # of stack
    for i in range(n):
        print("(",points[i][0],",",points[i][1],"), ", end="")

# Driver program to test above functions
points = [[0, 3], [1, 1], [2, 2], [4, 4], [0, 0], [1, 2], [3, 1], [3, 3]]
n = len(points)

printClosedPath(points, n)

C#

using System;
using System.Collections.Generic;

public class Point {
    public int x, y;
    public Point(int x, int y)
    {
        this.x = x;
        this.y = y;
    }
}

public class ClosestPath {
    static Point p0;

    static int dist(Point p1, Point p2)
    {
        return (p1.x - p2.x) * (p1.x - p2.x)
            + (p1.y - p2.y) * (p1.y - p2.y);
    }

    static int orientation(Point p, Point q, Point r)
    {
        int val = (q.y - p.y) * (r.x - q.x)
                  - (q.x - p.x) * (r.y - q.y);
        if (val == 0)
            return 0; // collinear
        return (val > 0)
            ? 1
            : 2; // clockwise or counterclockwise
    }

    static int compare(Point p1, Point p2)
    {
        int o = orientation(p0, p1, p2);
        if (o == 0)
            return (dist(p0, p2) >= dist(p0, p1)) ? -1 : 1;
        return (o == 2) ? -1 : 1;
    }

    static void printClosedPath(List<Point> points, int n)
    {
        // Find the bottommost point
        int ymin = points[0].y;
        int min = 0;
        for (int i = 1; i < n; i++) {
            int y = points[i].y;
            if ((y < ymin)
                || (ymin == y
                    && points[i].x < points[min].x)) {
                ymin = points[i].y;
                min = i;
            }
        }

        // Place the bottom-most point at first position
        Point temp = points[0];
        points[0] = points[min];
        points[min] = temp;

        // Sort n-1 points with respect to the first point.
        // A point p1 comes before p2 in sorted output if p2
        // has larger polar angle (in counterclockwise
        // direction) than p1
        p0 = points[0];
        points.Sort(compare);

        // Now stack has the output points, print contents
        // of stack
        for (int i = 0; i < n; i++) {
            Console.Write("(" + points[i].x + ", "
                          + points[i].y + "), ");
        }
    }

    public static void Main()
    {
        List<Point> points = new List<Point>() {
            new Point(0, 3), new Point(1, 1),
                new Point(2, 2), new Point(4, 4),
                new Point(0, 0), new Point(1, 2),
                new Point(3, 1), new Point(3, 3)
        };
        int n = points.Count;

        printClosedPath(points, n);
    }
}
// This code is contributed by user_dtewbxkn77n

Javascript

// A javascript program to find simple closed path for n points
// for explanation of orientation()

// A global point needed for  sorting points with reference
// to the first point. Used in compare function of qsort()
let p0;

// A utility function to return square of distance between
// p1 and p2
function dist(p1, p2)
{
    return (p1[0] - p2[0])*(p1[0] - p2[0]) +
           (p1[1] - p2[1])*(p1[1] - p2[1]);
}

// To find orientation of ordered triplet (p, q, r).
// The function returns following values
// 0 --> p, q and r are collinear
// 1 --> Clockwise
// 2 --> Counterclockwise
function orientation(p, q, r)
{
    let val = (q[1] - p[1]) * (r[0] - q[0]) - (q[0] - p[0]) * (r[1] - q[1]);

    if (val == 0) return 0;  // collinear
    return (val > 0)? 1: 2; // clockwise or counterclock wise
}

// A function used by library function qsort() to sort
//  an array of points with respect to the first point
function compare(vp1, vp2)
{
   let p1 = vp1;
   let p2 = vp2;

   // Find orientation
   let o = orientation(p0, p1, p2);
   if (o == 0)
     return (dist(p0, p2) >= dist(p0, p1))? -1 : 1;

   return (o == 2)? -1: 1;
}

// Prints simple closed path for a set of n points.
function printClosedPath(points, n)
{
   // Find the bottommost point
   let ymin = points[0][1];
   let min = 0;
   for (let i = 1; i < n; i++)
   {
     let y = points[i][1];

     // Pick the bottom-most. In case of tie, choose the
     // left most point
     if ((y < ymin) || (ymin == y && points[i][0] < points[min][0])){
        ymin = points[i][1];
        min = i;
     }

   }

   // Place the bottom-most point at first position
   let temp = points[0];
    points[0] = points[min];
    points[min] = temp;

   // Sort n-1 points with respect to the first point.
   // A point p1 comes before p2 in sorted output if p2
   // has larger polar angle (in counterclockwise
   // direction) than p1
   p0 = points[0];
   points.sort(compare);

   // Now stack has the output points, print contents
   // of stack
   for (let i=0; i<n; i++)
       console.log("(" + points[i][0] + "," + points[i][1] + "), ");
}

// Driver program to test above functions
let points = [[0, 3], [1, 1], [2, 2], [4, 4], [0, 0], [1, 2], [3, 1], [3, 3]];
let n = points.length;

printClosedPath(points, n);

// The code is contributed by Nidhi goel.

Output: 

(0, 0), (3, 1), (1, 1), (2, 2), (3, 3),
(4, 4), (1, 2), (0, 3), 

Time complexity of above solution is O(n Log n) if we use a O(nLogn) sorting algorithm for sorting points.
Auxiliary Space: O(1), since no extra space has been taken.

Source: 
http://www.dcs.gla.ac.uk/~pat/52233/slides/Geometry1x1.pdf
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above