Find the Missing Point of Parallelogram

Given three coordinate points A, B and C, find the missing point D such that ABCD can be a parallelogram.
Examples :

Input : A = (1, 0)
        B = (1, 1)
        C = (0, 1)
Output : 0, 0
Explanation:
The three input points form a unit
square with the point (0, 0)

Input : A = (5, 0)
        B = (1, 1)
        C = (2, 5)
Output : 6, 4

As shown in below diagram, there can be multiple possible outputs, we need to print any one of them. 

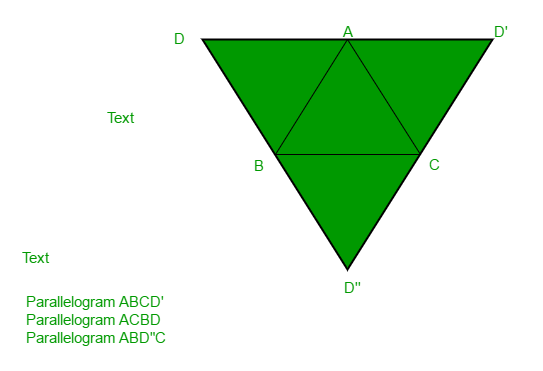
A quadrilateral is said to be a parallelogram if its opposite sides are parallel and equal in length. 

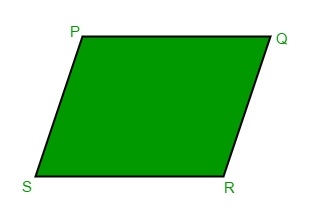
As we’re given three points of the parallelogram, we can find the slope of the missing sides as well as their lengths. 
The algorithm can be explained as follows
Let R be the missing point. Now from definition, we have 

• Length of PR = Length of QS = L1 (Opposite sides are equal)
• Slope of PR = Slope of QS = M1 (Opposite sides are parallel)
• Length of PQ = Length of RS = L2 (Opposite sides are equal)
• Slope of PQ= Slope of RS = M2 (Opposite sides are parallel)

Thus we can find the points at a distance L1 from P having slope M1 as mentioned in below article : 
Find points at a given distance on a line of given slope.
Now one of the points will satisfy the above conditions which can easily be checked (using either condition 3 or 4)

Below is the implementation of the above approach: 

C++

// C++ program to find missing point of a
// parallelogram
#include <bits/stdc++.h>
using namespace std;

// struct to represent a co-ordinate point
struct Point {
    float x, y;
    Point()
    {
        x = y = 0;
    }
    Point(float a, float b)
    {
        x = a, y = b;
    }
};

// given a source point, slope(m) of line
// passing through it this function calculates
// and return two points at a distance l away
// from the source
pair<Point, Point> findPoints(Point source,
                              float m, float l)
{
    Point a, b;

    // slope is 0
    if (m == 0) {
        a.x = source.x + l;
        a.y = source.y;

        b.x = source.x - l;
        b.y = source.y;
    }

    // slope if infinity
    else if (m == std::numeric_limits<float>::max()) {
        a.x = source.x;
        a.y = source.y + l;

        b.x = source.x;
        b.y = source.y - l;
    }

    // normal case
    else {
        float dx = (l / sqrt(1 + (m * m)));
        float dy = m * dx;
        a.x = source.x + dx, a.y = source.y + dy;
        b.x = source.x - dx, b.y = source.y - dy;
    }

    return pair<Point, Point>(a, b);
}

// given two points, this function calculates
// the slope of the line/ passing through the
// points
float findSlope(Point p, Point q)
{
    if (p.y == q.y)
        return 0;
    if (p.x == q.x)
        return std::numeric_limits<float>::max();
    return (q.y - p.y) / (q.x - p.x);
}

// calculates the distance between two points
float findDistance(Point p, Point q)
{
    return sqrt(pow((q.x - p.x), 2) + pow((q.y - p.y), 2));
}

// given three points, it prints a point such
// that a parallelogram is formed
void findMissingPoint(Point a, Point b, Point c)
{
    // calculate points originating from a
    pair<Point, Point> d = findPoints(a, findSlope(b, c),
                                      findDistance(b, c));

    // now check which of the two points satisfy
    // the conditions
    if (findDistance(d.first, c) == findDistance(a, b))
        cout << d.first.x << ", " << d.first.y << endl;
    else
        cout << d.second.x << ", " << d.second.y << endl;
}

// Driver code
int main()
{
    findMissingPoint(Point(1, 0), Point(1, 1), Point(0, 1));
    findMissingPoint(Point(5, 0), Point(1, 1), Point(2, 5));
    return 0;
}

Java

// Java program to find missing point of a
// parallelogram
import java.util.*;

// struct to represent a co-ordinate point
class Point {
  public double x, y;
  public Point()
  {
    x = 0;
    y = 0;
  }

  public Point(double a, double b)
  {
    x = a;
    y = b;
  }
};

class GFG {
  // given a source point, slope(m) of line
  // passing through it this function calculates
  // and return two points at a distance l away
  // from the source
  static Point[] findPoints(Point source, double m,
                            double l)
  {
    Point a = new Point();
    Point b = new Point();

    // slope is 0
    if (m == 0) {
      a.x = source.x + l;
      a.y = source.y;

      b.x = source.x - l;
      b.y = source.y;
    }

    // slope if infinity
    else if (m == Double.MAX_VALUE) {
      a.x = source.x;
      a.y = source.y + l;

      b.x = source.x;
      b.y = source.y - l;
    }

    // normal case
    else {
      double dx = (l / Math.sqrt(1 + (m * m)));
      double dy = m * dx;
      a.x = source.x + dx;
      a.y = source.y + dy;
      b.x = source.x - dx;
      b.y = source.y - dy;
    }

    Point[] res = { a, b };
    return res;
  }

  // given two points, this function calculates
  // the slope of the line/ passing through the
  // points
  static double findSlope(Point p, Point q)
  {
    if (p.y == q.y)
      return 0;
    if (p.x == q.x)
      return Double.MAX_VALUE;
    return (q.y - p.y) / (q.x - p.x);
  }

  // calculates the distance between two points
  static double findDistance(Point p, Point q)
  {
    return Math.sqrt(Math.pow((q.x - p.x), 2)
                     + Math.pow((q.y - p.y), 2));
  }

  // given three points, it prints a point such
  // that a parallelogram is formed
  static void findMissingPoint(Point a, Point b, Point c)
  {
    // calculate points originating from a
    Point[] d = findPoints(a, findSlope(b, c),
                           findDistance(b, c));

    // now check which of the two points satisfy
    // the conditions
    if (findDistance(d[0], c) == findDistance(a, b))
      System.out.println(d[0].x + ", " + d[0].y);
    else
      System.out.println(d[1].x + ", " + d[1].y);
  }

  // Driver code
  public static void main(String[] args)
  {
    findMissingPoint(new Point(1, 0), new Point(1, 1),
                     new Point(0, 1));
    findMissingPoint(new Point(5, 0), new Point(1, 1),
                     new Point(2, 5));
  }
}

// This code is contributed by phasing17

Python3

# Python program to find missing point of a
# parallelogram

import math as Math
FLOAT_MAX = 3.40282e+38

# given a source point, slope(m) of line
# passing through it this function calculates
# and return two points at a distance l away
# from the source


def findPoints(source, m, l):
    a = [0] * (2)
    b = [0] * (2)

    # slope is 0
    if (m == 0):
        a[0] = source[0] + l
        a[1] = source[1]

        b[0] = source[0] - l
        b[1] = source[1]
    # slope if infinity
    elif (m == FLOAT_MAX):
        a[0] = source[0]
        a[1] = source[1] + l

        b[0] = source[0]
        b[1] = source[1] - l
    # normal case
    else:
        dx = (l / ((1 + (m * m)) ** 0.5))
        dy = m * dx
        a[0] = source[0] + dx
        a[1] = source[1] + dy
        b[0] = source[0] - dx
        b[1] = source[1] - dy

    return [a, b]


# given two points, this function calculates
# the slope of the line/ passing through the
# points
def findSlope(p, q):
    if (p[1] == q[1]):
        return 0
    if (p[0] == q[0]):
        return FLOAT_MAX
    return (q[1] - p[1]) / (q[0] - p[0])


# calculates the distance between two points
def findDistance(p, q):
    return Math.sqrt(Math.pow((q[0] - p[0]), 2) + Math.pow((q[1] - p[1]), 2))


# given three points, it prints a point such
# that a parallelogram is formed
def findMissingPoint(a, b, c):
    # calculate points originating from a
    d = findPoints(a, findSlope(b, c), findDistance(b, c))

    # now check which of the two points satisfy
    # the conditions
    if (findDistance(d[0], c) == findDistance(a, b)):
        print(f"{(int)(d[0][0])}, {(int)(d[0][1])}")

    else:
        print(f"{(int)(d[1][0])}, {(int)(d[1][1])}")


# Driver code
Point1 = [1, 0]
Point2 = [1, 1]
Point3 = [0, 1]
findMissingPoint(Point1, Point2, Point3)

Point1 = [5, 0]
Point2 = [1, 1]
Point3 = [2, 5]
findMissingPoint(Point1, Point2, Point3)

# The code is contributed by Saurabh Jaiswal

C#

// C# program to find missing point of a
// parallelogram
using System;
using System.Collections.Generic;

// struct to represent a co-ordinate point
class Point {
  public double x, y;
  public Point()
  {
    x = 0;
    y = 0;
  }

  public Point(double a, double b)
  {
    x = a;
    y = b;
  }
};

class GFG
{

  // given a source point, slope(m) of line
  // passing through it this function calculates
  // and return two points at a distance l away
  // from the source
  static Point[] findPoints(Point source, double m,
                            double l)
  {
    Point a = new Point();
    Point b = new Point();

    // slope is 0
    if (m == 0) {
      a.x = source.x + l;
      a.y = source.y;

      b.x = source.x - l;
      b.y = source.y;
    }

    // slope if infinity
    else if (m == Double.MaxValue) {
      a.x = source.x;
      a.y = source.y + l;

      b.x = source.x;
      b.y = source.y - l;
    }

    // normal case
    else {
      double dx = (l / Math.Sqrt(1 + (m * m)));
      double dy = m * dx;
      a.x = source.x + dx;
      a.y = source.y + dy;
      b.x = source.x - dx;
      b.y = source.y - dy;
    }

    Point[] res = { a, b };
    return res;
  }

  // given two points, this function calculates
  // the slope of the line/ passing through the
  // points
  static double findSlope(Point p, Point q)
  {
    if (p.y == q.y)
      return 0;
    if (p.x == q.x)
      return Double.MaxValue;
    return (q.y - p.y) / (q.x - p.x);
  }

  // calculates the distance between two points
  static double findDistance(Point p, Point q)
  {
    return Math.Sqrt(Math.Pow((q.x - p.x), 2)
                     + Math.Pow((q.y - p.y), 2));
  }

  // given three points, it prints a point such
  // that a parallelogram is formed
  static void findMissingPoint(Point a, Point b, Point c)
  {
    // calculate points originating from a
    Point[] d = findPoints(a, findSlope(b, c),
                           findDistance(b, c));

    // now check which of the two points satisfy
    // the conditions
    if (findDistance(d[0], c) == findDistance(a, b))
      Console.WriteLine(d[0].x + ", " + d[0].y);
    else
      Console.WriteLine(d[1].x + ", " + d[1].y);
  }

  // Driver code
  public static void Main(string[] args)
  {
    findMissingPoint(new Point(1, 0), new Point(1, 1),
                     new Point(0, 1));
    findMissingPoint(new Point(5, 0), new Point(1, 1),
                     new Point(2, 5));
  }
}

// This code is contributed by phasing17

Javascript

// JavaScript program to find missing point of a
// parallelogram

const FLOAT_MAX = 3.40282e+38;

// given a source point, slope(m) of line
// passing through it this function calculates
// and return two points at a distance l away
// from the source
function findPoints(source, m, l)
{
    let a = new Array(2);
    let b = new Array(2);

    // slope is 0
    if (m == 0) {
        a[0] = source[0] + l;
        a[1] = source[1];

        b[0] = source[0] - l;
        b[1] = source[1];
    }
    // slope if infinity
    else if (m == FLOAT_MAX) {
        a[0] = source[0];
        a[1] = source[1] + l;

        b[0] = source[0];
        b[1] = source[1] - l;
    }
    // normal case
    else {
        let dx = (l / Math.sqrt(1 + (m * m)));
        let dy = m * dx;
        a[0] = source[0] + dx, a[1] = source[1] + dy;
        b[0] = source[0] - dx, b[1] = source[1] - dy;
    }

    return [a, b];
}

// given two points, this function calculates
// the slope of the line/ passing through the
// points
function findSlope(p, q)
{
    if (p[1] == q[1]){
        return 0;
    }
    if (p[0] == q[0]){
        return FLOAT_MAX;
    }
    return (q[1] - p[1]) / (q[0] - p[0]);
}

// calculates the distance between two points
function findDistance(p, q)
{
    return Math.sqrt(Math.pow((q[0] - p[0]), 2) + Math.pow((q[1] - p[1]), 2));
}

// given three points, it prints a point such
// that a parallelogram is formed
function findMissingPoint(a, b, c)
{
    // calculate points originating from a
    let d = findPoints(a, findSlope(b, c), findDistance(b, c));

    // now check which of the two points satisfy
    // the conditions
    if (findDistance(d[0], c) === findDistance(a, b)){
        console.log(d[0][0], ",", d[0][1]);
    }
    else{
        console.log(d[1][0], ",", d[1][1]);
    }
}

// Driver code
{
    let Point1 = [1, 0];
    let Point2 = [1, 1];
    let Point3 = [0, 1];
    findMissingPoint(Point1, Point2, Point3);

    Point1 = [5, 0];
    Point2 = [1, 1];
    Point3 = [2, 5];
    findMissingPoint(Point1, Point2, Point3);
}

// The code is contributed by Gautam goel (gautamgoel962)

Output :

0, 0
6, 4

Time Complexity: O(log(log n)) since using inbuilt sqrt and log functions 
Auxiliary Space: O(1)

Alternative Approach:

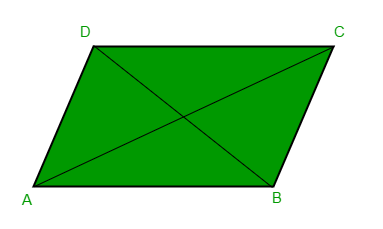
Since the opposite sides are equal, AD = BC and AB = CD, we can calculate the co-ordinates of the missing point (D) as: 

AD = BC
(Dx - Ax, Dy - Ay) = (Cx - Bx, Cy - By)
Dx = Ax + Cx - Bx 
Dy = Ay + Cy - By

References: https://math.stackexchange.com/questions/887095/find-the-4th-vertex-of-the-parallelogram
Below is the implementation of above approach:

C++

// C++ program to find missing point
// of a parallelogram
#include <bits/stdc++.h>
using namespace std;

// main method
int main()
{
   int ax = 5, ay = 0; //coordinates of A
   int bx = 1, by = 1; //coordinates of B
   int cx = 2, cy = 5; //coordinates of C
    cout << ax + cx - bx << ", "
         << ay + cy - by;
    return 0;
}

Java

// Java program to
// find missing point
// of a parallelogram
import java.io.*;

class GFG
{
public static void main (String[] args)
{

    int ax = 5, ay = 0; //coordinates of A
    int bx = 1, by = 1; //coordinates of B
    int cx = 2, cy = 5; //coordinates of C
    System.out.println(ax + (cx - bx) + ", " +
                       ay + (cy - by));
}
}

// This code is contributed by m_kit

Python 3

# Python 3 program to find missing point
# of a parallelogram

# Main method
if __name__ == "__main__":

    # coordinates of A

    ax, ay = 5, 0

    # coordinates of B

    bx ,by = 1, 1

    # coordinates of C

    cx ,cy = 2, 5

    print(ax + cx - bx , ",", ay + cy - by)

# This code is contributed by Smitha

C#

// C# program to
// find missing point
// of a parallelogram
using System;

class GFG
{
    static public void Main ()
    {
        int ax = 5, ay = 0; //coordinates of A
        int bx = 1, by = 1; //coordinates of B
        int cx = 2, cy = 5; //coordinates of C
        Console.WriteLine(ax + (cx - bx) + ", " +
                             ay + (cy - by));
    }
}

// This code is contributed by ajit

PHP

<?php
// PHP program to find missing
// point of a parallelogram

// Driver Code
$ax = 5;
$ay = 0; //coordinates of A
$bx = 1;
$by = 1; //coordinates of B
$cx = 2;
$cy = 5; //coordinates of C
echo $ax + $cx - $bx , ", ",
     $ay + $cy - $by;

// This code is contributed by aj_36
?>

Javascript

<script>
    // Javascript program to find missing point of a parallelogram

    let ax = 5, ay = 0; //coordinates of A
    let bx = 1, by = 1; //coordinates of B
    let cx = 2, cy = 5; //coordinates of C
    document.write((ax + (cx - bx)) + ", " + (ay + (cy - by)));

</script>

Output:

6, 4

Time Complexity: O(1) 
Auxiliary Space: O(1)

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.