Equation of ellipse from its focus, directrix, and eccentricity
Last Updated :
23 Jul, 2022
Given focus(x, y), directrix(ax + by + c) and eccentricity e of an ellipse, the task is to find the equation of ellipse using its focus, directrix, and eccentricity.
Examples:
Input: x1 = 1, y1 = 1, a = 1, b = -1, c = 3, e = 0.5
Output: 1.75 x^2 + 1.75 y^2 + -5.50 x + -2.50 y + 0.50 xy + 1.75 = 0
Input: x1 = -1, y1 = 1, a = 1, b = -1, c = 3, e = 0.5
Output: 1.75 x^2 + 1.75 y^2 + 2.50 x + -2.50 y + 0.50 xy + 1.75 = 0
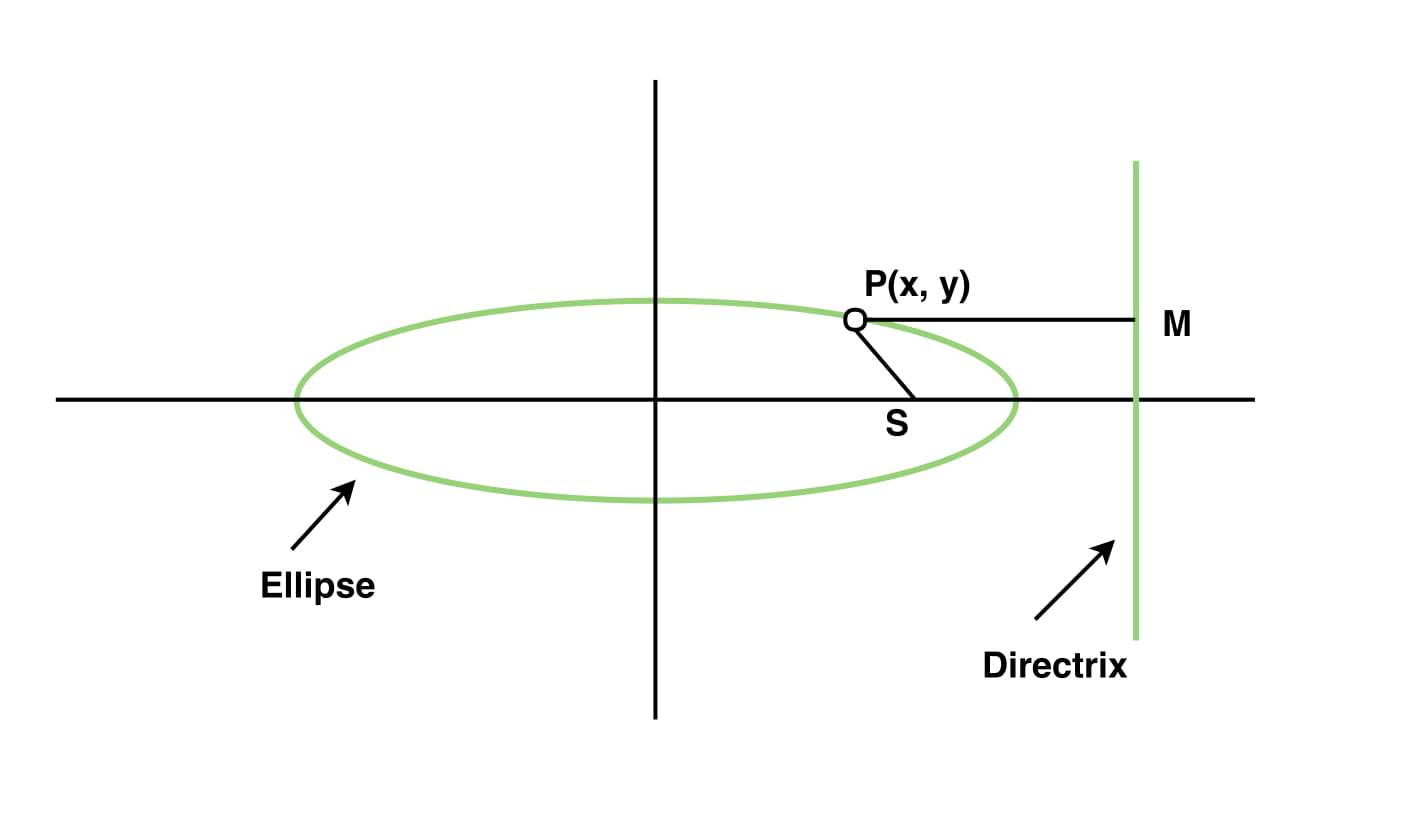
Let P(x, y) be any point on the ellipse whose focus S(x1, y1), directrix is the straight line ax + by + c = 0 and eccentricity is e.
Draw PM perpendicular from P on the directrix. Then by definition of ellipse distance SP = e * PM => SP^2 = (e * PM)^2
(x – x1)^2 + (y – y1)^2 = e * ( ( a*x + b*y + c ) / (sqrt( a*a + b*b )) ) ^ 2
let ( a*a + b*b ) = t
x^2 + x1^2 – 2*x1*x + y^2 + y1^2 – 2*y1*y = e * ( ( a*x + b*y + c ) ^ 2 )/ t
on cross multiplying above we get
t*x^2 + t*x1^2 – 2*t*x1*x + t*y^2 + t*y1^2 – 2*t*y1*y = e * ( ( a*x + b*y + c ) ^ 2 )
t*x^2 + t*x1^2 – 2*t*x1*x + t*y^2 + t*y1^2 – 2*t*y1*y = e*a^2*x^2 + e*b^2*y^2 + 2*e*a*x*b*y + e*c^2 + 2*e*c*(a*x + b*y)
t*x^2 + t*x1^2 – 2*t*x1*x + t*y^2 + t*y1^2 – 2*t*y1*y = e*a^2*x^2 + e*b^2*y^2 + 2*e*a*x*b*y + e*c^2 + 2*e*c*a*x + 2*e*c*b*y
t*x^2 – e*a^2*x^2 + t*y^2 – e*b^2*y^2 – 2*t*x1*x – 2*e*c*a*x – 2*t*y1*y – 2*e*c*b*y – 2*e*a*x*b*y – e*c^2 + t*x1^2 + t*y1^2 =0
This can be compared with a general form that is:
a*x^2 + 2*h*x*y + b*y^2 + 2*g*x + 2*f*y + c = 0
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
#include <iomanip>
#include <iostream>
#include <math.h>
using namespace std;
void equation_ellipse(float x1, float y1,
float a, float b,
float c, float e)
{
float t = a * a + b * b;
float a1 = t - e * (a * a);
float b1 = t - e * (b * b);
float c1 = (-2 * t * x1) - (2 * e * c * a);
float d1 = (-2 * t * y1) - (2 * e * c * b);
float e1 = -2 * e * a * b;
float f1 = (-e * c * c) + (t * x1 * x1) + (t * y1 * y1);
cout << fixed;
cout << setprecision(2);
cout << "Equation of ellipse is \n"
<< a1
<< " x^2 + " << b1 << " y^2 + "
<< c1 << " x + " << d1 << " y + "
<< e1 << " xy + " << f1 << " = 0";
}
int main()
{
float x1 = 1, y1 = 1, a = 1, b = -1, c = 3, e = 0.5 * 0.5;
equation_ellipse(x1, y1, a, b, c, e);
return 0;
}
|
Java
import java.util.*;
class solution
{
static void equation_ellipse(float x1, float y1,
float a, float b,
float c, float e)
{
float t = a * a + b * b;
float a1 = t - e * (a * a);
float b1 = t - e * (b * b);
float c1 = (-2 * t * x1) - (2 * e * c * a);
float d1 = (-2 * t * y1) - (2 * e * c * b);
float e1 = -2 * e * a * b;
float f1 = (-e * c * c) + (t * x1 * x1) + (t * y1 * y1);
System.out.println("Equation of ellipse is ");
System.out.print(a1+" x^2 + "+ b1 + " y^2 + "+ c1 + " x + "
+ d1 + " y + " + e1 + " xy + " + f1 + " = 0");
}
public static void main(String arr[])
{
float x1 = 1, y1 = 1, a = 1, b = -1, c = 3, e = (float)0.5 * (float)0.5;
equation_ellipse(x1, y1, a, b, c, e);
}
}
|
Python3
def equation_ellipse(x1, y1, a, b, c, e) :
t = a * a + b * b
a1 = t - e * (a * a)
b1 = t - e * (b * b)
c1 = (-2 * t * x1) - (2 * e * c * a)
d1 = (-2 * t * y1) - (2 * e * c * b)
e1 = -2 * e * a * b
f1 = (-e * c * c) + (t * x1 * x1) + (t * y1 * y1)
print("Equation of ellipse is",a1,"x^2 +", b1 ,"y^2 +",
c1, "x +" ,d1 ,"y +", e1 ,"xy +" , f1 ,"= 0")
if __name__ == "__main__" :
x1, y1, a, b, c, e = 1, 1, 1, -1, 3, 0.5 * 0.5
equation_ellipse(x1, y1, a, b, c, e)
|
C#
class solution
{
static void equation_ellipse(float x1, float y1,
float a, float b,
float c, float e)
{
float t = a * a + b * b;
float a1 = t - e * (a * a);
float b1 = t - e * (b * b);
float c1 = (-2 * t * x1) - (2 * e * c * a);
float d1 = (-2 * t * y1) - (2 * e * c * b);
float e1 = -2 * e * a * b;
float f1 = (-e * c * c) + (t * x1 * x1) + (t * y1 * y1);
System.Console.WriteLine("Equation of ellipse is ");
System.Console.WriteLine(a1+" x^2 + "+ b1 + " y^2 + "+ c1 + " x + "
+ d1 + " y + " + e1 + " xy + " + f1 + " = 0");
}
public static void Main()
{
float x1 = 1, y1 = 1, a = 1, b = -1, c = 3, e = (float)0.5 * (float)0.5;
equation_ellipse(x1, y1, a, b, c, e);
}
}
|
PHP
<?php
function equation_ellipse($x1, $y1, $a,
$b, $c, $e)
{
$t = ($a * $a) + ($b * $b);
$a1 = $t - $e * ($a * $a);
$b1 = $t - $e * ($b * $b);
$c1 = (-2 * $t * $x1) -
(2 * $e * $c * $a);
$d1 = (-2 * $t * $y1) -
(2 * $e * $c * $b);
$e1 = -2 * $e * $a * $b;
$f1 = (-$e * $c * $c) +
($t * $x1 * $x1) + ($t * $y1 * $y1);
$fixed;
echo "Equation of ellipse is \n" ,
$a1, " x^2 + ", $b1 , " y^2 + ",
$c1 , " x + " , $d1 , " y + ",
$e1 , " xy + " , $f1 , " = 0";
}
$x1 = 1; $y1 = 1;
$a = 1;
$b = -1;
$c = 3;
$e = 0.5 * 0.5;
equation_ellipse($x1, $y1, $a,
$b, $c, $e);
?>
|
Javascript
<script>
function equation_ellipse(x1, y1, a, b, c, e)
{
var t = a * a + b * b;
var a1 = t - e * (a * a);
var b1 = t - e * (b * b);
var c1 = (-2 * t * x1) - (2 * e * c * a);
var d1 = (-2 * t * y1) - (2 * e * c * b);
var e1 = -2 * e * a * b;
var f1 = (-e * c * c) + (t * x1 * x1) + (t * y1 * y1);
document.write("Equation of ellipse is " + "<br>");
document.write(a1+" x^2 + "+ b1 + " y^2 + "+ c1 + " x + "
+ d1 + " y + " + e1 + " xy + " + f1 + " = 0");
}
var x1 = 1, y1 = 1, a = 1, b = -1, c = 3, e = 0.5 * 0.5;
equation_ellipse(x1, y1, a, b, c, e);
</script>
|
Output:
Equation of ellipse is
1.75 x^2 + 1.75 y^2 + -5.50 x + -2.50 y + 0.50 xy + 1.75 = 0
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...