Number of parallelograms when n horizontal parallel lines intersect m vertical parallel lines
Last Updated :
12 Nov, 2023
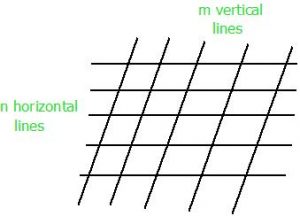
Given two positive integers n and m. The task is to count number of parallelogram that can be formed of any size when n horizontal parallel lines intersect with m vertical parallel lines.
Examples:
Input : n = 3, m = 2
Output : 3
2 parallelograms of size 1x1 and 1 parallelogram
of size 2x1.
Input : n = 5, m = 5
Output : 100
The idea is to use Combination, which state, number of ways to choose k items from given n items is given by nCr.
To form a parallelogram, we need two horizontal parallel lines and two vertical parallel lines. So, number of ways to choose two horizontal parallel lines are nC2 and number of ways to choose two vertical parallel lines are mC2. So, total number of possible parallelogram will be nC2 x mC2.
Below is C++ implementation of this approach:
C++
#include<bits/stdc++.h>
#define MAX 10
using namespace std;
int binomialCoeff(int C[][MAX], int n, int k)
{
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i-1][j-1] + C[i-1][j];
}
}
}
int countParallelogram(int n, int m)
{
int C[MAX][MAX] = { 0 };
binomialCoeff(C, max(n, m), 2);
return C[n][2] * C[m][2];
}
int main()
{
int n = 5, m = 5;
cout << countParallelogram(n, m) << endl;
return 0;
}
|
Java
class GFG
{
static final int MAX = 10;
static void binomialCoeff(int C[][], int n, int k)
{
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
static int countParallelogram(int n, int m)
{
int C[][]=new int[MAX][MAX];
binomialCoeff(C, Math.max(n, m), 2);
return C[n][2] * C[m][2];
}
public static void main(String arg[])
{
int n = 5, m = 5;
System.out.println(countParallelogram(n, m));
}
}
|
Python3
MAX = 10;
def binomialCoeff(C, n, k):
for i in range(n + 1):
for j in range(0, min(i, k) + 1):
if (j == 0 or j == i):
C[i][j] = 1;
else:
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
def countParallelogram(n, m):
C = [[0 for i in range(MAX)] for j in range(MAX)]
binomialCoeff(C, max(n, m), 2);
return C[n][2] * C[m][2];
if __name__ == '__main__':
n = 5;
m = 5;
print(countParallelogram(n, m));
|
C#
using System;
class GFG
{
static int MAX = 10;
static void binomialCoeff(int [,]C, int n, int k)
{
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= Math.Min(i, k); j++)
{
if (j == 0 || j == i)
C[i, j] = 1;
else
C[i, j] = C[i - 1, j - 1] + C[i - 1, j];
}
}
}
static int countParallelogram(int n, int m)
{
int [,]C = new int[MAX, MAX];
binomialCoeff(C, Math.Max(n, m), 2);
return C[n, 2] * C[m, 2];
}
public static void Main()
{
int n = 5, m = 5;
Console.WriteLine(countParallelogram(n, m));
}
}
|
Javascript
<script>
var MAX = 10;
function binomialCoeff(C, n, k)
{
for (var i = 0; i <= n; i++)
{
for (var j = 0; j <= Math.min(i, k); j++)
{
if (j == 0 || j == i)
C[i][j] = 1;
else
C[i][j] = C[i-1][j-1] + C[i-1][j];
}
}
}
function countParallelogram(n, m)
{
var C = Array.from(Array(MAX), () => Array(MAX).fill(0));
binomialCoeff(C, Math.max(n, m), 2);
return C[n][2] * C[m][2];
}
var n = 5, m = 5;
document.write( countParallelogram(n, m));
</script>
|
Time Complexity: O(n2)
Auxiliary Space: O(n2)
Approach: Using Basic Maths
The same Question can be Solved By just using the basic maths
as we know nC2 = n*(n-1)/2 and same for mC2 so just using basic maths we can solve the question in O(1)
Below is the implementation of the above approach:
C++
#include <iostream>
class GFG {
public:
static int findtheParallelogram(int n, int m)
{
int result
= ((n * (n - 1)) / 2) * ((m * (m - 1)) / 2);
return result;
}
};
int main()
{
int n = 5;
int m = 5;
std::cout << GFG::findtheParallelogram(n, m)
<< std::endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
public static int findtheParallelogram(int n, int m) {
int result = ((n * (n - 1)) / 2) * ((m * (m - 1)) / 2);
return result;
}
public static void main(String[] vars){
int n = 5;
int m =5;
System.out.println(findtheParallelogram(n,m));
}
}
|
Python3
def find_the_parallelogram(n, m):
result = ((n * (n - 1)) // 2) * ((m * (m - 1)) // 2)
return result
if __name__ == "__main__":
n = 5
m = 5
print(find_the_parallelogram(n, m))
|
C#
using System;
class GFG {
public static int FindTheParallelogram(int n, int m)
{
int result
= ((n * (n - 1)) / 2) * ((m * (m - 1)) / 2);
return result;
}
}
class Program {
static void Main(string[] args)
{
int n = 5;
int m = 5;
Console.WriteLine("Number of Parallelograms: "
+ GFG.FindTheParallelogram(n, m));
}
}
|
Javascript
class GFG {
static findtheParallelogram(n, m) {
const result = ((n * (n - 1)) / 2) * ((m * (m - 1)) / 2);
return result;
}
}
const n = 5;
const m = 5;
console.log(GFG.findtheParallelogram(n, m));
|
Time Complexity :O(1)
Space Complexity : O(1)
This article is contributed by Aarti_Rathi and Dhruv Khoradiya.
Share your thoughts in the comments
Please Login to comment...