Python Program for Finding the vertex, focus and directrix of a parabola
A set of points on a plain surface that forms a curve such that any point on that curve is equidistant from the focus is a parabola.
Vertex of a parabola is the coordinate from which it takes the sharpest turn whereas a is the straight line used to generate the curve.
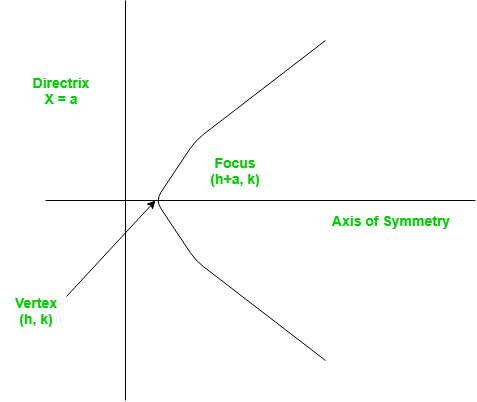
The standard form of a parabola equation is 
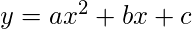
. Given the values of a, b and c; our task is to find the coordinates of vertex, focus and the equation of the directrix.
Example –
Input : 5 3 2
Output : Vertex:(-0.3, 1.55)
Focus: (-0.3, 1.6)
Directrix: y=-198
Consult the formula below for explanation.
Recommended: Please try your approach on {IDE} first, before moving on to the solution.
# Python program to calculate Vertex, Focus and Directrix def parabola(a, b, c): print ("Vertex: (" , (-b / (2 * a)) , ", " ,(((4 * a * c) - (b * b)) / (4 * a)) , ")" ) print ("Focus: (" , (-b / (2 * a)) , ", " , (((4 * a * c) - (b * b) + 1) / (4 * a)) , ")" ) print ("Directrix: y=" , (int)(c - ((b * b) + 1) * 4 * a )) # main()a = 5b = 3c = 2 parabola(a, b, c) # Contributed by _omg |
Output :
Vertex:(-0.3, 1.55) Focus: (-0.3, 1.6) Directrix: y=-198
Please refer complete article on Finding the vertex, focus and directrix of a parabola for more details!
