Check if a line touches or intersects a circle

Given coordinate of the center and radius > 1 of a circle and the equation of a line. The task is to check if the given line collides with the circle or not. There are three possibilities : 

1. Line intersects the circle.
2. Line touches the circle.
3. Line is outside the circle
   

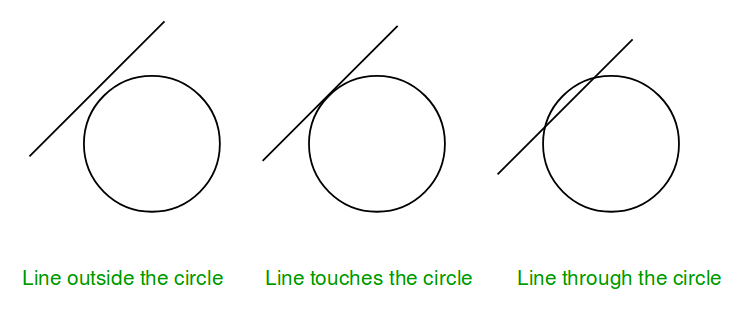
Note: General equation of a line is a*x + b*y + c = 0, so only constant a, b, c are given in the input.

Examples :

Input : radius = 5, center = (0, 0), 
        a = 1, b = -1, c = 0.
Output : Intersect
Input :  radius = 5, center = (0, 0), 
         a = 5, b = 0, c = 0.
Output : Intersect
Input : radius = 5, center = (0, 0),
         a = 1, b = 1, c = -16.
Output : Outside

The idea is to compare the perpendicular distance between center of circle and line with the radius of the circle.
Algorithm: 
1. Find the perpendicular (say p) between center of circle and given line. 
2. Compare this distance p with radius r. 
……a) If p > r, then line lie outside the circle. 
……b) If p = r, then line touches the circle. 
……c) If p < r, then line intersect the circle.
How to find the perpendicular distance?
Distance of a line from a point can be computed using below formula:

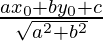
C++

// CPP program to check if a line touches or
// intersects or outside a circle.
#include <bits/stdc++.h>
using namespace std;

void checkCollision(int a, int b, int c,
                  int x, int y, int radius)
{
    // Finding the distance of line from center.
    int dist = (abs(a * x + b * y + c)) /
                     sqrt(a * a + b * b);

    // Checking if the distance is less than,
    // greater than or equal to radius.
    if (radius == dist)
        cout << "Touch" << endl;
    else if (radius > dist)
        cout << "Intersect" << endl;
    else
        cout << "Outside" << endl;
}

// Driven Program
int main()
{
    int radius = 5;
    int x = 0, y = 0;
    int a = 3, b = 4, c = 25;
    checkCollision(a, b, c, x, y, radius);
    return 0;
}

Java

// Java program to check if a line touches or
// intersects or outside a circle.

import java.io.*;

class GFG {

    static void checkCollision(int a, int b, int c,
                               int x, int y, int radius)
    {
        // Finding the distance of line from center.
        double dist = (Math.abs(a * x + b * y + c)) /
                        Math.sqrt(a * a + b * b);

        // Checking if the distance is less than,
        // greater than or equal to radius.
        if (radius == dist)
            System.out.println ( "Touch" );
        else if (radius > dist)
            System.out.println( "Intersect") ;
        else
            System.out.println( "Outside") ;
    }

    // Driven Program
    public static void main (String[] args)
    {
        int radius = 5;
        int x = 0, y = 0;
        int a = 3, b = 4, c = 25;
        checkCollision(a, b, c, x, y, radius);

    }
}

// This article is contributed by vt_m.

Python3

# python program to check if a line
# touches or  intersects or outside
# a circle.

import math

def checkCollision(a, b, c, x, y, radius):

    # Finding the distance of line
    # from center.
    dist = ((abs(a * x + b * y + c)) /
            math.sqrt(a * a + b * b))

    # Checking if the distance is less
    # than, greater than or equal to radius.
    if (radius == dist):
        print("Touch")
    elif (radius > dist):
        print("Intersect")
    else:
        print("Outside")

# Driven Program
radius = 5
x = 0
y = 0
a = 3
b = 4
c = 25
checkCollision(a, b, c, x, y, radius)

# This code is contributed by Sam007

C#

// C# program to check if a line touches or
// intersects or outside a circle.
using System;

class GFG {

    static void checkCollision(int a, int b, int c,
                            int x, int y, int radius)
    {
        // Finding the distance of line from center.
        double dist = (Math.Abs(a * x + b * y + c)) /
                        Math.Sqrt(a * a + b * b);

        // Checking if the distance is less than,
        // greater than or equal to radius.
        if (radius == dist)
            Console.WriteLine ("Touch");
        else if (radius > dist)
            Console.WriteLine("Intersect");
        else
            Console.WriteLine("Outside");
    }

    // Driven Program
    public static void Main ()
    {
        int radius = 5;
        int x = 0, y = 0;
        int a = 3, b = 4, c = 25;

        checkCollision(a, b, c, x, y, radius);

    }
}

// This article is contributed by vt_m.

Javascript

<script>

// JavaScript program to check if a line touches or
// intersects or outside a circle.

function checkCollision(a, b, c, x, y, radius)
    {

        // Finding the distance of line from center.
        let dist = (Math.abs(a * x + b * y + c)) /
                        Math.sqrt(a * a + b * b);

        // Checking if the distance is less than,
        // greater than or equal to radius.
        if (radius == dist)
            document.write ( "Touch" );
        else if (radius > dist)
            document.write( "Intersect") ;
        else
            document.write( "Outside") ;
    }

// Driver Code
        let radius = 5;
        let x = 0, y = 0;
        let a = 3, b = 4, c = 25;
        checkCollision(a, b, c, x, y, radius);

// This code is contributed by susmitakundugoaldanga.
</script>

PHP

<?php
// PHP program to check if a line
// touches or intersects or outside
// a circle.

function checkCollision($a, $b, $c,
                        $x, $y, $radius)
{
    // Finding the distance
    // of line from center.
    $dist = (abs($a * $x + $b * $y + $c)) /
                   sqrt($a * $a + $b * $b);

    // Checking if the distance is less than,
    // greater than or equal to radius.
    if ($radius == $dist)
        echo "Touch";
    else if ($radius > $dist)
        echo "Intersect";
    else
        echo "Outside" ;
}

// Driver Code
$radius = 5;
$x = 0;
$y = 0;
$a = 3;
$b = 4;
$c = 25;
checkCollision($a, $b, $c, $x, $y, $radius);

// This code is contributed by Sam007
?>

Output

Touch

Time Complexity : O(log(a*a + b*b)) as it is using inbuilt sqrt function
Auxiliary Space : O(1)

This article is contributed by Anuj Chauhan. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.