Class 10 NCERT Solutions- Chapter 6 Triangles – Exercise 6.2
Last Updated :
17 Nov, 2022
Theorem 6.1 :
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Theorem 6.2 :
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
Question 1. In Figure, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).

Solution:
(i) Here, In △ ABC,
DE || BC
So, according to Theorem 6.1
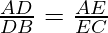
⇒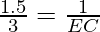
⇒EC =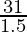
EC = 2 cm
Hence, EC = 2 cm.

(ii) Here, In △ ABC,
So, according to Theorem 6.1 , if DE || BC
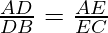
⇒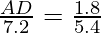
⇒AD =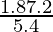
AD = 2.4 cm
Hence, AD = 2.4 cm.
Question 2. E and F are points on the sides PQ and PR respectively of a ∆ PQR. For each of the following cases, state whether EF || QR :

(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
Solution:
According to the Theorem 6.2,
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
So, lets check the ratios
Here, In △ PQR,
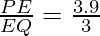 = 1.3 ………………………(i)
= 1.3 ………………………(i)
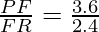 = 1.5 ………………………(ii)
= 1.5 ………………………(ii)
As,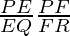
Hence, EF is not parallel to QR.
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
Solution:
According to the Theorem 6.2,
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
So, lets check the ratios
Here, In △ PQR,
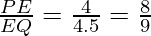 ………………………(i)
………………………(i)
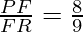 ………………………(ii)
………………………(ii)
As,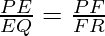
Hence, EF is parallel to QR.
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Solution:
EQ = PQ – PE = 1.28 – 0.18 = 1.1
and, FR = PR – PF = 2.56 – 0.36 = 2.2
According to the Theorem 6.2,
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
So, lets check the ratios
Here, In △ PQR,
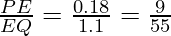 ………………………(i)
………………………(i)
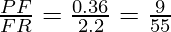 ………………………(ii)
………………………(ii)
As,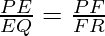
Hence, EF is parallel to QR.
Question 3. In Figure, if LM || CB and LN || CD, prove that
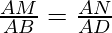

Solution:
Here, In △ ABC,
According to Theorem 6.1, if LM || CB
then,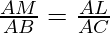 …………………………….(I)
…………………………….(I)
and, In △ ADC,
According to Theorem 6.1, if LN || CD
then,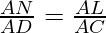 …………………………….(II)
…………………………….(II)
From (I) and (II), we conclude that
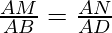
Hence Proved !!
Question 4. In Figure, DE || AC and DF || AE. Prove that
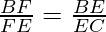

Solution:
Here, In △ ABC,
According to Theorem 6.1, if DE || AC
then,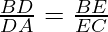 …………………………….(I)
…………………………….(I)
and, In △ ABE,
According to Theorem 6.1, if DF || AE
then,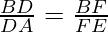 …………………………….(II)
…………………………….(II)
From (I) and (II), we conclude that
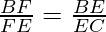
Hence Proved !!
Question 5. In Figure, DE || OQ and DF || OR. Show that EF || QR.

Solution:
Here, In △ POQ,
According to Theorem 6.1, if DE || OQ
then,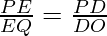 …………………………….(I)
…………………………….(I)
and, In △ POR,
According to Theorem 6.1, if DF || OR
then,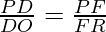 …………………………….(II)
…………………………….(II)
From (I) and (II), we conclude that
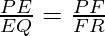 ………………………………(III)
………………………………(III)
According to Theorem 6.2 and eqn. (III)
EF || QR, in △ PQR
Hence Proved !!
Question 6. In Figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Solution:
Here, In △ POQ,
According to Theorem 6.1, if AB || PQ
then,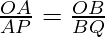 …………………………….(I)
…………………………….(I)
and, In △ POR,
According to Theorem 6.1, if AC || PR
then,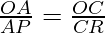 …………………………….(II)
…………………………….(II)
From (I) and (II), we conclude that
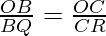 ………………………………(III)
………………………………(III)
According to Theorem 6.2 and eqn. (III)
BC || QR, in △ OQR
Hence Proved !!
Question 7. Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Solution:
Given, in ΔABC, D is the midpoint of AB such that AD=DB.
A line parallel to BC intersects AC at E
So, DE || BC.
We have to prove that E is the mid point of AC.

As, AD=DB
⇒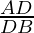 = 1 …………………………. (I)
= 1 …………………………. (I)
Here, In △ ABC,
According to Theorem 6.1, if DE || BC
then,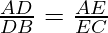 …………………………….(II)
…………………………….(II)
From (I) and (II), we conclude that
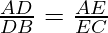 = 1
= 1
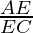 = 1
= 1
AE = EC
E is the midpoint of AC.
Hence proved !!
Question 8. Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Solution:
Given, in ΔABC, D and E are the mid points of AB and AC respectively
AD=BD and AE=EC.
We have to prove that: DE || BC.

As, AD=DB
⇒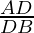 = 1 …………………………. (I)
= 1 …………………………. (I)
and, AE=EC
⇒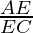 = 1 …………………………. (II)
= 1 …………………………. (II)
From (I) and (II), we conclude that
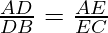 = 1 ……………….(III)
= 1 ……………….(III)
According to Theorem 6.2 and eqn. (III)
DE || BC, in △ ABC
Hence Proved !!
Question 9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that
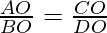
Solution:
From the point O, draw a line EO touching AD at E, in such a way that,
EO || DC || AB

Here, In △ ADB,
According to Theorem 6.1, if AB || EO
then,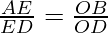 …………………………….(I)
…………………………….(I)
and, In △ ADC,
According to Theorem 6.1, if AC || PR
then,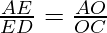 …………………………….(II)
…………………………….(II)
From (I) and (II), we conclude that
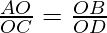
After rearranging, we get
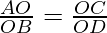
Hence Proved !!
Question 10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that
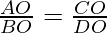 . Show that ABCD is a trapezium.
. Show that ABCD is a trapezium.
Solution:
From the point O, draw a line EO touching AD at E, in such a way that,
EO || DC || AB

Here, In △ ADB,
According to Theorem 6.1, if AB || EO
then,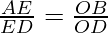 …………………………….(I)
…………………………….(I)
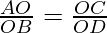 (Given)
(Given)
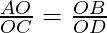 (After rearranging) ………………………………..(II)
(After rearranging) ………………………………..(II)
From (I) and (II), we conclude that
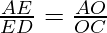 ………………………………..(III)
………………………………..(III)
According to Theorem 6.2 and eqn. (III)
EO || DC and also EO || AB
⇒ AB || DC.
Hence, quadrilateral ABCD is a trapezium with AB || CD.
Share your thoughts in the comments
Please Login to comment...