Class 9 NCERT Solutions- Chapter 7 Triangles – Exercise 7.3

Question 1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Figure). If AD is extended to intersect BC at P, show that

(i) ΔABD ≅ ΔACD

(ii) ΔABP ≅ ΔACP

(iii) AP bisects ∠A as well as ∠D.

(iv) AP is the perpendicular bisector of BC.

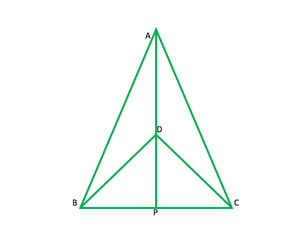
Solution:

Given: ∆ABC and ∆DCB are isosceles ∆on the same base BC.

To show:

• ΔABD ≅ ΔACD
• ΔABP ≅ ΔACP
• AP bisects ∠A as well as ∠D.
• AP is the perpendicular bisector of BC.

i) in ∆ABD and ∆ACB

AB=AC

BD=CD

AD=AD

∆ABD≅∆ACD ————-(S.S.S)

ii) in ∆ABP and ∆ACP

AB=AC

∠ BAP≅∠CAP    [∆ABD≅∆ACD   BY C.P.CT]

AP=AP   ———[common]

∴[∆ABD≅∆ACD         ———–[S.A.S]

iii) [∆ABD≅∆ACD         ———–[S.A.S]

∠BAD=∠CAD

AD, bisects ∠A

AP, bisects ∠A   —————–1

In ∆ BDP and ∆DPB

BD=CD   —————(GIVEN)

DP=PC     ———-[∆AB≅ ∆ACP   C.P.C.T]

DP=DP         ———–[common]

∴∆BDP≅∆CDP    (S.S.S)  

∠BDP=∠CDP  (C.P.C.T)

DP bisects ∠D

AP bisects ∠D  ——————-2

From 1 and 2, AP bisects ∠ A as well as ∠ D

iv) ∠ AP +∠APC =180°        ————[linear pair]

∠APB=∠APC    ————-[∆ABP≅∆ACP       C.P.CT]

∠APB + ∠APC=180°

2 ∠ APB=180°

∠APB=180/2=90°

BP=PC            (FROM ii)

∴AP is ⊥ bisects of BC.

Question 2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that

(i) AD bisects BC                      (ii) AD bisects ∠A.

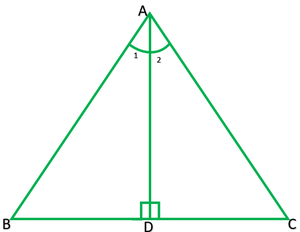
Solution:

Given: AB=AC,  AD altitude

To Show: 

(i) AD bisects BC                      (ii) AD bisects ∠A.

In ∆ADB and ∆ADC

∠ADB=∠ADC   ——– ———–[each 90°]   R

AB=AC               ——————–[given]S

AD=AD             ——–[common]S

∴ ∆ADB ≅∆ADC

BD=DC             ————-[c.p.c.t]

∴AD bisects BC

∠1=∠2               ————-[c.p.c.t]

∴AD bisects ∠A

Question 3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:

(i) ΔABM ≅ ΔPQN

(ii) ΔABC ≅ PQR

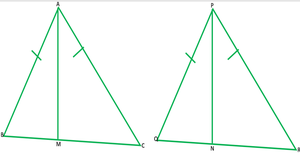
Solution:

Given:  

AB=PQ

BC=QR

AM=PN

AM and PN are medians

To show:(i) ΔABM ≅ ΔPQN           (ii) ΔABC ≅ PQR

Solution: In  ΔABM and ΔPQN  

AB=PQ

AM=PN

because AM and PN are medians BC=QR

therefore   =1/2BC=1/2QR  

∴BM=QN

∴) ΔABM ≅ ΔPQN                    ———[S.S.S]

        ∠B=∠Q             ——–[c.p.c.t]

ii)now in       ΔABC and  ΔPQR    

AB=PQ                ———-[given]

∠B=∠Q             from (i)

BC=QR               —————-[given]

∴ ΔABC ≅ PQR                 [S.A.S]

Question 4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

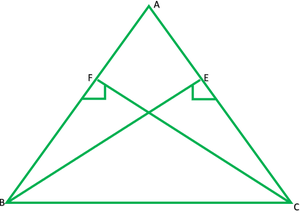
Solution:

Given: altitude BE and CF are equal  

To prove: ΔABC is an isosceles  Δ

In ΔBEC and ΔCEB

∠E=∠F        —————-[each 90°] R

BC=BC       —————–[common]  H

BF=CF       —————-[given]  S

# ΔBEC ≅ ΔCEB     [R.H.S]

∠C=∠B        ————-[C.P.C.T]

 In ΔABC,

∠C=∠B        

 Question 5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.

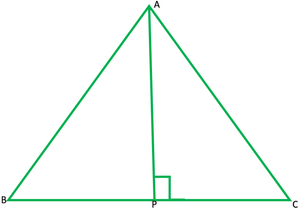
Solution:

Given:

In ∆ABC,

AB=BC

AP ⊥ BC

to show that: ∠B = ∠C.

Solution:  

In ∆APB and ∆APC

∠APB = ∠APC         —————[ each 90°]  R

AB=AC               ——————-[given]      H

AP=AP         ——————–[common]     S

∴∆APB ≅ ∆APC            ———-[R.H.S]

∠B = ∠C  —————[C.P.C.T]