Hash Function
A Hash function is a function that maps any kind of data of arbitrary size to fixed-size values. The values returned by the function are called Hash Values or digests. There are many popular Hash Functions such as DJBX33A, MD5, and SHA-256. This post will discuss the key features, implementation, advantages and drawbacks of the Polynomial Rolling Hash Function.
Note that if two strings are equal, their hash values should also be equal. But the inverse need not be true.
The polynomial rolling hash function
Polynomial rolling hash function is a hash function that uses only multiplications and additions. The following is the function:
![Rendered by QuickLaTeX.com \text{hash(s)} = \text{s}[0] + \text{s}[1]\cdot p + \text{s}[2]\cdot p^2 + \dots + \text{s}[n - 1]\times p^{n - 1}\quad \text{mod}\ m](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-328841da66c5cf68542820f080662a12_l3.png)
or simply,
![Rendered by QuickLaTeX.com \text{hash(s)} = \displaystyle\sum_{i = 0}^{n - 1} s[i]\cdot p^i\quad \text{mod}\ m](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52c85adb02a08daaea4f4c229eeb62d6_l3.png)
Where
- The input to the function is a string
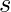 of length
of length 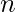 .
. 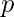 and
and 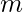 are some positive integers.
are some positive integers.- The choice of
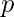 and
and 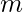 affects the performance and the security of the hash function.
affects the performance and the security of the hash function. - If the string
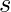 consists of only lower-case letters, then
consists of only lower-case letters, then 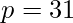 is a good choice.
is a good choice.- Competitive Programmers prefer using a larger value for
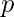 . Examples include
. Examples include 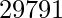 ,
, 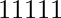 ,
, 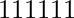 .
.
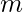 shall necessarily be a large prime since the probability of two keys colliding (producing the same hash) is nearly
shall necessarily be a large prime since the probability of two keys colliding (producing the same hash) is nearly  .
. 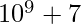 and
and 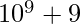 are widely used values for
are widely used values for 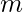 .
.- The output of the function is the hash value of the string
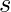 which ranges between
which ranges between 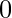 and
and 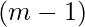 inclusive.
inclusive.
Below is the implementation of the Polynomial Rolling Hash Function
C++
#include <bits/stdc++.h>
using namespace std;
struct Hash {
long long p = 31, m = 1e9 + 7;
long long hash_value;
Hash(const string& s)
{
long long hash_so_far = 0;
long long p_pow = 1;
const long long n = s.length();
for (long long i = 0; i < n; ++i) {
hash_so_far
= (hash_so_far + (s[i] - 'a' + 1) * p_pow)
% m;
p_pow = (p_pow * p) % m;
}
hash_value = hash_so_far;
}
bool operator==(const Hash& other)
{
return (hash_value == other.hash_value);
}
};
int main()
{
const string s = "geeksforgeeks";
Hash h(s);
cout << "Hash of " << s << " is: " << h.hash_value
<< '\n';
return 0;
}
|
C
#include <stdio.h>
#include <string.h>
int get_hash(const char* s, const int n) {
long long p = 31, m = 1e9 + 7;
long long hash = 0;
long long p_pow = 1;
for(int i = 0; i < n; i++) {
hash = (hash + (s[i] - 'a' + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
return hash;
}
int main() {
char s[] = "geeksforgeeks";
int n = strlen(s);
printf("Hash of %s is %d\n", s, get_hash(s, n));
return 0;
}
|
Java
class Hash {
final int p = 31, m = 1000000007;
int hash_value;
Hash(String S)
{
int hash_so_far = 0;
final char[] s = S.toCharArray();
long p_pow = 1;
final int n = s.length;
for (int i = 0; i < n; i++) {
hash_so_far = (int)((hash_so_far
+ (s[i] - 'a' + 1) * p_pow)
% m);
p_pow = (p_pow * p) % m;
}
hash_value = hash_so_far;
}
}
class Main {
public static void main(String[] args)
{
String s = "geeksforgeeks";
Hash h = new Hash(s);
System.out.println("Hash of " + s + " is "
+ h.hash_value);
}
}
|
Python3
class Hash:
def __init__(self, s: str):
self.hash_value = 0
self.p, self.m = 31, 10**9 + 7
self.length = len(s)
hash_so_far = 0
p_pow = 1
for i in range(self.length):
hash_so_far = (hash_so_far + (1 + ord(s[i]) - ord('a')) * p_pow) % self.m
p_pow = (p_pow * self.p) % self.m
self.hash_value = hash_so_far
def __eq__(self, other):
return self.hash_value == other.hash_value
if __name__ == '__main__':
s = "geeksforgeeks"
h = Hash(s)
print("Hash value of {} is {}".format(s, h.hash_value))
|
C#
using System;
public struct Hash
{
public long p;
public long m;
public long hash_value;
public Hash(string s)
{
p = 31;
m = 1000000007;
long hash_so_far = 0;
long p_pow = 1;
long n = s.Length;
for (long i = 0; i < n; ++i)
{
hash_so_far = (hash_so_far + (s[(int)i] - 'a' + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
hash_value = hash_so_far;
}
public static bool operator ==(Hash a, Hash b)
{
return a.hash_value == b.hash_value;
}
public static bool operator !=(Hash a, Hash b)
{
return !(a == b);
}
}
public class MainClass
{
public static void Main()
{
string s = "geeksforgeeks";
Hash h = new Hash(s);
Console.WriteLine($"Hash of {s} is: {h.hash_value}");
}
}
|
Javascript
function get_hash(s) {
const p = 31;
const m = 1e9 + 7;
let hash = 0;
let pPow = 1;
for (let i = 0; i < s.length; i++) {
hash = (hash + (s.charCodeAt(i) - 'a'.charCodeAt(0) + 1) * pPow) % m;
pPow = (pPow * p) % m;
}
return hash;
}
const s = "geeksforgeeks";
console.log(`Hash of ${s} is ${get_hash(s)}`);
|
OutputHash of geeksforgeeks is 609871790
Time Complexity: O(N)
Auxiliary Space: O(1)
Collisions in Polynomial Rolling Hash
Since the output of the Hash function is an integer in the range 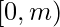 , there are high chances for two strings producing the same hash value.
, there are high chances for two strings producing the same hash value.
For instance, the strings 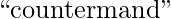 and
and 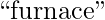 produce the same hash value for
produce the same hash value for 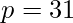 and
and 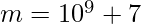 .
.
Also, the strings 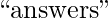 and
and 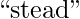 produce the same hash value for
produce the same hash value for 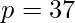 and
and 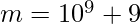 .
.
We can guarantee a collision within a very small domain. Consider a set of strings, 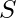 , consisting of only lower-case letters, such that the length of any string in
, consisting of only lower-case letters, such that the length of any string in 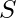 doesn’t exceed
doesn’t exceed 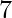 .
.
We have 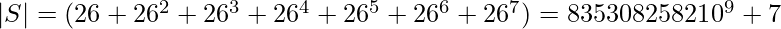 . Since the range of the Hash Function is
. Since the range of the Hash Function is 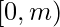 , one-one mapping is impossible. Hence, we can guarantee a collision by arbitrarily generating two strings whose length doesn’t exceed
, one-one mapping is impossible. Hence, we can guarantee a collision by arbitrarily generating two strings whose length doesn’t exceed 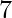 .
.
Collision Resolution
We can note that the value of 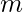 affects the chances of collision. We have seen that the probability of collision is
affects the chances of collision. We have seen that the probability of collision is  . We can increase the value of
. We can increase the value of 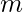 to reduce the probability of collision. But that affects the speed of the algorithm. Larger the value of
to reduce the probability of collision. But that affects the speed of the algorithm. Larger the value of 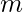 , the slower the algorithm. Also, some languages (C, C++, Java) have a limit on the size of the integer. Hence, we can’t increase the value of
, the slower the algorithm. Also, some languages (C, C++, Java) have a limit on the size of the integer. Hence, we can’t increase the value of 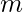 to a very large value.
to a very large value.
Then how can we minimise the chances of a collision?
Note that the hash of a string depends on two parameters: 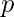 and
and 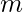 .
.
We have seen that the strings 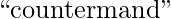 and
and 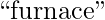 produce the same hash value for
produce the same hash value for 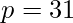 and
and 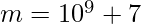 . But for
. But for 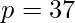 and
and 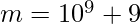 , they produce different hashes.
, they produce different hashes.
Observation:
If two strings produce the same hash values for a pair 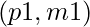 , they will produce different hashes for a different pair,
, they will produce different hashes for a different pair, 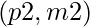 .
.
Strategy:
We cannot, however, nullify the chances of collision because there are infinitely many strings. But, surely, we can reduce the probability of two strings colliding.
We can reduce the probability of collision by generating a pair of hashes for a given string. The first hash is generated using 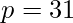 and
and 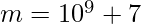 , while the second hash is generated using
, while the second hash is generated using 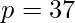 and
and 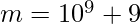 .
.
Why will this work?
We are generating two hashes using two different modulo values, 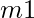 and
and 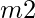 . The probability of a collision is now
. The probability of a collision is now 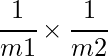 . Since both
. Since both 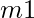 and
and 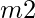 are greater than
are greater than 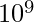 , the probability that a collision occurs is now less than
, the probability that a collision occurs is now less than 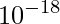 which is so much better than the original probability of collision,
which is so much better than the original probability of collision, 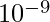 .
.
Below is the implementation for the same
C++
#include <bits/stdc++.h>
using namespace std;
struct Hash {
const int p1 = 31, m1 = 1e9 + 7;
const int p2 = 37, m2 = 1e9 + 9;
int hash1 = 0, hash2 = 0;
Hash(const string& s) {
compute_hash1(s);
compute_hash2(s);
}
void compute_hash1(const string& s) {
long p_pow = 1;
for(char ch: s) {
hash1 = (hash1 + (ch + 1 - 'a') * p_pow) % m1;
p_pow = (p_pow * p1) % m1;
}
}
void compute_hash2(const string& s) {
long p_pow = 1;
for(char ch: s) {
hash2 = (hash2 + (ch + 1 - 'a') * p_pow) % m2;
p_pow = (p_pow * p2) % m2;
}
}
bool operator==(const Hash& other) {
return (hash1 == other.hash1 && hash2 == other.hash2);
}
};
int main() {
const string s = "geeksforgeeks";
Hash h(s);
cout << "Hash values of " << s << " are: ";
cout << "(" << h.hash1 << ", " << h.hash2 << ")" << '\n';
return 0;
}
|
C
#include <stdio.h>
#include <string.h>
int get_hash1(const char* s, int length) {
const int p = 31, m = 1e9 + 7;
int hash_value = 0;
long p_pow = 1;
for(int i = 0; i < length; i++) {
hash_value = (hash_value + (s[i] - 'a' + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
return hash_value;
}
int get_hash2(const char* s, int length) {
const int p = 37, m = 1e9 + 9;
int hash_value = 0;
long p_pow = 1;
for(int i = 0; i < length; i++) {
hash_value = (hash_value + (s[i] - 'a' + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
return hash_value;
}
int main() {
char s[] = "geeksforgeeks";
int length = strlen(s);
int hash1 = get_hash1(s, length);
int hash2 = get_hash2(s, length);
printf("Hash values of %s are: (%d, %d)\n", s, hash1, hash2);
return 0;
}
|
Java
class Hash {
final int p1 = 31, m1 = 1000000007;
final int p2 = 37, m2 = 1000000009;
int hash_value1, hash_value2;
Hash(String s) {
compute_hash1(s);
compute_hash2(s);
}
void compute_hash1(String s) {
int hash_so_far = 0;
final char[] s_array = s.toCharArray();
long p_pow = 1;
final int n = s_array.length;
for (int i = 0; i < n; i++) {
hash_so_far = (int)((hash_so_far + (s_array[i] - 'a' + 1) * p_pow) % m1);
p_pow = (p_pow * p1) % m1;
}
hash_value1 = hash_so_far;
}
void compute_hash2(String s) {
int hash_so_far = 0;
final char[] s_array = s.toCharArray();
long p_pow = 1;
final int n = s_array.length;
for (int i = 0; i < n; i++) {
hash_so_far = (int)((hash_so_far + (s_array[i] - 'a' + 1) * p_pow) % m2);
p_pow = (p_pow * p2) % m2;
}
hash_value2 = hash_so_far;
}
}
class Main {
public static void main(String[] args) {
String s = "geeksforgeeks";
Hash h = new Hash(s);
System.out.println("Hash values of " + s + " are: " + h.hash_value1 + ", " + h.hash_value2);
}
}
|
Python3
class Hash:
def __init__(self, s: str):
self.p1, self.m1 = 31, 10**9 + 7
self.p2, self.m2 = 37, 10**9 + 9
self.hash1, self.hash2 = 0, 0
self.compute_hashes(s)
def compute_hashes(self, s: str):
pow1, pow2 = 1, 1
hash1, hash2 = 0, 0
for ch in s:
seed = 1 + ord(ch) - ord('a')
hash1 = (hash1 + seed * pow1) % self.m1
hash2 = (hash2 + seed * pow2) % self.m2
pow1 = (pow1 * self.p1) % self.m1
pow2 = (pow2 * self.p2) % self.m2
self.hash1, self.hash2 = hash1, hash2
def __eq__(self, other):
return self.hash1 == other.hash1 and self.hash2 == other.hash2
def __str__(self):
return f'({self.hash1}, {self.hash2})'
if __name__ == '__main__':
s = "geeksforgeeks"
hash = Hash(s)
print("Hash of " + s + " is " + str(hash))
|
C#
using System;
class Hash {
readonly int p1 = 31, m1 = 1000000007;
readonly int p2 = 37, m2 = 1000000009;
public int hash_value1, hash_value2;
public Hash(string s) {
compute_hash1(s);
compute_hash2(s);
}
void compute_hash1(string s) {
int hash_so_far = 0;
char[] s_array = s.ToCharArray();
long p_pow = 1;
int n = s_array.Length;
for (int i = 0; i < n; i++) {
hash_so_far = (int)((hash_so_far + (s_array[i] - 'a' + 1) * p_pow) % m1);
p_pow = (p_pow * p1) % m1;
}
hash_value1 = hash_so_far;
}
void compute_hash2(string s) {
int hash_so_far = 0;
char[] s_array = s.ToCharArray();
long p_pow = 1;
int n = s_array.Length;
for (int i = 0; i < n; i++) {
hash_so_far = (int)((hash_so_far + (s_array[i] - 'a' + 1) * p_pow) % m2);
p_pow = (p_pow * p2) % m2;
}
hash_value2 = hash_so_far;
}
}
class Program {
public static void Main(string[] args) {
string s = "geeksforgeeks";
Hash h = new Hash(s);
Console.WriteLine("Hash values of " + s + " are: " + h.hash_value1 + ", " + h.hash_value2);
}
}
|
Javascript
function get_hash1(s, length) {
const p = 31, m = 1e9 + 7;
let hash_value = 0;
let p_pow = 1;
for (let i = 0; i < length; i++) {
hash_value = (hash_value + (s.charCodeAt(i) - 97 + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
return hash_value;
}
function get_hash2(s, length) {
const p = 37, m = 1e9 + 9;
let hash_value = 0;
let p_pow = 1;
for (let i = 0; i < length; i++) {
hash_value = (hash_value + (s.charCodeAt(i) - 97 + 1) * p_pow) % m;
p_pow = (p_pow * p) % m;
}
return hash_value;
}
const s = "geeksforgeeks";
const length = s.length;
const hash1 = get_hash1(s, length);
const hash2 = get_hash2(s, length);
console.log(`Hash values of ${s} are: (${hash1}, ${hash2})`);
|
OutputHash values of geeksforgeeks are: (609871790, 642799661)
Time Complexity: O(N)
Auxiliary Space: O(1)
Features of Polynomial rolling hash function
Calculation of Hashes of any substring of a given string in 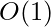
Note that computing the hash of the string S will also compute the hashes of all of the prefixes. We just have to store the hash values of the prefixes while computing. Say \text{hash[i]} denotes the hash of the prefix \text{S[0…i]}, we have
![Rendered by QuickLaTeX.com \text{hash[i...j]}\cdot p^i = \text{hash[0...j]} - \text{hash[0...(i - 1)]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-39059b4e0a5c14bf877b612e1c74da88_l3.png)
This allows us to quickly compute the hash of the substring ![Rendered by QuickLaTeX.com \text{S[i...j]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-96c83b16c33b0c8882e910c8769d0d35_l3.png) in
in 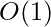 provided we have powers of
provided we have powers of 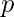 ready.
ready.
The behaviour of the hash when a character is changed
Recall that the hash of a string 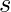 is given by
is given by
![Rendered by QuickLaTeX.com \text{hash(s)} = \displaystyle\sum_{i = 0}^{n - 1} s[i]\cdot p^i\quad \text{mod}\ m](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52c85adb02a08daaea4f4c229eeb62d6_l3.png)
Say, we change a character 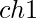 at some index
at some index 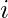 to some other character
to some other character 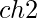 . How will the hash change?
. How will the hash change?
If 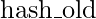 denotes the hash value before changing and
denotes the hash value before changing and 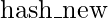 is the hash value after changing, then the relation between them is given by
is the hash value after changing, then the relation between them is given by
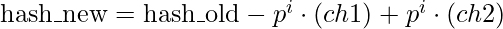
Therefore, queries can be performed very quickly instead of recalculating the hash from beginning, provided we have the powers of 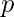 ready.
ready.
A more elegant implementation is provided below.
C++
#include <bits/stdc++.h>
using namespace std;
long long power(long long x, long long y, long long p) {
long long result = 1;
for(; y; y >>= 1, x = x * x % p) {
if(y & 1) {
result = result * x % p;
}
}
return result;
}
long long inverse(long long x, long long p) {
return power(x, p - 2, p);
}
class Hash {
private:
int length;
const int mod1 = 1e9 + 7, mod2 = 1e9 + 9;
const int p1 = 31, p2 = 37;
vector<int> hash1, hash2;
pair<int, int> hash_pair;
public:
inline static vector<int> inv_pow1, inv_pow2;
inline static int inv_size = 1;
Hash() {}
Hash(const string& s) {
length = s.size();
hash1.resize(length);
hash2.resize(length);
int h1 = 0, h2 = 0;
long long p_pow1 = 1, p_pow2 = 1;
for(int i = 0; i < length; i++) {
h1 = (h1 + (s[i] - 'a' + 1) * p_pow1) % mod1;
h2 = (h2 + (s[i] - 'a' + 1) * p_pow2) % mod2;
p_pow1 = (p_pow1 * p1) % mod1;
p_pow2 = (p_pow2 * p2) % mod2;
hash1[i] = h1;
hash2[i] = h2;
}
hash_pair = make_pair(h1, h2);
if(inv_size < length) {
for(; inv_size < length; inv_size <<= 1);
inv_pow1.resize(inv_size, -1);
inv_pow2.resize(inv_size, -1);
inv_pow1[inv_size - 1] = inverse(power(p1, inv_size - 1, mod1), mod1);
inv_pow2[inv_size - 1] = inverse(power(p2, inv_size - 1, mod2), mod2);
for(int i = inv_size - 2; i >= 0 && inv_pow1[i] == -1; i--) {
inv_pow1[i] = (1LL * inv_pow1[i + 1] * p1) % mod1;
inv_pow2[i] = (1LL * inv_pow2[i + 1] * p2) % mod2;
}
}
}
int size() {
return length;
}
pair<int, int> prefix(const int index) {
return {hash1[index], hash2[index]};
}
pair<int, int> substr(const int l, const int r) {
if(l == 0) {
return {hash1[r], hash2[r]};
}
int temp1 = hash1[r] - hash1[l - 1];
int temp2 = hash2[r] - hash2[l - 1];
temp1 += (temp1 < 0 ? mod1 : 0);
temp2 += (temp2 < 0 ? mod2 : 0);
temp1 = (temp1 * 1LL * inv_pow1[l]) % mod1;
temp2 = (temp2 * 1LL * inv_pow2[l]) % mod2;
return {temp1, temp2};
}
bool operator==(const Hash& other) {
return (hash_pair == other.hash_pair);
}
};
int main() {
string my_str = "geeksforgeeks";
const int n = my_str.length();
auto hash = Hash(my_str);
auto hash_pair = hash.substr(0, n - 1);
cout << "Hashes of the string " << my_str << " are:\n";
cout << hash_pair.first << ' ' << hash_pair.second << '\n';
return 0;
}
|
Java
import java.io.*;
public class GFG {
private int length;
private long mod1 = (long) 1e9 + 7;
private long mod2 = (long) 1e9 + 9;
private int p1 = 31;
private int p2 = 37;
private long[] hash1;
private long[] hash2;
public GFG(String s) {
length = s.length();
hash1 = new long[length];
hash2 = new long[length];
long h1 = 0, h2 = 0;
long p_pow1 = 1, p_pow2 = 1;
for (int i = 0; i < length; i++) {
h1 = (h1 + (s.charAt(i) - 'a' + 1) * p_pow1) % mod1;
h2 = (h2 + (s.charAt(i) - 'a' + 1) * p_pow2) % mod2;
p_pow1 = (p_pow1 * p1) % mod1;
p_pow2 = (p_pow2 * p2) % mod2;
hash1[i] = h1;
hash2[i] = h2;
}
}
public Pair<Long, Long> prefix(int index) {
return new Pair<>(hash1[index], hash2[index]);
}
public Pair<Long, Long> substr(int l, int r) {
if (l == 0) {
return new Pair<>(hash1[r], hash2[r]);
}
long temp1 = (hash1[r] - hash1[l - 1] + mod1) % mod1;
long temp2 = (hash2[r] - hash2[l - 1] + mod2) % mod2;
temp1 = (temp1 * modInverse(p1, length - l, mod1)) % mod1;
temp2 = (temp2 * modInverse(p2, length - l, mod2)) % mod2;
return new Pair<>(temp1, temp2);
}
private long modInverse(long base, long exp, long mod) {
long result = 1;
while (exp > 0) {
if (exp % 2 == 1) {
result = (result * base) % mod;
}
base = (base * base) % mod;
exp /= 2;
}
return result;
}
@Override
public boolean equals(Object obj) {
if (this == obj) return true;
if (obj == null || getClass() != obj.getClass()) return false;
GFG other = (GFG) obj;
return prefix(length - 1).equals(other.prefix(other.length - 1));
}
public static void main(String[] args) {
String myStr = "geeksforgeeks";
GFG hash = new GFG(myStr);
Pair<Long, Long> hashPair = hash.substr(0, myStr.length() - 1);
System.out.println("Hashes of the string " + myStr + " are:");
System.out.println(hashPair);
}
}
class Pair<T, U> {
private T first;
private U second;
public Pair(T first, U second) {
this.first = first;
this.second = second;
}
@Override
public String toString() {
return "(" + first + ", " + second + ")";
}
}
|
Python3
class RollingHash:
def __init__(self, s):
self.length = len(s)
self.mod1 = 10**9 + 7
self.mod2 = 10**9 + 9
self.p1 = 31
self.p2 = 37
self.hash1 = [0] * self.length
self.hash2 = [0] * self.length
h1 = h2 = 0
p_pow1 = p_pow2 = 1
for i in range(self.length):
h1 = (h1 + (ord(s[i]) - ord('a') + 1) * p_pow1) % self.mod1
h2 = (h2 + (ord(s[i]) - ord('a') + 1) * p_pow2) % self.mod2
p_pow1 = (p_pow1 * self.p1) % self.mod1
p_pow2 = (p_pow2 * self.p2) % self.mod2
self.hash1[i] = h1
self.hash2[i] = h2
def prefix(self, index):
return (self.hash1[index], self.hash2[index])
def substr(self, l, r):
if l == 0:
return (self.hash1[r], self.hash2[r])
temp1 = self.hash1[r] - self.hash1[l-1]
temp2 = self.hash2[r] - self.hash2[l-1]
temp1 += self.mod1 if temp1 < 0 else 0
temp2 += self.mod2 if temp2 < 0 else 0
temp1 = (temp1 * pow(self.p1, self.length-l, self.mod1)) % self.mod1
temp2 = (temp2 * pow(self.p2, self.length-l, self.mod2)) % self.mod2
return (temp1, temp2)
def __eq__(self, other):
return self.prefix(self.length-1) == other.prefix(other.length-1)
my_str = "geeksforgeeks"
hash = RollingHash(my_str)
hash_pair = hash.substr(0, len(my_str)-1)
print("Hashes of the string", my_str, "are:")
print(hash_pair)
|
C#
using System;
using System.Collections.Generic;
class MainClass
{
static long Power(long x, long y, long p)
{
long result = 1;
while (y > 0)
{
if ((y & 1) == 1)
result = (result * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return result;
}
static long Inverse(long x, long p)
{
return Power(x, p - 2, p);
}
class Hash
{
private int length;
private const int mod1 = 1000000007;
private const int mod2 = 1000000009;
private const int p1 = 31;
private const int p2 = 37;
private List<int> hash1;
private List<int> hash2;
private Tuple<int, int> hashPair;
private static List<int> invPow1;
private static List<int> invPow2;
private static int invSize = 1;
public Hash(string s)
{
length = s.Length;
hash1 = new List<int>(length);
hash2 = new List<int>(length);
int h1 = 0, h2 = 0;
long pPow1 = 1, pPow2 = 1;
for (int i = 0; i < length; i++)
{
h1 = (int)((h1 + (s[i] - 'a' + 1) * pPow1) % mod1);
h2 = (int)((h2 + (s[i] - 'a' + 1) * pPow2) % mod2);
pPow1 = (pPow1 * p1) % mod1;
pPow2 = (pPow2 * p2) % mod2;
hash1.Add(h1);
hash2.Add(h2);
}
hashPair = Tuple.Create(h1, h2);
if (invSize < length)
{
while (invSize < length)
invSize <<= 1;
invPow1 = new List<int>(invSize);
invPow2 = new List<int>(invSize);
for (int i = 0; i < invSize; i++)
{
invPow1.Add(-1);
invPow2.Add(-1);
}
invPow1[invSize - 1] = (int)Inverse(Power(p1, invSize - 1, mod1), mod1);
invPow2[invSize - 1] = (int)Inverse(Power(p2, invSize - 1, mod2), mod2);
for (int i = invSize - 2; i >= 0 && invPow1[i] == -1; i--)
{
invPow1[i] = (int)((1L * invPow1[i + 1] * p1) % mod1);
invPow2[i] = (int)((1L * invPow2[i + 1] * p2) % mod2);
}
}
}
public int Size()
{
return length;
}
public Tuple<int, int> Prefix(int index)
{
return Tuple.Create(hash1[index], hash2[index]);
}
public Tuple<int, int> Substr(int l, int r)
{
if (l == 0)
return Tuple.Create(hash1[r], hash2[r]);
int temp1 = (hash1[r] - hash1[l - 1] + mod1) % mod1;
int temp2 = (hash2[r] - hash2[l - 1] + mod2) % mod2;
temp1 = (int)((1L * temp1 * invPow1[l]) % mod1);
temp2 = (int)((1L * temp2 * invPow2[l]) % mod2);
return Tuple.Create(temp1, temp2);
}
public bool Equals(Hash other)
{
return hashPair.Equals(other.hashPair);
}
}
public static void Main(string[] args)
{
string myStr = "geeksforgeeks";
int n = myStr.Length;
Hash hash = new Hash(myStr);
Tuple<int, int> hashPair = hash.Substr(0, n - 1);
Console.WriteLine("Hashes of the string " + myStr + " are:");
Console.WriteLine(hashPair.Item1 + " " + hashPair.Item2);
}
}
|
Javascript
class Hash {
constructor(s) {
this.length = s.length;
this.mod1 = 1000000007;
this.mod2 = 1000000009;
this.p1 = 31;
this.p2 = 37;
this.hash1 = [];
this.hash2 = [];
let h1 = 0, h2 = 0;
let pPow1 = 1, pPow2 = 1;
for (let i = 0; i < this.length; i++) {
h1 = (h1 + (s.charCodeAt(i) - 'a'.charCodeAt(0) + 1) * pPow1) % this.mod1;
h2 = (h2 + (s.charCodeAt(i) - 'a'.charCodeAt(0) + 1) * pPow2) % this.mod2;
pPow1 = (pPow1 * this.p1) % this.mod1;
pPow2 = (pPow2 * this.p2) % this.mod2;
this.hash1.push(h1);
this.hash2.push(h2);
}
this.hashPair = [h1, h2];
this.invSize = 1;
while (this.invSize < this.length) {
this.invSize <<= 1;
}
this.invPow1 = new Array(this.invSize).fill(-1);
this.invPow2 = new Array(this.invSize).fill(-1);
this.invPow1[this.invSize - 1] = this.inverse(this.power(this.p1, this.invSize - 1, this.mod1), this.mod1);
this.invPow2[this.invSize - 1] = this.inverse(this.power(this.p2, this.invSize - 1, this.mod2), this.mod2);
for (let i = this.invSize - 2; i >= 0 && this.invPow1[i] === -1; i--) {
this.invPow1[i] = (this.invPow1[i + 1] * this.p1) % this.mod1;
this.invPow2[i] = (this.invPow2[i + 1] * this.p2) % this.mod2;
}
}
size() {
return this.length;
}
prefix(index) {
return [this.hash1[index], this.hash2[index]];
}
substr(l, r) {
if (l === 0) {
return [this.hash1[r], this.hash2[r]];
}
let temp1 = (this.hash1[r] - this.hash1[l - 1] + this.mod1) % this.mod1;
let temp2 = (this.hash2[r] - this.hash2[l - 1] + this.mod2) % this.mod2;
temp1 = (temp1 * this.invPow1[l]) % this.mod1;
temp2 = (temp2 * this.invPow2[l]) % this.mod2;
return [temp1, temp2];
}
equals(other) {
return this.hashPair[0] === other.hashPair[0] && this.hashPair[1] === other.hashPair[1];
}
power(x, y, p) {
let result = 1;
while (y > 0) {
if ((y & 1) === 1) {
result = (result * x) % p;
}
y = y >> 1;
x = (x * x) % p;
}
return result;
}
inverse(x, p) {
return this.power(x, p - 2, p);
}
}
const myStr = "geeksforgeeks";
const n = myStr.length;
const hash = new Hash(myStr);
const hashPair = hash.substr(0, n - 1);
console.log("Hashes of the string " + myStr + " are:");
console.log(hashPair[0] + " " + hashPair[1]);
|
In the above implementation, we are computing the inverses of powers of $p$ in linear time.
Applications:
Consider this problem: Given a sequence S of N strings and Q queries. In each query, you are given two indices, i and j, your task is to find the length of the longest common prefix of the strings S[i] and S[j].
Before getting into the approach to solve this problem, note that the constraints are:
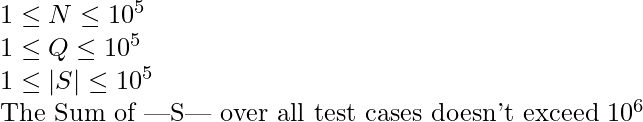
Using Hashing, the problem can be solved in O(N + Q/log|S|_{max}). The approach is to compute hashes for all the strings in O(N) time, Then for each query, we can binary search the length of the longest common prefix using hashing. The implementation for this approach is provided below.
C++14
#include <bits/stdc++.h>
using namespace std;
long long power(long long x, long long y, long long p) {
long long result = 1;
for(; y; y >>= 1, x = x * x % p) {
if(y & 1) {
result = result * x % p;
}
}
return result;
}
long long inverse(long long x, long long p) {
return power(x, p - 2, p);
}
class Hash {
private:
int length;
const int mod1 = 1e9 + 7, mod2 = 1e9 + 9;
const int p1 = 31, p2 = 37;
vector<int> hash1, hash2;
pair<int, int> hash_pair;
public:
inline static vector<int> inv_pow1, inv_pow2;
inline static int inv_size = 1;
Hash() {}
Hash(const string& s) {
length = s.size();
hash1.resize(length);
hash2.resize(length);
int h1 = 0, h2 = 0;
long long p_pow1 = 1, p_pow2 = 1;
for(int i = 0; i < length; i++) {
h1 = (h1 + (s[i] - 'a' + 1) * p_pow1) % mod1;
h2 = (h2 + (s[i] - 'a' + 1) * p_pow2) % mod2;
p_pow1 = (p_pow1 * p1) % mod1;
p_pow2 = (p_pow2 * p2) % mod2;
hash1[i] = h1;
hash2[i] = h2;
}
hash_pair = make_pair(h1, h2);
if(inv_size < length) {
for(; inv_size < length; inv_size <<= 1);
inv_pow1.resize(inv_size, -1);
inv_pow2.resize(inv_size, -1);
inv_pow1[inv_size - 1] = inverse(power(p1, inv_size - 1, mod1), mod1);
inv_pow2[inv_size - 1] = inverse(power(p2, inv_size - 1, mod2), mod2);
for(int i = inv_size - 2; i >= 0 && inv_pow1[i] == -1; i--) {
inv_pow1[i] = (1LL * inv_pow1[i + 1] * p1) % mod1;
inv_pow2[i] = (1LL * inv_pow2[i + 1] * p2) % mod2;
}
}
}
int size() {
return length;
}
pair<int, int> prefix(const int index) {
return {hash1[index], hash2[index]};
}
pair<int, int> substr(const int l, const int r) {
if(l == 0) {
return {hash1[r], hash2[r]};
}
int temp1 = hash1[r] - hash1[l - 1];
int temp2 = hash2[r] - hash2[l - 1];
temp1 += (temp1 < 0 ? mod1 : 0);
temp2 += (temp2 < 0 ? mod2 : 0);
temp1 = (temp1 * 1LL * inv_pow1[l]) % mod1;
temp2 = (temp2 * 1LL * inv_pow2[l]) % mod2;
return {temp1, temp2};
}
bool operator==(const Hash& other) {
return (hash_pair == other.hash_pair);
}
};
void query(vector<Hash>& hashes, const int N) {
int i = 0, j = 0;
cin >> i >> j;
i--, j--;
int lb = 0, ub = min(hashes[i].size(), hashes[j].size());
int max_length = 0;
while(lb <= ub) {
int mid = (lb + ub) >> 1;
if(hashes[i].prefix(mid) == hashes[j].prefix(mid)) {
if(mid + 1 > max_length) {
max_length = mid + 1;
}
lb = mid + 1;
}
else {
ub = mid - 1;
}
}
cout << max_length << '\n';
}
int main() {
int N = 0, Q = 0;
cin >> N >> Q;
vector<Hash> hashes;
for(int i = 0; i < N; i++) {
string s;
cin >> s;
hashes.push_back(Hash(s));
}
for(; Q > 0; Q--) {
query(hashes, N);
}
return 0;
}
|
Input:
5 4
geeksforgeeks geeks hell geeksforpeaks hello
1 2
1 3
3 5
1 4
Expected Output:
5
0
4
8
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...