Class 11 NCERT Solutions- Chapter 15 Statistics – Exercise 15.3
Last Updated :
21 Feb, 2021
Question 1. From the data given below state which group is more variable, A or B?
| Marks | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | 70 – 80 |
| Group A | 9 | 17 | 32 | 33 | 40 | 10 | 9 |
| Group B | 10 | 20 | 30 | 25 | 43 | 15 | 7 |
Solution:
For comparing the variability or dispersion of two series, we calculate the coefficient of variance for each series. The series having greater C.V. is said to be more variable than the other. The series having lesser C.V. is said to be more consistent than the other.
Co-efficient of variation (C.V.) = (σ/ x̅) × 100
Where, σ = standard deviation, x̅ = mean
For Group A
| Marks | Group A (fi) | Mid-point (Xi) | Yi = (xi – A)/h | (Yi)2 | fiyi | fi(yi)2 |
| 10 – 20 | 9 | 15 | ((15 – 45)/10) = -3 | (-3)2 = 9 | -27 | 81 |
| 20 – 30 | 17 | 25 | ((25 – 45)/10) = -2 | (-2)2 = 4 | -34 | 68 |
| 30 – 40 | 32 | 35 | ((35 – 45)/10) = -1 | (-1)2 = 1 | -32 | 32 |
| 40 – 50 | 33 | 45 | ((45 – 45)/10) = 0 | 02 | 0 | 0 |
| 50 – 60 | 40 | 55 | ((55 – 45)/10) = 1 | 12 = 1 | 40 | 40 |
| 60 – 70 | 10 | 65 | ((65 – 45)/10) = 2 | 22 = 4 | 20 | 40 |
| 70 – 80 | 9 | 75 | ((75 – 45)/10) = 3 | 32 = 9 | 27 | 81 |
| Total | 150 | | | | -6 | 342 |
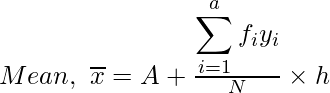
Where A = 45,
and yi = (xi – A)/h
Here h = class size = 20 – 10
h = 10
So, x̅ = 45 + ((-6/150) × 10)
= 45 – 0.4
= 44.6
Then, variance σ2 = ![Rendered by QuickLaTeX.com \frac{h^2}{N^2}[N\sum f_iy_i^2-(\sum f_iy_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a6c29950b201a601731454da0845946c_l3.png)
σ2 = (102/1502) [150(342) – (-6)2]
= (100/22500) [51,300 – 36]
= (100/22500) × 51264
= 227.84
Hence, standard deviation = σ = √227.84
= 15.09
∴ C.V for group A = (σ/ x̅) × 100
= (15.09/44.6) × 100
= 33.83
Now, for group B.
| Marks | Group B (fi) | Mid-point Xi | Yi = (xi – A)/h | (Yi)2 | fiyi | fi(yi)2 |
| 10 – 20 | 10 | 15 | ((15 – 45)/10) = -3 | (-3)2 = 9 | -30 | 90 |
| 20 – 30 | 20 | 25 | ((25 – 45)/10) = -2 | (-2)2 = 4 | -40 | 80 |
| 30 – 40 | 30 | 35 | ((35 – 45)/10) = -1 | (-1)2 = 1 | -30 | 30 |
| 40 – 50 | 25 | 45 | ((45 – 45)/10) = 0 | 02 | 0 | 0 |
| 50 – 60 | 43 | 55 | ((55 – 45)/10) = 1 | 12 = 1 | 43 | 43 |
| 60 – 70 | 15 | 65 | ((65 – 45)/10) = 2 | 22 = 4 | 30 | 60 |
| 70 – 80 | 7 | 75 | ((75 – 45)/10) = 3 | 32 = 9 | 21 | 63 |
| Total | 150 | | | | -6 | 366 |
Mean, 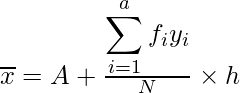
Where A = 45,
h = 10
So, x̅ = 45 + ((-6/150) × 10)
= 45 – 0.4
= 44.6
Then, Variance σ2 = ![Rendered by QuickLaTeX.com \frac{h^2}{N^2}[N\sum f_iy_i^2-(\sum f_iy_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a6c29950b201a601731454da0845946c_l3.png)
σ2 = (102/1502) [150(366) – (-6)2]
= (100/22500) [54,900 – 36]
= (100/22500) × 54,864
= 243.84
Hence, standard deviation = σ = 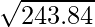
= 15.61
∴ C.V for group B = (σ/ x̅) × 100
= (15.61/44.6) × 100
= 35
By comparing C.V. of group A and group B.
C.V of Group B > C.V. of Group A
So, Group B is more variable.
Question 2. From the prices of shares X and Y below, find out which is more stable in value:
| X | 35 | 54 | 52 | 53 | 56 | 58 | 52 | 50 | 51 | 49 |
| Y | 108 | 107 | 105 | 105 | 106 | 107 | 104 | 103 | 104 | 101 |
Solution:
From the given data,
Let us make the table of the given data and append other columns after calculations.
| X (xi) | Y (yi) | Xi2 | Yi2 |
| 35 | 108 | 1225 | 11664 |
| 54 | 107 | 2916 | 11449 |
| 52 | 105 | 2704 | 11025 |
| 53 | 105 | 2809 | 11025 |
| 56 | 106 | 8136 | 11236 |
| 58 | 107 | 3364 | 11449 |
| 52 | 104 | 2704 | 10816 |
| 50 | 103 | 2500 | 10609 |
| 51 | 104 | 2601 | 10816 |
| 49 | 101 | 26360 | 110290 |
| Total = 510 | 1050 | 26360 | 110290 |
We have to calculate Mean for x,
Mean x̅ = 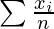
Where, n = number of terms
= 510/10
= 51
Then, Variance for x = ![Rendered by QuickLaTeX.com \frac{1}{n^2}[N\sum x_i^2-(\sum x_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-47fd7b0f7fc17767ab35ac4f79c829e8_l3.png)
= (1/102)[(10 × 26360) – 5102]
= (1/100) (263600 – 260100)
= 3500/100
= 35
WKT Standard deviation = 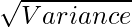
= √35
= 5.91
So, co-efficient of variation = (σ/ x̅) × 100
= (5.91/51) × 100
= 11.58
Now, we have to calculate Mean for y,
Mean 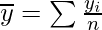
Where, n = number of terms
= 1050/10
= 105
Then, Variance for y = ![Rendered by QuickLaTeX.com \frac{1}{n^2}[N\sum y_i^2-(\sum y_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bb50a919faa3f5c358916af84d06d11d_l3.png)
= (1/102)[(10 × 110290) – 10502]
= (1/100) (1102900 – 1102500)
= 400/100
= 4
WKT Standard deviation = 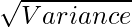
= √4
= 2
So, co-efficient of variation = (σ/ x̅) × 100
= (2/105) × 100
= 1.904
By comparing C.V. of X and Y.
C.V of X > C.V. of Y
So, Y is more stable than X.
Question 3. An analysis of monthly wages paid to workers in two firms A and B, belonging to the same industry, gives the following results:
| | Firm A | Firm B |
| No. of wages earners | 586 | 648 |
| Mean of monthly wages | Rs 5253 | Rs 5253 |
| Variance of the distribution of wages | 100 | 121 |
(i) Which firm A or B pays larger amount as monthly wages?
(ii) Which firm, A or B, shows greater variability in individual wages?
Solution:
(i) From the given table,
Mean monthly wages of firm A = Rs 5253
and Number of wage earners = 586
Then,
Total amount paid = 586 × 5253
= Rs 3078258
Mean monthly wages of firm B = Rs 5253
Number of wage earners = 648
Then,
Total amount paid = 648 × 5253
= Rs 34,03,944
So, firm B pays larger amount as monthly wages.
(ii) Variance of firm A = 100
We know that, standard deviation (σ)= √100
=10
Variance of firm B = 121
Then,
Standard deviation (σ)=√(121 )
=11
Hence the standard deviation is more in case of Firm B that means in firm B there is greater variability in individual wages.
Question 4. The following is the record of goals scored by team A in a football session:
| No. of goals scored | 0 | 1 | 2 | 3 | 4 |
| No. of matches | 1 | 9 | 7 | 5 | 3 |
For the team B, mean number of goals scored per match was 2 with a standard deviation 1.25 goals. Find which team may be considered more consistent?
Solution:
From the given data,
Let us make the table of the given data and append other columns after calculations.
| Number of goals xi | Number of matches fi | fixi | Xi2 | fixi2 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 9 | 9 | 1 | 9 |
| 2 | 7 | 14 | 4 | 28 |
| 3 | 5 | 15 | 9 | 45 |
| Total | 25 | 50 | | 130 |
First we have to calculate Mean for Team A,
Mean = 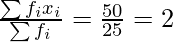
Then,
Variance = ![Rendered by QuickLaTeX.com \frac{1}{N^2}[N\sum f_ix_i^2-(\sum f_ix_i)^2]\\ =\frac{1}{25^2}[25\times130-2500]=\frac{750}{625}=1.2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ff2c5a0fd9d931b63da120d257a80f65_l3.png)
We know that, standard deviation σ = 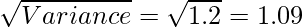
Hence co-efficient of variation of team A,
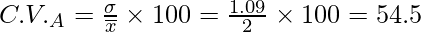
For Team B
Given, x̅ = 2
Standard deviation σ = 1.25
So, coefficient of variation of Team B,
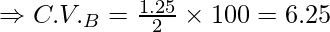
Since C.V. of firm B is greater
∴ Team A is more consistent.
Question 5. The sum and sum of squares corresponding to length x (in cm) and weight y (in gm) of 50 plant products are given below:
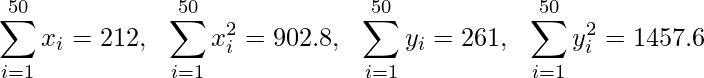
Which is more varying, the length or weight?
Solution:
First we have to calculate Mean for Length x,
Mean = 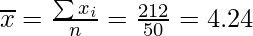
Then,
Variance = ![Rendered by QuickLaTeX.com \frac{1}{N^2}[N\sum f_ix_i^2-(\sum f_ix_i)^2]\\ =\left(\frac{1}{50^2}\right)[(50\times902.8)-212^2]\\ =\left(\frac{1}{2500}\right)(45140-44944)\\ =\frac{196}{2500}\\ =0.0784](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-73a9965e9889249b87737d00391494d6_l3.png)
We know that, standard deviation σ = 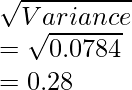
Hence co-efficient of variation of team A,
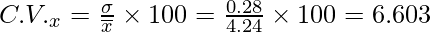
Now we have to calculate mean of weight y
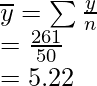
Then,
Variance = ![Rendered by QuickLaTeX.com \left(\frac{1}{N^2}\right)[(N\sum f_iy_i^2)-(\sum f_iy_i)^2]\\ =\left(\frac{1}{50^2}\right)[(50\times1457.6)-261^2]\\ =\left(\frac{1}{2500}\right)(72880-68121)\\ =\frac{4759}{2500}\\ =1.9036](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3fe540ce5c336d6212b137c463de9ea8_l3.png)
When know that, standard deviation σ = 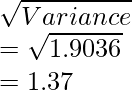
So, co-efficient of variance of Team B,
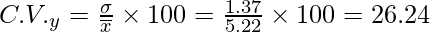
Since C.V. of firm weight y is greater
∴ Weight is more varying.
Share your thoughts in the comments
Please Login to comment...