Class 10 NCERT Solutions- Chapter 14 Statistics – Exercise 14.3
Last Updated :
03 Mar, 2021
Question 1. The following frequency distribution gives the monthly consumption of electricity of 68 consumers in a locality. Find the median, mean, and mode of the data and compare them.
| Monthly consumption(in units) | No. of customers |
| 65-85 | 4 |
| 85-105 | 5 |
| 105-125 | 13 |
| 125-145 | 20 |
| 145-165 | 14 |
| 165-185 | 8 |
| 185-205 | 4 |
Solution:
Total number of consumer n = 68
n/2 =34
So, the median class is 125-145 with cumulative frequency = 42
Here, l = 125, n = 68, Cf = 22, f = 20, h = 20
Now we find the median:
Median = 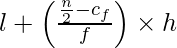
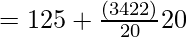
= 125 + 12 = 137
Hence, the median is 137
Now we find the mode:
Modal class = 125 – 145,
Frequencies are
f1 = 20, f0 = 13, f2 = 14 & h = 20
Mode = ![Rendered by QuickLaTeX.com l+ \left[\frac{(f1-f0)}{(2f1-f0-f2)}\right]×h](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ced9e2d4d83d592dbbc70f8d6c6a9f8a_l3.png)
On substituting the values in the given formula, we get
Mode = 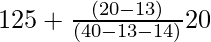
= 125 + 140/13
= 125 + 10.77
= 135.77
Hence, the mode is 135.77
Now we find the mean:
| Class Interval | fi | xi | di = xi – a | ui = di/h | fiui |
| 65-85 | 4 | 75 | -60 | -3 | -12 |
| 85-105 | 5 | 95 | -40 | -2 | -10 |
| 105-125 | 13 | 115 | -20 | -1 | -13 |
| 125-145 | 20 | 135 | 0 | 0 | 0 |
| 145-165 | 14 | 155 | 20 | 1 | 14 |
| 165-185 | 8 | 175 | 40 | 2 | 16 |
| 185-205 | 4 | 195 | 60 | 3 | 12 |
| | Sum fi = 68 | | | | Sum fiui = 7 |
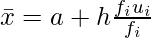
= 135 + 20(7/68)
= 137.05
Hence, the mean is 137.05
Now, on comparing the median, mean, and mode, we found that mean, median and mode are more/less equal in this distribution.
Question 2. If the median of a distribution given below is 28.5 then, find the value of x & y.
| Class Interval | Frequency |
| 0-10 | 5 |
| 10-20 | x |
| 20-30 | 20 |
| 30-40 | 15 |
| 40-50 | y |
| 50-60 | 5 |
| Total | 60 |
Solution:
According to the question
The total number of observations are n = 60
Median of the given data = 28.5
n/2 = 30
Median class is 20 – 30 with a cumulative frequency = 25 + x
Lower limit of median class, l = 20,
Cf = 5 + x,
f = 20 & h = 10
Now we find the median:
Median = 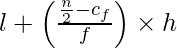
On substituting the values in the given formula, we get
28.5 = 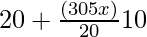
8.5 = (25 – x)/2
17 = 25 – x
Therefore, x = 8
From the cumulative frequency, we can identify the value of x + y as follows:
60 = 5 + 20 + 15 + 5 + x + y
On substituting the values of x, we will find the value of y
60 = 5 + 20 + 15 + 5 + 8 + y
y = 60 – 53
y = 7
So the value of a is 8 and y is 7
Question 3. The Life insurance agent found the following data for the distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to the persons whose age is 18 years onwards but less than the 60 years.
| Age (in years) | Number of policy holder |
| Below 20 | 2 |
| Below 25 | 6 |
| Below 30 | 24 |
| Below 35 | 45 |
| Below 40 | 78 |
| Below 45 | 89 |
| Below 50 | 92 |
| Below 55 | 98 |
| Below 60 | 100 |
Solution:
According to the given question the table is
| Class interval | Frequency | Cumulative frequency |
| 15-20 | 2 | 2 |
| 20-25 | 4 | 6 |
| 25-30 | 18 | 24 |
| 30-35 | 21 | 45 |
| 35-40 | 33 | 78 |
| 40-45 | 11 | 89 |
| 45-50 | 3 | 92 |
| 50-55 | 6 | 98 |
| 55-60 | 2 | 100 |
Given data: n = 100 and n/2 = 50
Median class = 35 – 45
Then, l = 35, cf = 45, f = 33 & h = 5
Now we find the median:
Median = 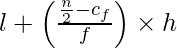
On substituting the values in the given formula, we get
Median = 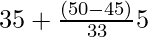
= 35 + 5(5/33)
= 35.75
Hence, the median age is 35.75 years.
Question 4. The lengths of 40 leaves in a plant are measured correctly to the nearest millimeter, and the data obtained is represented as in the following table:
| Length (in mm) | Number of leaves |
| 118-126 | 3 |
| 127-135 | 5 |
| 136-144 | 9 |
| 145-153 | 12 |
| 154-162 | 5 |
| 163-171 | 4 |
| 172-180 | 2 |
Find the median length of leaves.
Solution:
The data in the given table are not continuous to reduce 0.5 in the lower limit and add 0.5 in the upper limit.
We get a new table:
| Class Interval | Frequency | Cumulative frequency |
| 117.5-126.5 | 3 | 3 |
| 126.5-135.5 | 5 | 8 |
| 135.5-144.5 | 9 | 17 |
| 144.5-153.5 | 12 | 29 |
| 153.5-162.5 | 5 | 34 |
| 162.5-171.5 | 4 | 38 |
| 171.5-180.5 | 2 | 40 |
From the given table
n = 40 and n/2 = 20
Median class = 144.5 – 153.5
l = 144.5,
cf = 17, f = 12 & h = 9
Now we find the median:
Median = 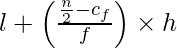
On substituting the values in the given formula, we get
Median = 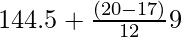
= 144.5 + 9/4
= 146.75 mm
Hence, the median length of the leaves is 146.75 mm.
Question 5. The following table gives the distribution of a life time of 400 neon lamps.
| Lifetime (in hours) | Number of lamps |
| 1500-2000 | 14 |
| 2000-2500 | 56 |
| 2500-3000 | 60 |
| 3000-3500 | 86 |
| 3500-4000 | 74 |
| 4000-4500 | 62 |
| 4500-5000 | 48 |
Find the median lifetime of a lamp.
Solution:
According to the question
| Class Interval | Frequency | Cumulative |
| 1500-2000 | 14 | 14 |
| 2000-2500 | 56 | 70 |
| 2500-3000 | 60 | 130 |
| 3000-3500 | 86 | 216 |
| 3500-4000 | 74 | 290 |
| 4000-4500 | 62 | 352 |
| 4500-5000 | 48 | 400 |
n = 400 and n/2 = 200
Median class = 3000 – 3500
l = 3000, Cf = 130,
f = 86 & h = 500
Now we find the median:
Median = 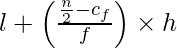
On substituting the values in the given formula, we get
Median = 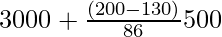
= 3000 + 35000/86 = 3000 + 406.97
= 3406.97
Hence, the median lifetime of the lamps is 3406.97 hours
Question 6. In this 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in English alphabets in the surnames was obtained as follows:
| Number of letters | 1-4 | 4-7 | 7-10 | 10-13 | 13-16 | 16-19 |
| Number of surnames | 6 | 30 | 40 | 16 | 4 | 4 |
Determine the number of median letters in the surnames. Find the number of mean letters in the surnames and also, find the size of modal in the surnames.
Solution:
According to the question
| Class Interval | Frequency | Cumulative Frequency |
| 1-4 | 6 | 6 |
| 4-7 | 30 | 36 |
| 7-10 | 40 | 76 |
| 10-13 | 16 | 92 |
| 13-16 | 4 | 96 |
| 16-19 | 4 | 100 |
n = 100 and n/2 = 50
Median class = 7 – 10
Therefore, l = 7, Cf = 36, f = 40 & h = 3
Now we find the median:
Median = 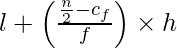
On substituting the values in the given formula, we get
Median = 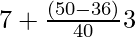
Median = 7 + 42/40 = 8.05
Hence, the median is 8.05
Now we find the mode:
Modal class = 7 – 10,
Where, l = 7, f1 = 40, f0 = 30, f2 = 16 & h = 3
Mode = 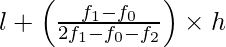
On substituting the values in the given formula, we get
Mode = 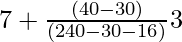
= 7 + 30/34 = 7.88
Hence, the mode is 7.88
Now we find the mean:
| Class Interval | fi | xi | fixi |
| 1-4 | 6 | 2.5 | 15 |
| 4-7 | 30 | 5.5 | 165 |
| 7-10 | 40 | 8.5 | 340 |
| 10-13 | 16 | 11.5 | 184 |
| 13-16 | 4 | 14.5 | 51 |
| 16-19 | 4 | 17.5 | 70 |
| | Sum fi = 100 | | Sum fixi = 825 |
Mean = 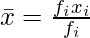
= 825/100 = 8.25
Hence, the mean is 8.25
Question 7. The distributions of below give a weight of 30 students of a class. Find the median weight of a student.
| Weight(in kg) | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 |
| Number of students | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
Solution:
According to the question
| Class Interval | Frequency | Cumulative frequency |
| 40-45 | 2 | 2 |
| 45-50 | 3 | 5 |
| 50-55 | 8 | 13 |
| 55-60 | 6 | 19 |
| 60-65 | 6 | 25 |
| 65-70 | 3 | 28 |
| 70-75 | 2 | 30 |
n = 30 and n/2 = 15
Median class = 55 – 60
l = 55, Cf = 13, f = 6 & h = 5
Now we find the median:
Median = 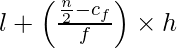
On substituting the values in the given formula, we get
Median = 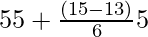
= 55 + 10/6 = 55 + 1.666
= 56.67
Hence, the median weight of the students is 56.67
Share your thoughts in the comments
Please Login to comment...