Class 11 NCERT Solutions- Chapter 9 Sequences And Series – Exercise 9.4
Last Updated :
21 Feb, 2021
Find the sum to n terms of each of the series in Exercises 1 to 7.
Question 1. 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + …
Solution:
Given: Series = 1 × 2 + 2 × 3 + 3 × 4 + 4 × 5 + …
To find nth term, we have
nth term, an = n ( n + 1)
So, the sum of n terms of the series:
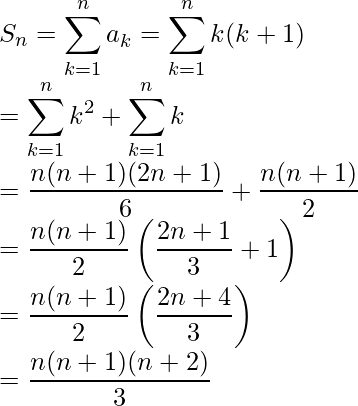
Question 2. 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …
Solution:
Given: Series = 1 × 2 × 3 + 2 × 3 × 4 + 3 × 4 × 5 + …
To find nth term, we have
nth term, an = n(n + 1)(n + 2)
= (n2 + n) (n + 2)
= n3 + 3n2 + 2n
So, the sum of n terms of the series:
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k\\ =\sum^n_{k=1}k^3+3\sum^n_{k=1}k^2+2\sum^n_{k=1}k\\ =\left[\frac{n(n+1)}{2}\right]^2+\frac{3n(n+1)(2n+1)}{6}+\frac{2n(n+1)}{2}\\ =\left[\frac{n(n+1)}{2}\right]^2+\frac{n(n+1)(2n+1)}{2}+n(n+1)\\ =\frac{n(n+1)}{2}\left[\frac{n(n+1)}{2}+2n+1+2\right]\\ =\frac{n(n+1)}{2}\left[\frac{n^2+n+4n+6}{2}\right]\\ =\frac{n(n+1)}{4}(n^2+5n+6)\\ =\frac{n(n+1)}{4}(n^2+2n+3n+6)\\ =\frac{n(n+1)[n(n+2)+3(n+2)]}{4}\\ =\frac{n(n+1)(n+2)(n+3)}{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8e9b2c38d7b601db28225f3529e4b80e_l3.png)
Question 3. 3 × 12 + 5 × 22 + 7 × 32 + …
Solution:
Given: Series = 3 × 12 + 5 × 22 + 7 × 32 + …
To find nth term, we have
nthterm, an = (2n + 1) n2 = 2n3 + n2
So, the sum of n terms of the series:
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k\\ =\sum^n_{k=1}(2k^3+k^2)=2\sum^n_{k=1}k^3+\sum^n_{k=1}k^2\\ =2\left[\frac{n(n+1)}{2}\right]^2+\frac{n(n+1)(2n+1)}{6}\\ =\frac{n^2(n+1)}{2}+\frac{n(n+1)(2n+1)}{6}\\ =\frac{n(n+1)}{2}\left[n(n+1)+\frac{2n+1}{3}\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+3n+2n+1}{3}\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+5n+1}{3}\right]\\ =\frac{n(n+1)(3n^2+5n+1)}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1a96f64a9542c74834a84fce3dd71f0e_l3.png)
Question 4. Find the sum to n terms of the series
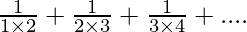
Solution:
Given: Series = 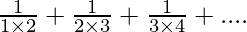
To find nth term, we have
nthterm an =  (By partial fractions)
(By partial fractions)
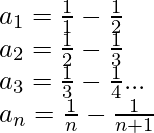
So, on adding the above terms columns wise, we obtain
![Rendered by QuickLaTeX.com a_1+a_2+...+a_n=\left[\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+....\frac{1}{n}\right]-\left[\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...\frac{1}{n+1}\right]\\ \therefore S_n=1-\frac{1}{n+1}=\frac{n+1-1}{n+1}=\frac{n}{n+1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cad6f750b52aec567600cd8b3dcc3a0_l3.png)
Question 5. Find the sum to n terms of the series 52 + 62 + 72 + … + 202
Solution:
Given: Series = 52 + 62 + 72 + … + 202
To find nth term, we have
nth term, an = (n + 4)2 = n2 + 8n + 16
So, the sum of n terms of the series:
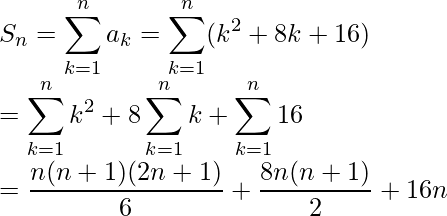
16th term is (16 + 4) = 202
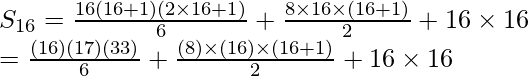
= 1496 + 1088 + 256
= 2840
So, 52 + 62 + 72 + …..+ 202 = 2840
Question 6. Find the sum to n terms of the series 3 × 8 + 6 × 11 + 9 × 14 +…
Solution:
Given: Series = 3 × 8 + 6 × 11 + 9 × 14 + …
To find nth term, we have
an = (nth term of 3, 6, 9 …) × (nth term of 8, 11, 14, …)
= (3n) (3n + 5)
= 9n2 + 15n
So, the sum of n terms of the series:

= 3n(n + 1)(n +3)
Question 7. Find the sum to n terms of the series 12 + (12 + 22) + (12 + 22 + 32) + …
Solution:
Given: Series = 12 + (12 + 22) + (12 + 22 + 32) + …
To find nth term, we have
an = (12 + 22 + 32 +…….+ n2)
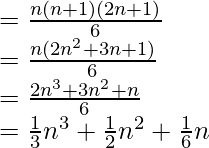
So, the sum of n terms of the series:
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k\\ =\sum^n_{k=1}\left(\frac{1}{3}k^3+\frac{1}{2}k^2+\frac{1}{6}k\right)\\ =\frac{1}{3}\sum^n_{k=1}k^3+\frac{1}{2}\sum^n_{k=1}k^2+\frac{1}{6}\sum^n_{k=1}k\\ =\frac{1}{3}\frac{n^2(n+1)^2}{(2)^2}+\frac{1}{2}\times\frac{n(n+1)(2n+1)}{6}+\frac{1}{6}\times\frac{n(n+1)}{2}\\ =\frac{n(n+1)}{6}\left[\frac{n(n+1)}{2}+\frac{(2n+1)}{2}+\frac{1}{2}\right]\\ =\frac{n(n+1)}{6}\left[\frac{n^2+n+2n+2}{2}\right]\\ =\frac{n(n+1)}{6}\left[\frac{n(n+1)+2(n+1)}{2}\right]\\ =\frac{n(n+1)}{6}\left[\frac{(n+1)(n+2)}{2}\right]\\ =\frac{n(n+1)^2(n+2)}{12}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c3150e8a13505f3a161dee54e8d7820_l3.png)
Question 8. Find the sum to n terms of the series whose nth term is given by n (n + 1) (n + 4).
Solution:
Given: an = n (n + 1) (n + 4) = n(n2 + 5n + 4) = n3 + 5n2 + 4n
Now, the sum of n terms of the series:
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k=\sum^n_{k=1}k^3+5\sum^n_{k=1}k^2+4\sum^n_{k=1}\\ =\frac{n^2(n+1)^2}{4}+\frac{5n(n+1)(2n+1)}{6}+\frac{4n(n+1)}{2}\\ =\frac{n(n+1)}{2}\left[\frac{n(n+1)}{2}+\frac{5(2n+1)}{3}+4\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+3n+20n+10+24}{6}\right]\\ =\frac{n(n+1)}{2}\left[\frac{3n^2+23n+34}{6}\right]\\ =\frac{n(n+1)(3n^2+23n+34)}{12}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f5a0086ea82733475deac1685a8dc486_l3.png)
Question 9. Find the sum to n terms of the series whose nth terms is given by n2 + 2n
Solution:
Given: nth term of the series as:
an = n2 + 2n
So, the sum of n terms of the series:
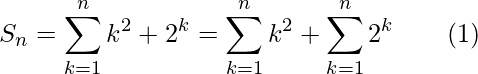
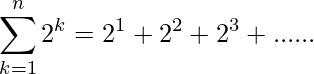
Now, the above series 2, 22, 23 ….. is G.P.
and the first term and common ration is equal to 2.
![Rendered by QuickLaTeX.com \therefore\displaystyle\sum^n_{k=1}2^k=\frac{(2)[(2)^n-1]}{2-1}=2(2^n-1)\ \ \ \ \ (2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-277f7ea037c0a09902ce40e597073c35_l3.png)
From eq(1) and (2), we get
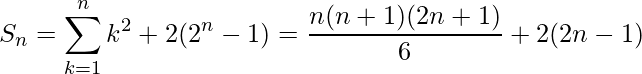
Question 10. Find the sum to n terms of the series whose nth terms is given by (2n – 1)2
Solution:
Given: nthterm of the series as:
an = (2n – 1)2 = 4n2 – 4n + 1
So, the sum of n terms of the series:
![Rendered by QuickLaTeX.com S_n=\displaystyle\sum^n_{k=1}a_k=\sum^n_{k=1}(4k^2-4k+1)\\ =4\sum^n_{k=1}-4\sum^n_{k+1}k+\sum^n_{k=1}1\\ =\frac{4n(n+1)(2n+1)}{6}-\frac{4n(n+1)}{2}+n\\ =\frac{2n(n+1)(2n+1)}{3}-2n(n+1)+n\\ =n\left[\frac{2(2n^2+3n+1)}{3}-2(n+1)+1\right]\\ =n\left[\frac{4n^2+6n+2-6n-6+3}{3}\right]\\ =n\left[\frac{4n^2-1}{3}\right]\\ =\frac{n(2n+1)(2n-1)}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5d020072f8374cbf6a8fe33bcf666c45_l3.png)
Share your thoughts in the comments
Please Login to comment...