Class 10 NCERT Solutions- Chapter 14 Statistics – Exercise 14.2
Last Updated :
03 Mar, 2021
Question 1. The following table shows the ages of the patients admitted in a hospital during a year:
| Age (in years) | 5-15 | 15-25 | 25-35 | 35-45 | 45-55 | 55-65 |
| Number of patients | 6 | 11 | 21 | 23 | 14 | 5 |
Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
Solution:
The greatest frequency in the given table is 23, so the modal class = 35 – 45,
l = 35,
Class width = 10, and the frequencies are
fm = 23, f1 = 21 and f2 = 14
Now, we find the mode using the given formula
Mode = ![Rendered by QuickLaTeX.com l+ \left[\frac{(f_m-f_1)}{(2f_m-f_1-f_2)}\right]×h](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d365f82bb4579a71a7f4a7dbffafe5f_l3.png)
On substituting the values in the formula, we get
Mode = ![Rendered by QuickLaTeX.com 35+\left[\frac{(23-21)}{(46-21-14)}\right]×10](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fe6072398aa833b4f8a9661d183dfba5_l3.png)
= 35 + (20/11) = 35 + 1.8
= 36.8
Hence, the mode of the given data is 36.8 year
Now, we find the mean. So for that first we need to find the midpoint.
xi = (upper limit + lower limit)/2
| Class Interval | Frequency (fi) | Mid-point (xi) | fixi |
| 5-15 | 6 | 10 | 60 |
| 15-25 | 11 | 20 | 220 |
| 25-35 | 21 | 30 | 630 |
| 35-45 | 23 | 40 | 920 |
| 45-55 | 14 | 50 | 700 |
| 55-65 | 5 | 60 | 300 |
| | Sum fi = 80 | | Sum fixi = 2830 |
Mean = 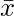 = ∑fixi /∑fi
= ∑fixi /∑fi
= 2830/80
= 35.37 years
Question 2. The following data gives the information on the observed lifetimes (in hours) of 225 electrical components:
| Lifetime (in hours) | 0-20 | 20-40 | 40-60 | 60-80 | 80-100 | 100-120 |
| Frequency | 10 | 35 | 52 | 61 | 38 | 29 |
Determine the modal lifetimes of the components.
Solution:
According to the given question
The modal class is 60 – 80
l = 60, and the frequencies are
fm = 61, f1 = 52, f2 = 38 and h = 20
Now, we find the mode using the given formula
Mode = ![Rendered by QuickLaTeX.com l+ \left[\frac{(f_m-f_1)}{(2f_m-f_1-f_2)}\right]×h](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d365f82bb4579a71a7f4a7dbffafe5f_l3.png)
On substituting the values in the formula, we get
Mode = ![Rendered by QuickLaTeX.com 60+\left[\frac{(61-52)}{(122-52-38)}\right]×20](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db70e888ef784d54c57dc1bd53586c4e_l3.png)
= 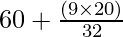
= 60 + 45/8 = 60 + 5.625
Hence, the modal lifetime of the components is 65.625 hours.
Question 3. The following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure:
| Expenditure | Number of families |
| 1000-1500 | 24 |
| 1500-2000 | 40 |
| 2000-2500 | 33 |
| 2500-3000 | 28 |
| 3000-3500 | 30 |
| 3500-4000 | 22 |
| 4000-4500 | 16 |
| 4500-5000 | 7 |
Solution:
According to the question
Modal class = 1500-2000,
l = 1500,and the frequencies are
fm = 40 f1 = 24, f2 = 33 and
h = 500
Now, we find the mode using the given formula
Mode = ![Rendered by QuickLaTeX.com l+ \left[\frac{(f_m-f_1)}{(2f_m-f_1-f_2)}\right]×h](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d365f82bb4579a71a7f4a7dbffafe5f_l3.png)
On substituting the values in the formula, we get
Mode = ![Rendered by QuickLaTeX.com 1500+\left[\frac{(40-24)}{(80-24-33)}\right]×500](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74d540c0ad1a4f13d9fd64fca149f2f5_l3.png)
= 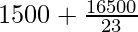
= 1500 + 8000/23 = 1500 + 347.83
So, the modal monthly expenditure of the families is 1847.83 Rupees
Now, we find the mean. So for that first we need to find the midpoint.
xi = (upper limit + lower limit)/2
Let us considered a mean, A be 2750
| Class Interval | fi | xi | di = xi – a | ui = di/h | fiui |
| 1000-1500 | 24 | 1250 | -1500 | -3 | -72 |
| 1500-2000 | 40 | 1750 | -1000 | -2 | -80 |
| 2000-2500 | 33 | 2250 | -500 | -1 | -33 |
| 2500-3000 | 28 | 2750 | 0 | 0 | 0 |
| 3000-3500 | 30 | 3250 | 500 | 1 | 30 |
| 3500-4000 | 22 | 3750 | 1000 | 2 | 44 |
| 4000-4500 | 16 | 4250 | 1500 | 3 | 48 |
| 4500-5000 | 7 | 4750 | 2000 | 4 | 28 |
| | fi = 200 | | | | fiui = -35 |
Mean = 
On substituting the values in the given formula
= 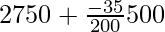
= 2750 – 87.50
= 2662.50
Hence, the mean monthly expenditure of the families is 2662.50 Rupees
Question 4. The following distribution gives the state-wise teacher-student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret the two measures
| No of Students per teacher | Number of states / U.T |
| 15-20 | 3 |
| 20-25 | 8 |
| 25-30 | 9 |
| 30-35 | 10 |
| 35-40 | 3 |
| 40-45 | 0 |
| 45-50 | 0 |
| 50-55 | 2 |
Solution:
According to the question
Modal class = 30 – 35,
l = 30,
Class width (h) = 5, and the frequencies are
fm = 10, f1 = 9 and f2 = 3
Now, we find the mode using the given formula
Mode = ![Rendered by QuickLaTeX.com l+ \left[\frac{(f_m-f_1)}{(2f_m-f_1-f_2)}\right]×h](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d365f82bb4579a71a7f4a7dbffafe5f_l3.png)
On substituting the values in the formula, we get
Mode = 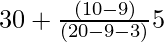
= 30 + 5/8 = 30 + 0.625
= 30.625
Hence, the mode of the given data is 30.625
Now, we find the mean. So for that first we need to find the midpoint.
xi = (upper limit + lower limit)/2
| Class Interval | Frequency (fi) | Mid-point (xi) | fixi |
| 15-20 | 3 | 17.5 | 52.5 |
| 20-25 | 8 | 22.5 | 180.0 |
| 25-30 | 9 | 27.5 | 247.5 |
| 30-35 | 10 | 32.5 | 325.0 |
| 35-40 | 3 | 37.5 | 112.5 |
| 40-45 | 0 | 42.5 | 0 |
| 45-50 | 0 | 47.5 | 0 |
| 50-55 | 2 | 52.5 | 105.5 |
| | Sum fi = 35 | | Sum fixi = 1022.5 |
Mean = 
= 1022.5/35
= 29.2
Hence, the mean is 29.2
Question 5. The given distribution shows the number of runs scored by some top batsmen of the world in one- day international cricket matches.
| Run Scored | Number of Batsman |
| 3000-4000 | 4 |
| 4000-5000 | 18 |
| 5000-6000 | 9 |
| 6000-7000 | 7 |
| 7000-8000 | 6 |
| 8000-9000 | 3 |
| 9000-10000 | 1 |
| 10000-11000 | 1 |
Find the mode of the data.
Solution:
According to the question
Modal class = 4000 – 5000,
l = 4000,
class width (h) = 1000, and the frequencies are
fm = 18, f1 = 4 and f2 = 9
Now, we find the mode using the given formula
Mode = ![Rendered by QuickLaTeX.com l+ \left[\frac{(f_m-f_1)}{(2f_m-f_1-f_2)}\right]×h](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d365f82bb4579a71a7f4a7dbffafe5f_l3.png)
On substituting the values in the formula, we get
Mode = 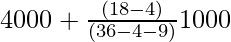
Mode = 4000 + 14000/23 = 4000 + 608.695
= 4608.695
Hence, the mode of the given data is 4608.7 runs
Question 6. A student noted the number of cars passing through a spot on a road for 100 periods each of 3 minutes and summarized it in the table given below. Find the mode of the data:
| Number of cars | Frequency |
| 0-10 | 7 |
| 10-20 | 14 |
| 20-30 | 13 |
| 30-40 | 12 |
| 40-50 | 20 |
| 50-60 | 11 |
| 60-70 | 15 |
| 70-80 | 8 |
Solution:
According to the question
Modal class = 40 – 50, l = 40,
Class width (h) = 10, and the frequencies are
fm = 20, f1 = 12 and f2 = 11
Now, we find the mode using the given formula
Mode = ![Rendered by QuickLaTeX.com l+ \left[\frac{(f_m-f_1)}{(2f_m-f_1-f_2)}\right]×h](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d365f82bb4579a71a7f4a7dbffafe5f_l3.png)
On substituting the values in the formula, we get
Mode = 
Mode = 40 + 80/17 = 40 + 4.7 = 44.7
Hence, the mode of the given data is 44.7 cars
Share your thoughts in the comments
Please Login to comment...